Question

Tangents are drawn to the circles \[{x^2} + {y^2} = 9\] at the points where it is met by the circle \[{x^2} + {y^2} + 3x + 4y + 2 = 0\]. Find the point of intersection of these tangents.

Answer 1

Hint: Draw a suitable diagram of the situation. Use the formula of the equation of the common chord of two circles to form an equation. Similarly use the formula of chord of contact to form another equation for the chord. Use proportionality method to equate the coefficients of the two equations representing the same chord.
* If two circles \[{C_1}\] and \[{C_2}\]intersect and form a common chord then, equation of common chord is given by \[{C_1} - {C_2} = 0\]
* Chord joining the two points of contact from the tangents to the circle from the same external points is called the chord of contact. It is of the form \[T = 0\]. PQ is the chord of contact.

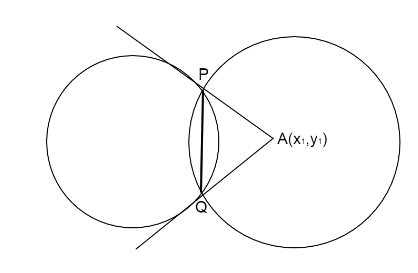
* Chord of contact with respect to point \[({x_1},{y_1})\] of a circle \[{x^2} + {y^2} - {a^2} = 0\] is given by \[x{x_1} + y{y_1} - {a^2} = 0\].

Complete step by step solution:
We draw two intersecting circles \[{C_1}\] and \[{C_2}\] where \[{C_1}:{x^2} + {y^2} = 9;{C_2}:{x^2} + {y^2} + 3x + 4y + 2 = 0\] and \[{C_2}\]. The common chord is PQ that has endpoints joining the tangents to the circle \[{C_1}\].
Equation of circle \[{C_1}:{x^2} + {y^2} - 9 = 0\]............… (1)
Equation of circle \[{C_2}:{x^2} + {y^2} + 3x + 4y + 2 = 0\].............… (2)
Let us assume the point from which the tangents are drawn to the circle \[{C_1}\] as \[(p,q)\].

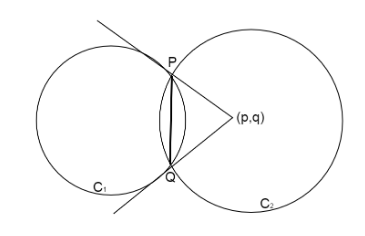
Since PQ is the common chord of two circles \[{C_1},{C_2}\], then the equation of common chord is given by
\[ \Rightarrow {C_1} - {C_2} = 0\]
Substitute the values from equation (1) and (2)
\[ \Rightarrow \left( {{x^2} + {y^2} - 9} \right) - \left( {{x^2} + {y^2} + 3x + 4y + 2} \right) = 0\]
Open the brackets and solve LHS
\[ \Rightarrow {x^2} + {y^2} - 9 - {x^2} - {y^2} - 3x - 4y - 2 = 0\]
Cancel terms with same magnitude and opposite signs
\[ \Rightarrow - 3x - 4y - 11 = 0\]
Multiply -1 to both sides of the equation
\[ \Rightarrow \left( { - 3x - 4y - 11} \right) \times - 1 = 0 \times - 1\]
\[ \Rightarrow 3x + 4y + 11 = 0\]..............… (3)
Now we know the tangents drawn to the circle \[{C_1}\] from the external point \[(p,q)\] form the chord of contact after joining their end points.
Since chord of contact with respect to point \[({x_1},{y_1})\] of a circle \[{x^2} + {y^2} - {a^2} = 0\] is given by \[x{x_1} + y{y_1} - {a^2} = 0\].
So, Chord of contact with respect to point \[(p,q)\] of a circle \[{x^2} + {y^2} - 9 = 0\] is given by \[xp + yq - 9 = 0\].................… (4)
We know both equations (3) and (4) are equations of the same chord PQ
So, their coefficients should be in proportion.
We can write from equations (3) and (4)
\[ \Rightarrow \dfrac{p}{3} = \dfrac{q}{4} = \dfrac{{ - 9}}{{11}}\]
We first equate the first fraction to last fraction:
\[ \Rightarrow \dfrac{p}{3} = \dfrac{{ - 9}}{{11}}\]
Multiply both sides of the equation by 3
\[ \Rightarrow \dfrac{p}{3} \times 3 = \dfrac{{ - 9}}{{11}} \times 3\]
\[ \Rightarrow p = \dfrac{{ - 27}}{{11}}\]
Now we equate the second fraction to last fraction:
\[ \Rightarrow \dfrac{q}{4} = \dfrac{{ - 9}}{{11}}\]
Multiply both sides of the equation by 4
\[ \Rightarrow \dfrac{q}{4} \times 4 = \dfrac{{ - 9}}{{11}} \times 4\]
\[ \Rightarrow q = \dfrac{{ - 36}}{{11}}\]
So, the point \[(p,q) = \left( {\dfrac{{ - 27}}{{11}},\dfrac{{ - 36}}{{11}}} \right)\]

\[\therefore \]Point of intersection of tangents is \[\left( {\dfrac{{ - 27}}{{11}},\dfrac{{ - 36}}{{11}}} \right)\]

Note: Students might get confused while solving the two equations formed in equations (3) and (4) and might try to solve them using other methods like substitution, but we have both the equations of same line, so the equations are either equal or one equation is a multiple of other equation. Keep in mind the equation is solved by substitution method, we will have to find values of ‘x’ and ‘y’ first, then find the values of ‘p’ and ‘q’ which is a long process, so try to avoid it.
Many students might try to solve for the point of intersection of two tangents by using the triangle formed by tangents and chords. But since we are not given anything about the angles formed or any coordinate of the vertex of the triangle formed we should not attempt this method.