Question

The point of concurrency of the angle bisectors of a triangle is known as _______.
A) Incenter
B) Centroid
C) Orthocenter
D) None of these

Answer 1

Hint: We will first write the definitions of Incentre, Centroid and Orthocenter. Then we will look at the data given to us and match it to the options’ definitions. Thus, we will have our answer.

Complete step-by-step answer:
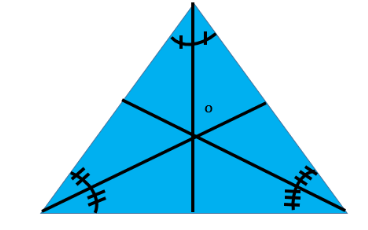
Let us first of all look at the definition of Incentre.
Incenter: In geometry, the incenter of a triangle is a triangle center, a point defined for any triangle in a way that is independent of the triangle's placement or scale. The incenter may be equivalently defined as the point where the internal angle bisectors of the triangle cross, as the point equidistant from the triangle's sides, as the junction point of the medial axis and innermost point of the grassfire transform of the triangle, and as the center point of the inscribed circle of the triangle.
In the following figure, O is the Incenter:

Now, we will see the definition of Centroid.
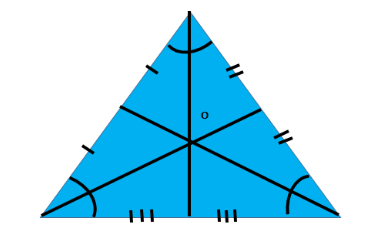
Centroid: The centroid is the center point of the object. The point in which the three medians of the triangle intersect is known as the centroid of a triangle. It is also defined as the point of intersection of all the three medians. The median is a line that joins the midpoint of a side and the opposite vertex of the triangle.
In the following figure, O is the Centroid:

Now, we will see the definition of Orthocenter.
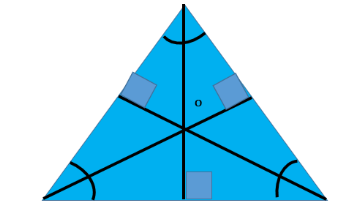
Orthocenter: The orthocenter is the intersecting point for all the altitudes of the triangle. The point where the altitudes of a triangle meet is known as the Orthocenter.
In the following figure, O is the Orthocenter:

Now, in the question it is given that: we need to find the name of the point of concurrency of the angle bisectors of a triangle.
We can clearly see in all the definitions that: the angle bisectors when meet at a point, the point is known as INCENTER.

Hence, the correct option is (A).

Note: The orthocenter is always outside the triangle opposite the longest leg, on the same side as the largest angle. The only time all three of these centers fall in the same spot is in the case of an equilateral triangle. In fact, in this case, the incenter falls in the same place as well.