Question

Two sticks each of length $7\,cm$ are crossing each other such that they bisect each other at right angles. What shape is formed by joining their end points? Give a reason.

Answer 1

Hint:Here, we are given that there are two sticks each of length 7 cm. Now, since the diagonals (sticks) are bisecting each other at right angles, therefore the shape formed by joining their endpoints can be a rhombus or a square. Thus, we will use the diagram to explain the answer and get the final output.

Complete step by step answer:
Given, two sticks each of length 7cm i.e. equal in length. Sticks can be treated as the diagonals of a quadrilateral. Now, since the diagonals (sticks) are bisecting each other at right angles, therefore the shape formed by joining their endpoints can be a rhombus or a square.We will explain this using the figure as below:

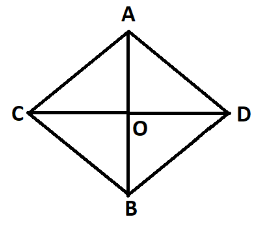
Let AB and CD be the endpoints of sticks. Let sticks intersect at point 0.They bisect each other at right angles.There will be 4 parts formed of sticks.They are A0, OB, CO and OD.
\[AO = OB = CO = OD = 3.5\]
Consider \[\Delta AOD\] and \[\Delta BOD\]
\[ \Rightarrow \angle AOD = \angle BOD = 90^\circ \]
Thus, \[AO = OD = BO\]
\[ \Rightarrow \Delta AOD \cong \Delta BOD\]
\[ \Rightarrow AD = BD\]
Similarly,
\[BC = AC\] and \[AD = BC\]
\[ \Rightarrow AD = BD = BC = AC\]
Thus, all sides are equal. So, the formed figure can be rhombus or square.Both the sticks are of the same length. This means that the diagonals of the quadrilateral formed are equal and also bisect each other perpendicularly.

Note: The key difference between square and rhombus is square has all its angles equal to 90 degrees, but rhombus does not have. The diagonal lengths of a square are of the same measure whereas, of a rhombus they are of different measure. But both the shapes have all their sides as equal. Both are four-sided polygons and a quadrilateral.