NCERT Exemplar for Class 7 Maths Solutions Chapter 6 Triangles

Solved Examples:

1. In the given figure, the side $Q R$ of a $\triangle PQR$ has been produced to the point $S$. If $\angle P R S=$ $115^{\circ}$ and $\angle P=45^{\circ}$, then $\angle Q$ is equal to,

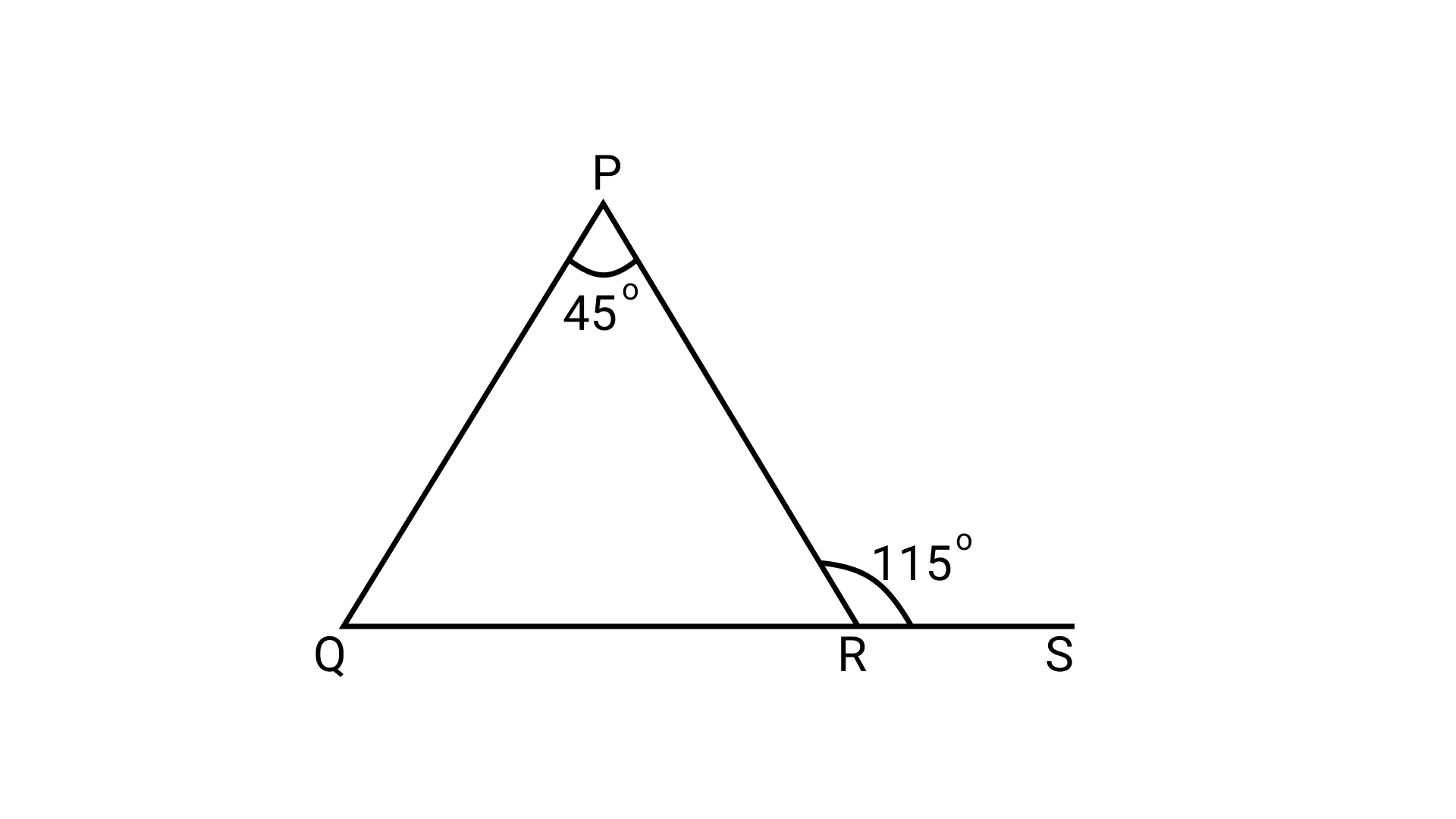
(a) $70^{\circ}$

(b) $105^{\circ}$

(c) $51^{\circ}$

(d) $80^{\circ}$

Ans: Correct answer is (a).

$\angle \mathrm{PRS}=\angle \mathrm{RPQ}+\angle \mathrm{PQR}$ (By exterior angle property)

$\Rightarrow 115^{\circ}=45^{\circ}+\angle P Q R$

$\Rightarrow \angle \mathrm{PQR}=115^{\circ}-45^{\circ}$ $\Rightarrow \angle \mathrm{PQR}=70^{\circ}$

2. In an equilateral triangle ABC (in the given figure), AD is an altitude. Then 4AD2 is equal to

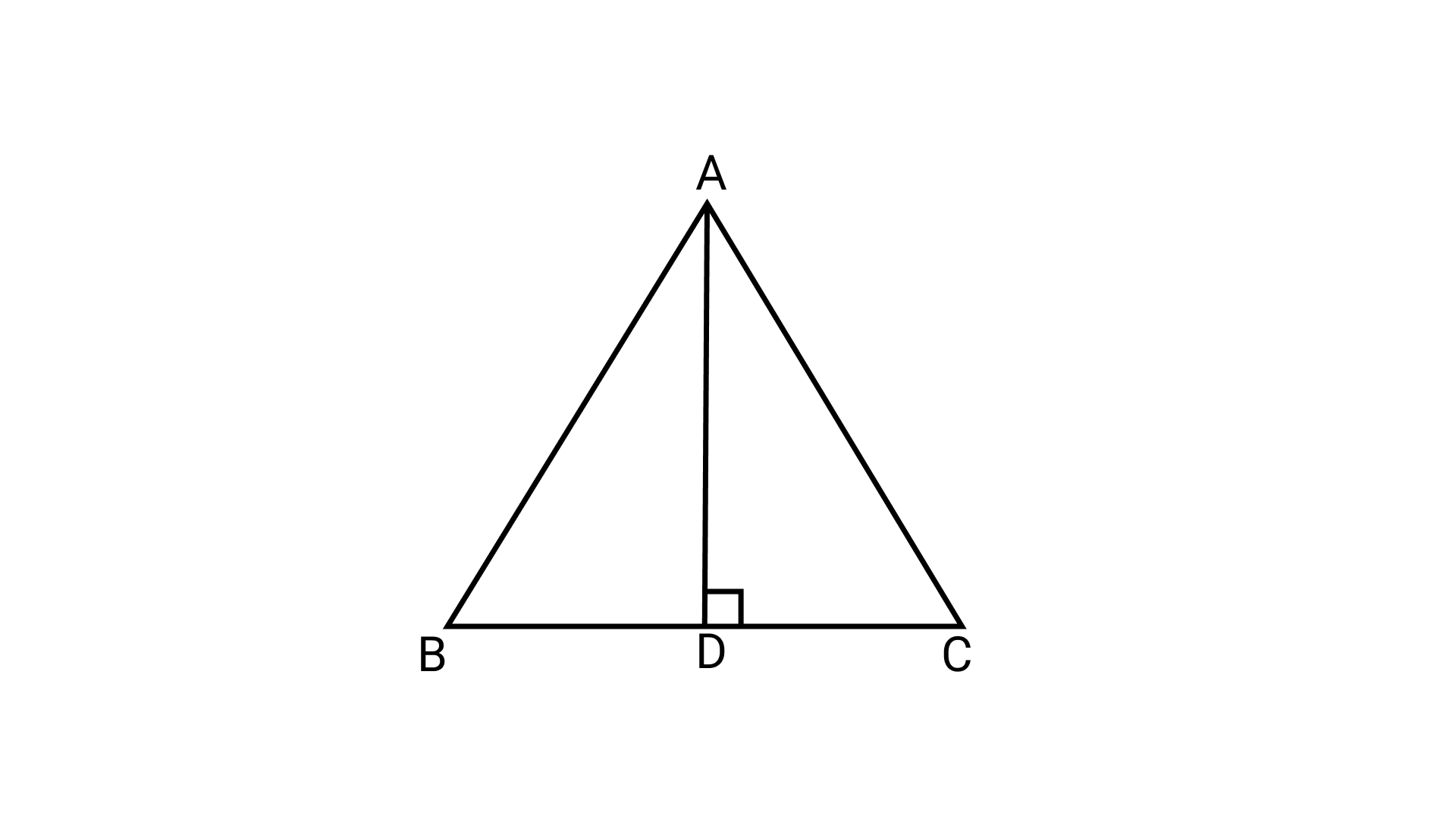
(a) $2 \mathrm{BD}^{2}$

(b) $\mathrm{BC}^{2}$

(c) $3 \mathrm{AB}^{2}$

(d) $2 \mathrm{DC}^{2}$

Ans: Correct answer is (c).

Given AB = BC = AC 

AD is the altitude.

$BD=CD=\dfrac{{AB}}{2}$(in an equivalent triangle AD bisects BC)

Using Pythagoras theorem,

$A{C^2} = A{D^2} + C{D^2}$

$\Rightarrow A{B^2} = A{D^2} + {\left( {\dfrac{{AB}}{2}} \right)^2}$

$\Rightarrow A{D^2} = A{B^2} - \dfrac{{A{B^2}}}{4}$

$\Rightarrow A{D^2} = \dfrac{{3A{B^2}}}{4}$

$\Rightarrow 4A{D^2} = 3A{B^2}$

3. Which of the following cannot be the sides of a triangle?

(a) 3 cm, 4 cm, 5 cm 

(b) 2 cm, 4 cm, 6 cm

(c) 2.5 cm, 3.5 cm, 4.5 cm 

(d) 2.3 cm, 6.4 cm, 5.2 cm

Ans: Correct answer is (b).

It is known that the sum of any two sides of a triangle is always greater than the third side.

In option (b), 2 cm + 4 cm = 6 cm which is equal to 6 cm not greater than 6 cm.

So, sides given in option (b) can not be the sides of a triangle.

4. Which one of the following is not a criterion for congruence of two triangles?

(a) ASA

(b) SSA

(c) SAS

(d) SSS

Ans: Correct answer is (b).

There is no SSA criterion for congruence of two triangles.

5. In the given figure, PS is the bisector of $\angle$P and PQ = PR. Then ∆PRS and ∆PQS are congruent by the criterion

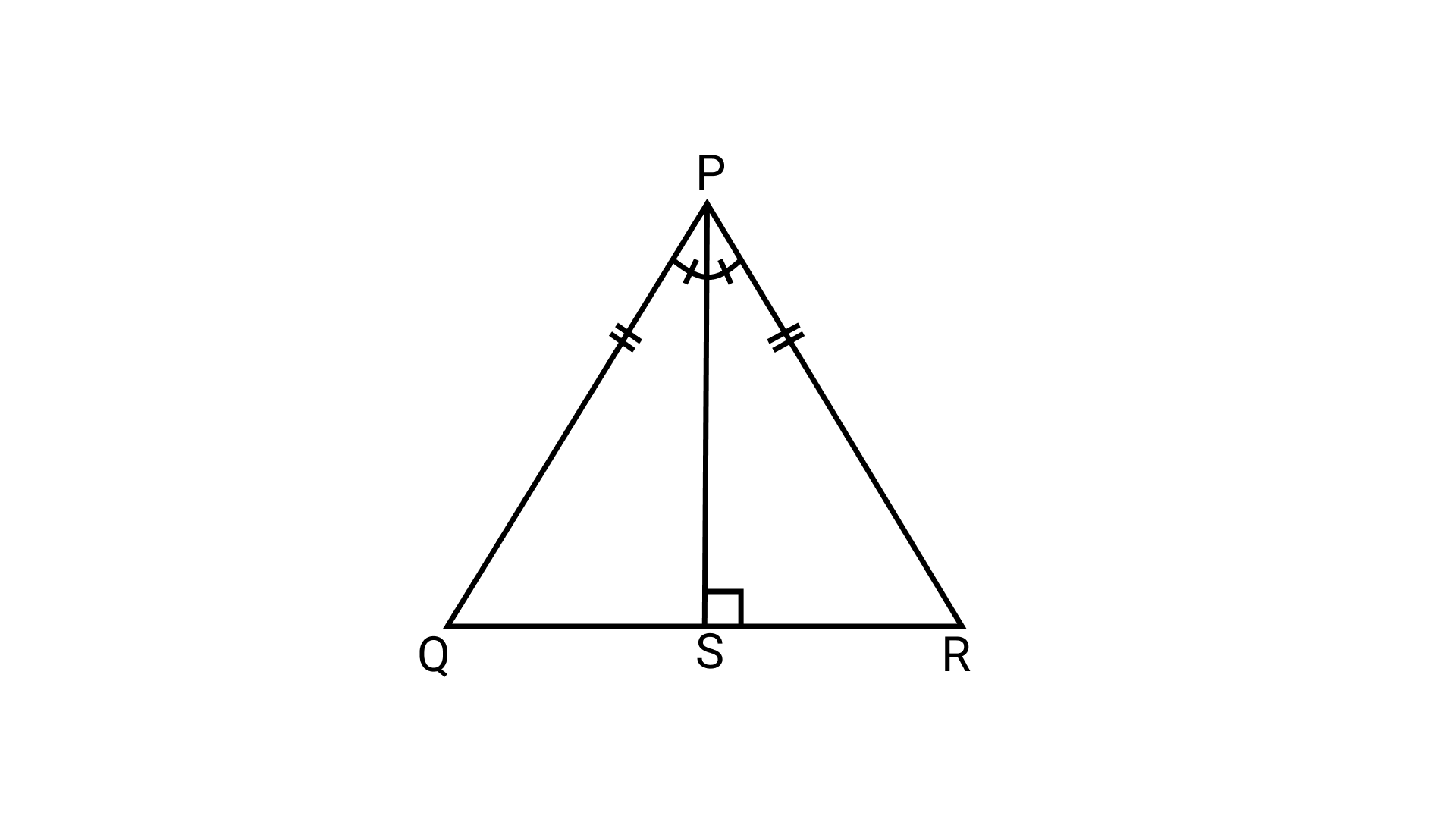
(a) AAA 

(b) SAS 

(c) ASA 

(d) both (b) and (c)

Ans: Correct answer is (b).

PS = PS (common)

$\angle$QPS = $\angle$RPS (Given)

PQ = PR (Given)

So, ∆PRS ≅ ∆PQS (By SAS criterion)

In questions 6 to 9, fill in the blanks to make the statements true.

6. The line segment joining a vertex of a triangle to the mid-point of its opposite side is called its .

Ans: median

7: A triangle is said to be __________, if each one of its sides has the same length.

Ans: equilateral

8: In the given figure, $\angle$ PRS =   $\angle$ QPR + $\angle$_______.

Ans: ∆PQR

By exterior angle property,

$\angle$PRS = $\angle$RPQ + $\angle$PQR

9. Let $A B C$ and $D E F$ be two triangles in which $A B=D E, B C=F D$ and $C A=E F$. The two triangles are congruent under the correspondence $A B C \leftrightarrow$

Ans: $E D F$

Since $A B=D E, B C=F D$ and $C A=E F$,

$\Rightarrow A B C \leftrightarrow E D F$.

In questions 10 to 12, state whether the statements are True or False.

10. Sum of any two sides of a triangle is not less than the third side.

Ans: False

11. The measure of any exterior angle of a triangle is equal to the sum of the measures of its two interior opposite angles.

Ans: True

12. If in ∆ABC and ∆DEF, AB = DE, $\angle$A = $\angle$D and BC = EF then the two triangle ABC and DEF are congruent by SAS criterion.

Ans: False

For triangle to be congruent SAS criterion, it is needed to have two equal sides and the included angle same.

In ΔABC and ΔDFE,

It is given that AB = DE, $\angle$A = $\angle$D, BC = EF

But $\angle$A is formed by the two sides AB and AC of ΔABC and $\angle$D is formed by the two sides DE and EF of $\triangle$ DFE.

So, we need AC = DF for the two triangles to be congruent.

13. In the given figure, find x and y.

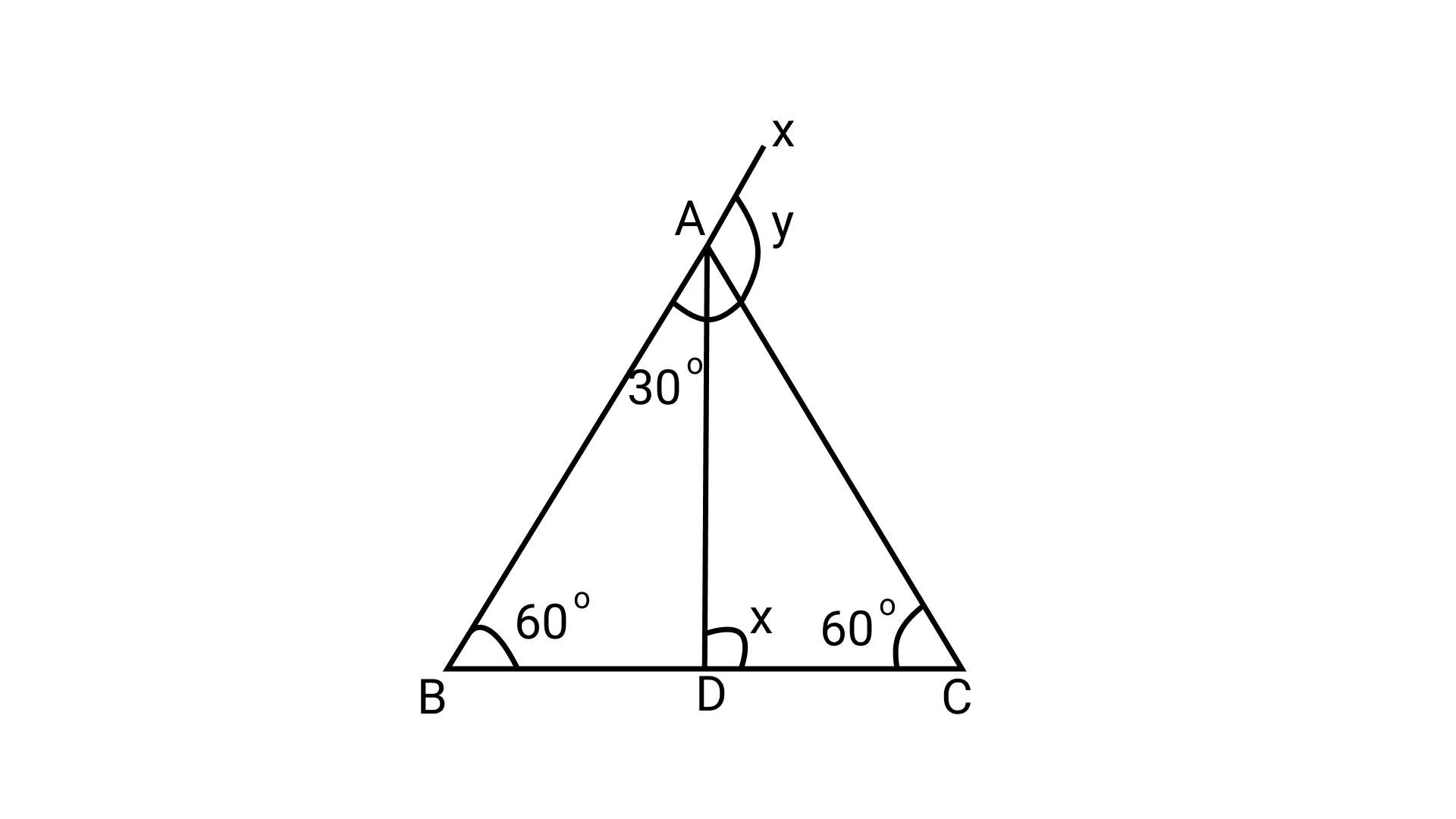
Ans: $\angle$XAC = $\angle$ABD + $\angle$ACB (By exterior angle property)

$y=60^{\circ}+45^{\circ}$ $y=105^{\circ} \ldots \ldots(i)$ In $\triangle A B D$

$\angle$ABD + $\angle$BDA + $\angle$DAB = $x=180^{\circ}$ (By angle sum property)

$x=60^{\circ}$ + BDA + $x=30^{\circ}$ = $x=180^{\circ}$

$\angle$BDA = $x=180^{\circ}$ - $x=60^{\circ}$ - $x=30^{\circ}$

$\angle$BDA = $x=90^{\circ}$

Since BDC is a straight line, $\angle$BDA + x = $x=180^{\circ}$ 

$90^{\circ}+x=180^{\circ}$

$x=90^{\circ}$

Exercise

1. The sides of a triangle have lengths (in cm) 10, 6.5 and a, where a is a whole number. The minimum value that a can take is 

(a) 6 

(b) 5 

(c) 3 

(d) 4 

Ans: Option (d) is correct. 

As we know, the sum of the length of any two sides of a triangle is always more than the length of the third side. 

So

$6.5 + a > 10$

$a > 10 - 6.5$

$a > 3.4$ 

The minimum value of a whole number for $a$ is 4 which is greater than 3.5. 

Therefore, $a = 4$.

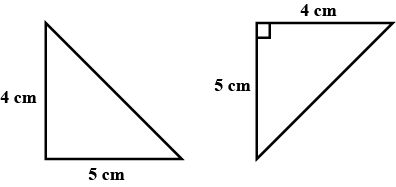
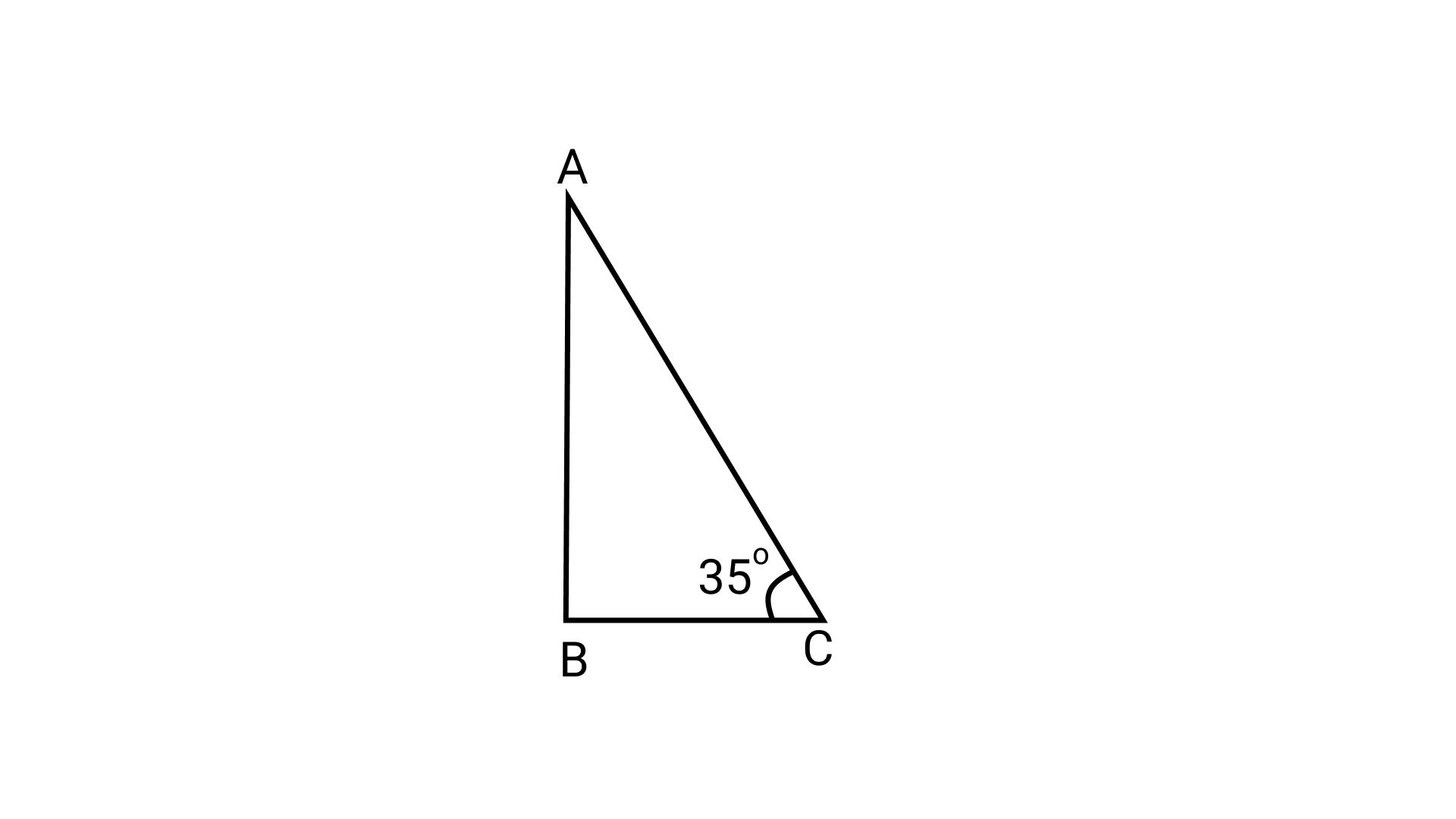
2. Triangle DEF of the given figure is a right triangle with $\angle E=90^{\circ}$.

What type of angles are $\angle D$ and $\angle F$ ?

(a) They are equal angles

(b) They form a pair of adjacent angles

(c) They are complementary angles

(d) They are supplementary angles

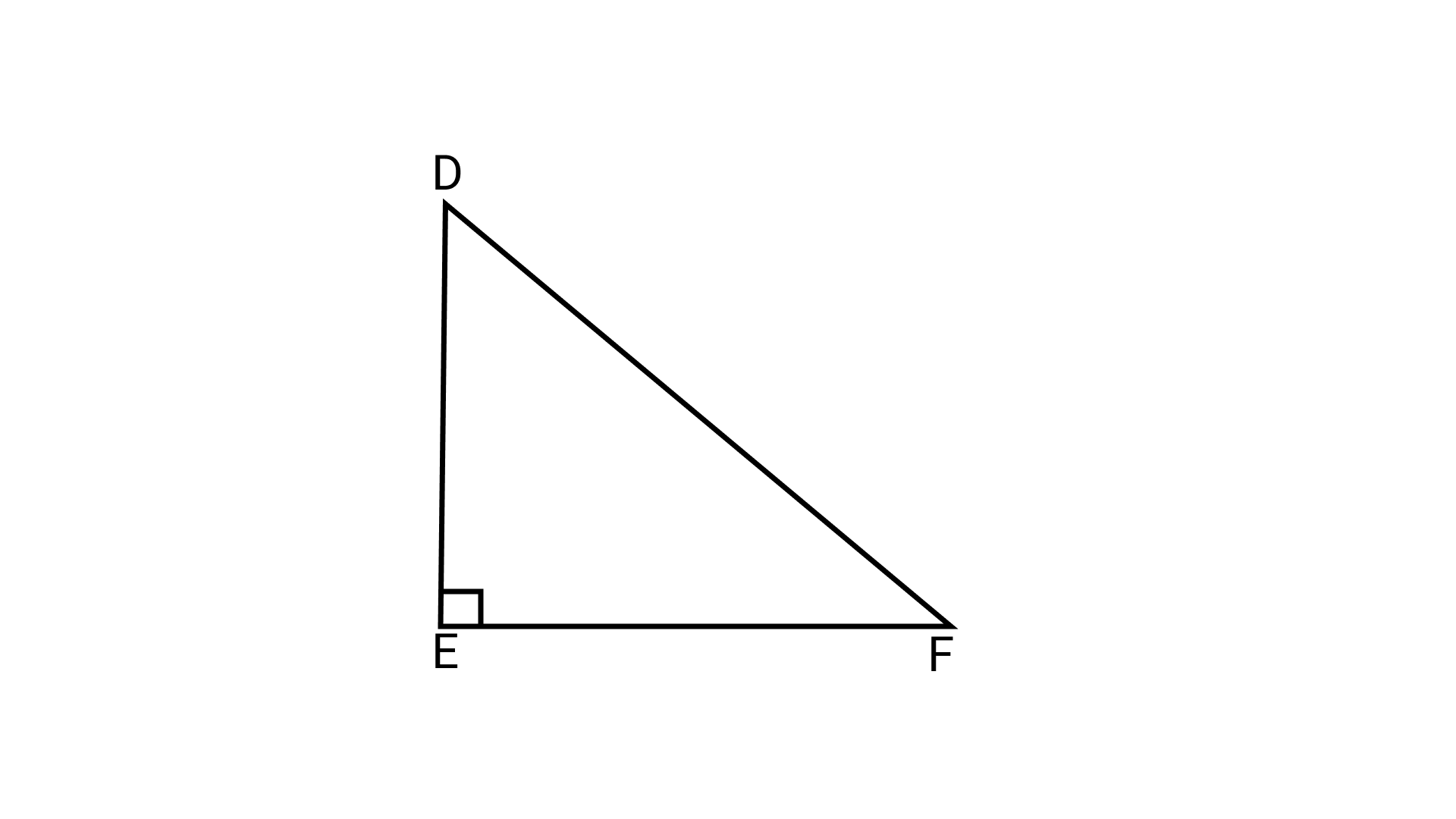
Ans: Option (c) is correct.

By angle sum property of a triangle,

\[\angle D{\text{ }} + \angle E{\text{ }} + \angle F{\text{ }} = {\text{ }}180^\circ \]

Now since  $\angle$ E = $90^\circ$ (given)

$\Rightarrow \angle D{\text{ }} + \angle F{\text{ }} = {\text{ }}180^\circ  - {\text{ }}90^\circ \;$

$= {\text{ }}90^\circ$
Therefore,  $\angle$ D and  $\angle$ F are complementary angles.

3. In the given figure, PQ = PS. The value of x is

(a) $35^\circ$

(b) $45^\circ$

(c) $55^\circ$

(d) $70^\circ$

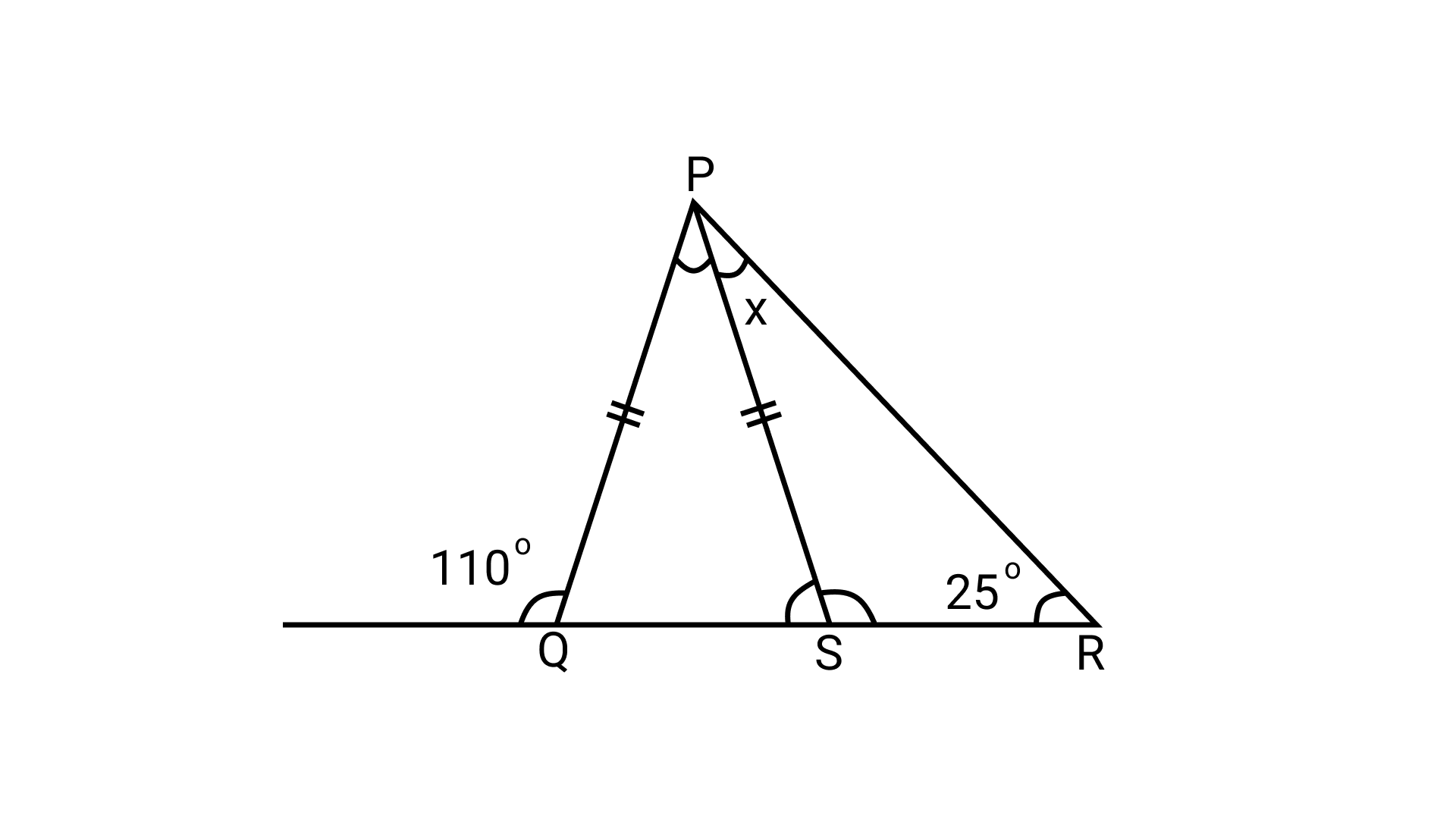
Ans: Option (b) is correct.In △PQS, 

\[\angle 2{\text{ }} + \angle 3{\text{ }} = {\text{ }}110^\circ  \ldots  \ldots \left( {\text{i}} \right)\](Exterior angle property of a triangle)\[\angle 2{\text{ }} + \angle 3{\text{ }} + \angle 4{\text{ }} = {\text{ }}180^\circ \] (Angle sum property of a triangle)

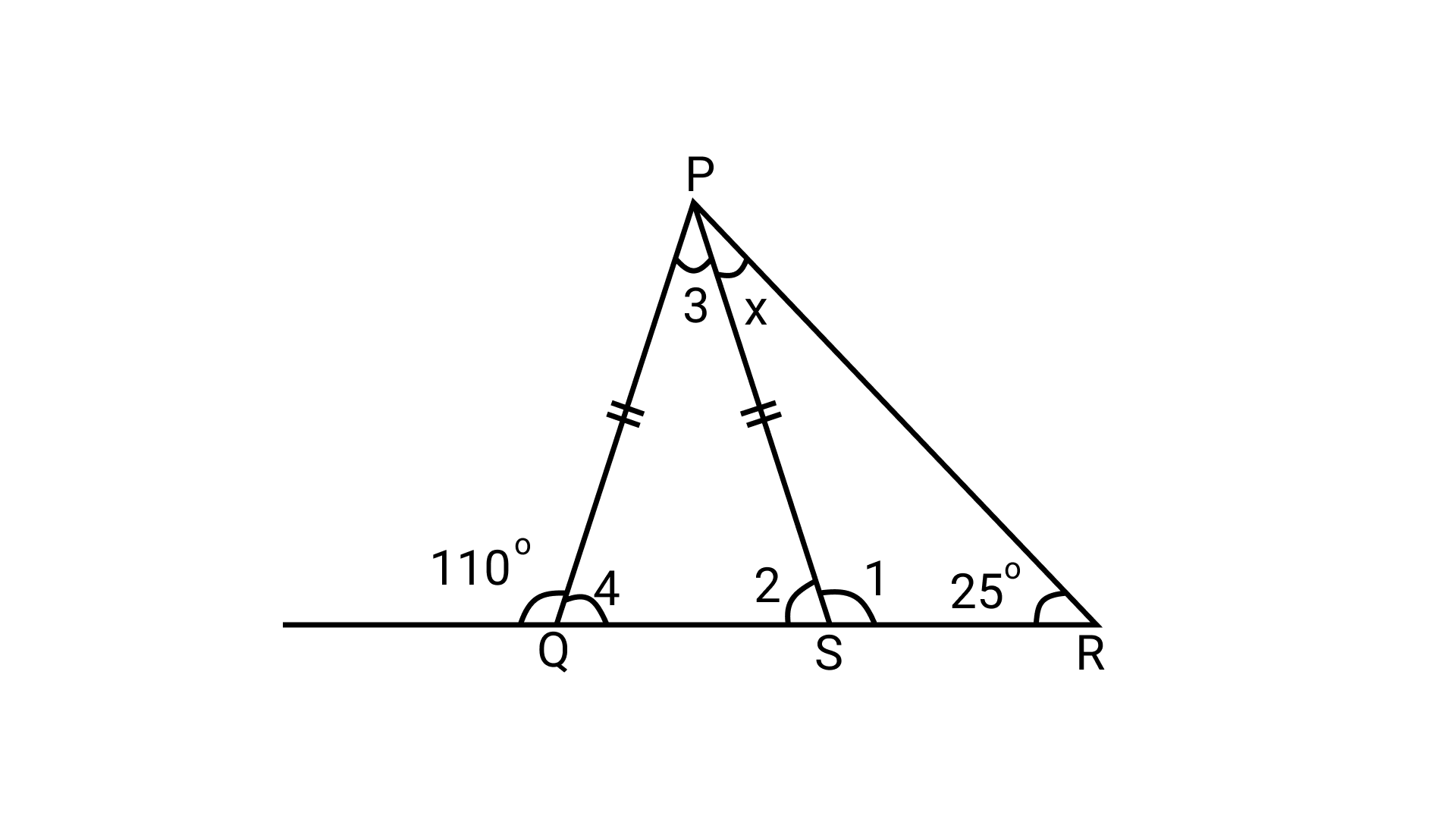
\[\Rightarrow \angle 4{\text{ }} = {\text{ }}180^\circ  - 110^\circ \] (Using equation (i))

\[\Rightarrow \angle 4{\text{ }} = {\text{ }}70^\circ \]

Now, PQ = PS (given)

\[\Rightarrow \angle 2{\text{ }} = \angle 4{\text{ }} = {\text{ }}70^\circ {\text{ }} \ldots  \ldots \left( {{\text{ii}}} \right)\]
Now, in $\triangle$PRS,

\[\angle 2{\text{ }} = {\text{ }}x{\text{ }} + {\text{ }}25^\circ \] (Exterior angle property of a triangle)

\[\Rightarrow x{\text{ }} = {\text{ }}70^\circ -25^\circ \]

\[\Rightarrow x{\text{ }} = {\text{ }}45^\circ \] (Using equation (ii))

4. In a right-angled triangle, the angles other than the right angle are
(a) obtuse

(b) right

(c) acute

(d) straight

Ans: Option (c) is correct.

The sum of angles other than right angle in a right-angled triangle is $90^\circ$
Therefore, both angles other than the right angle must be acute.

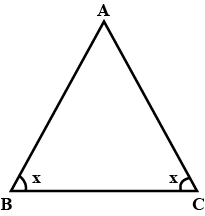
5. In an isosceles triangle, one angle is $70^\circ$. The other two angles are of
(i) $55^\circ$ and $55^\circ$

(ii) $70^\circ$ and $40^\circ$

(iii) any measure

In the given option(s) which of the above statement(s) are true?

(a) (i) only

(b) (ii) only

(c) (iii) only

(d) (i) and (ii)

Ans: Option (d) is correct.

Case 1: 

Let $\triangle$ABC be the given isosceles triangle in which AB = AC and vertex angle is $70^\circ$.
\[\angle 1{\text{ }} = \angle 2 \ldots  \ldots {\text{ }}\left( {\text{i}} \right){\text{ }}[\because {\text{AB  =  AC}}]\]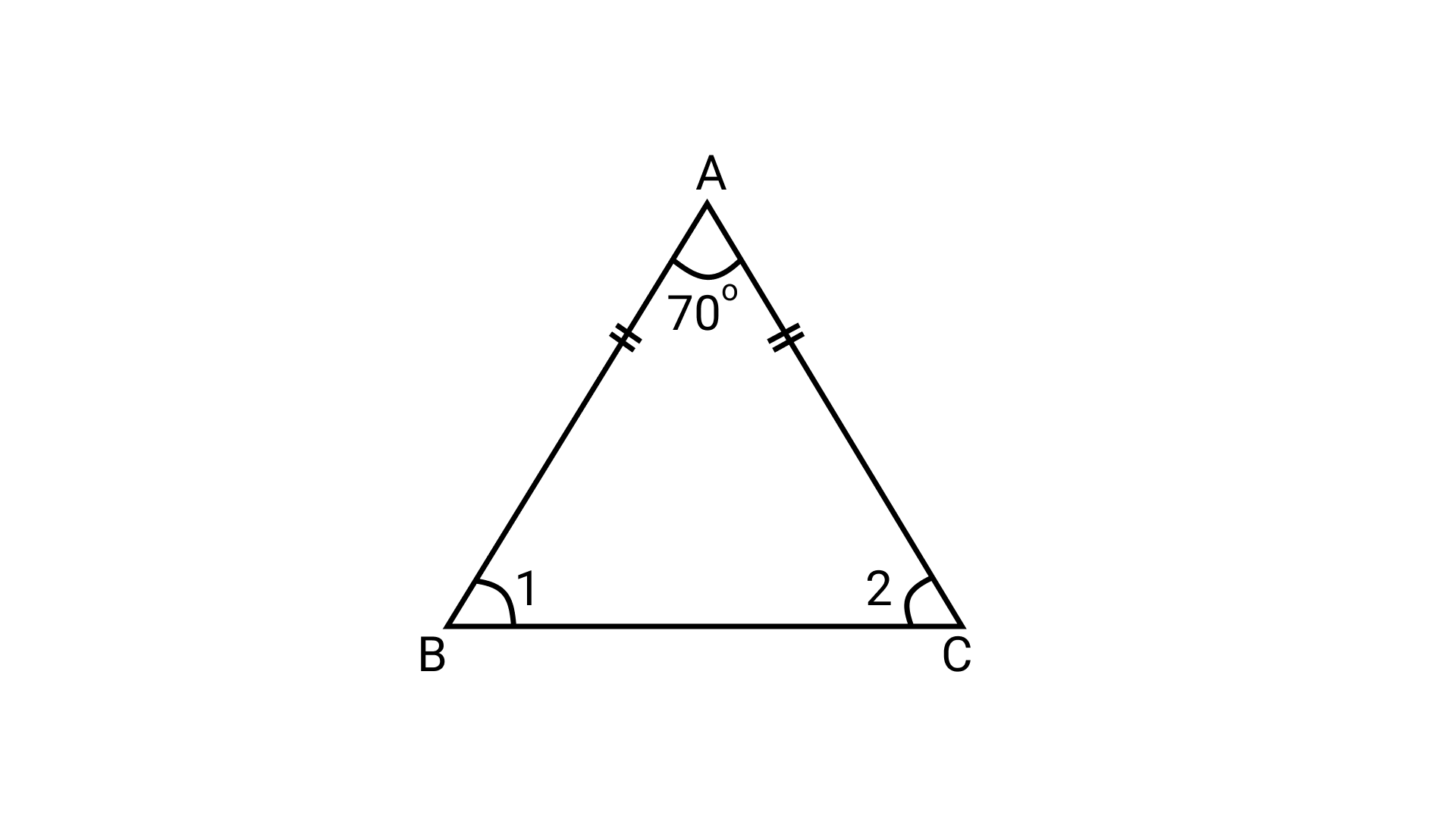

$\angle 1{\text{ }} + \angle 2{\text{ }} + \angle {\text{A }} = {\text{ }}180^\circ \left( {{\text{Angle sum property}}} \right)$

$\Rightarrow 2(\angle 1){\text{ }} = {\text{ }}180^\circ -70^\circ \left( {{\text{Using }}\left( {\text{i}} \right)} \right)$

$\Rightarrow \angle 1 = \frac{{110^\circ }}{2}$

$\Rightarrow \angle 1 = 55^\circ$
Thus, 

\[\angle 1{\text{ }} = \angle 2{\text{ }} = {\text{ }}55^\circ \]
Hence, (i) is true.

Case 2:

Let $\triangle$ABC be the given isosceles triangle in which AB = AC and base angle is $70^\circ$.

\[\angle 2{\text{ }} = {\text{ }}70^\circ [\because {\text{AB  =  AC}}]\]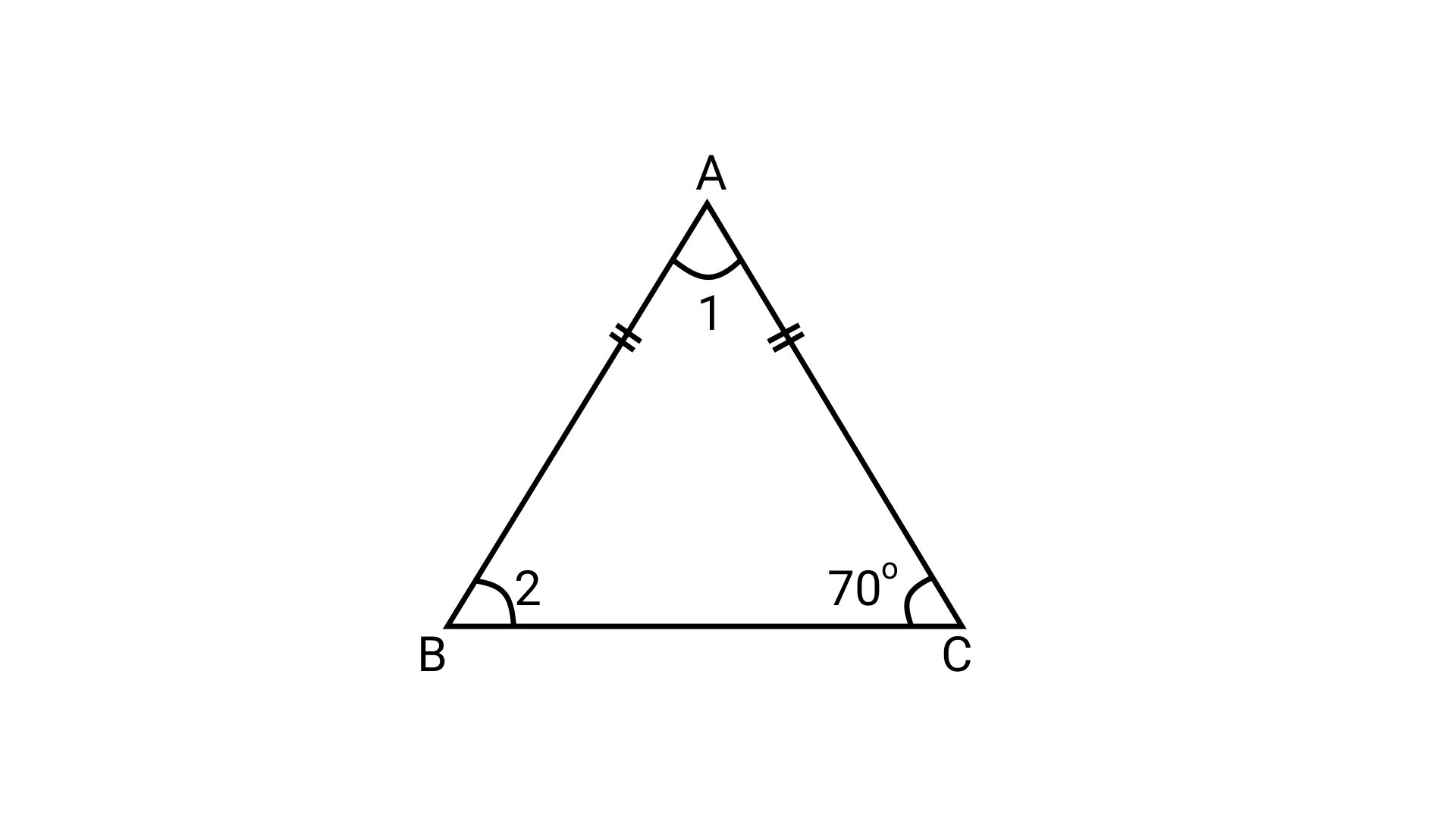

Now, 

$\angle 1{\text{ }} + \angle 2{\text{ }} + \angle C{\text{ }} = {\text{ }}180^\circ$

$\Rightarrow \angle 1{\text{ }} = {\text{ }}180^\circ -70^\circ -70^\circ$

$\Rightarrow \angle 1{\text{ }} = {\text{ }}40^\circ$
Thus, 

\[\angle 1 = {\text{ }}40^\circ \]and \[\angle 2{\text{ }} = {\text{ }}70^\circ \]

Hence, (ii) is also true.

6. In a triangle, one angle is of $90^\circ$. Then

(i) The other two angles are of $45^\circ$ each

(ii) In the remaining two angles, one angle is $90^\circ$ and the other is $45^\circ$

(iii) Remaining two angles are complementary

In the given option(s) which is true?

(a) (i) only

(b) (ii) only

(c) (iii) only

(d) (i) and (ii)

Ans: Option (c) is correct.

In a triangle, if one angle is of $90^\circ$, the remaining two angles are complementary.

7. Lengths of sides of a triangle are 3 cm, 4 cm and 5 cm. The triangle is

(a) Obtuse-angled triangle

(b) Acute-angled triangle

(c) Right-angled triangle

(d) An isosceles right triangle

Ans: Option (c) is correct.

Lengths of sides of a triangle are 3 cm, 4 cm and 5 cm.

Now, 

$\Rightarrow {5^2} = {3^2} + {4^2}$

$\Rightarrow 25 = 9 + 16$

$\Rightarrow 25 = 25$
Here, the sum of squares of two sides is equal to the square of the third side. 

Therefore, a triangle is a right-angled triangle.

8. In the given figure, PB = PD. The value of x is
(a) 85°

(b) $90^\circ$

(c) $25^\circ$

(d) $35^\circ$

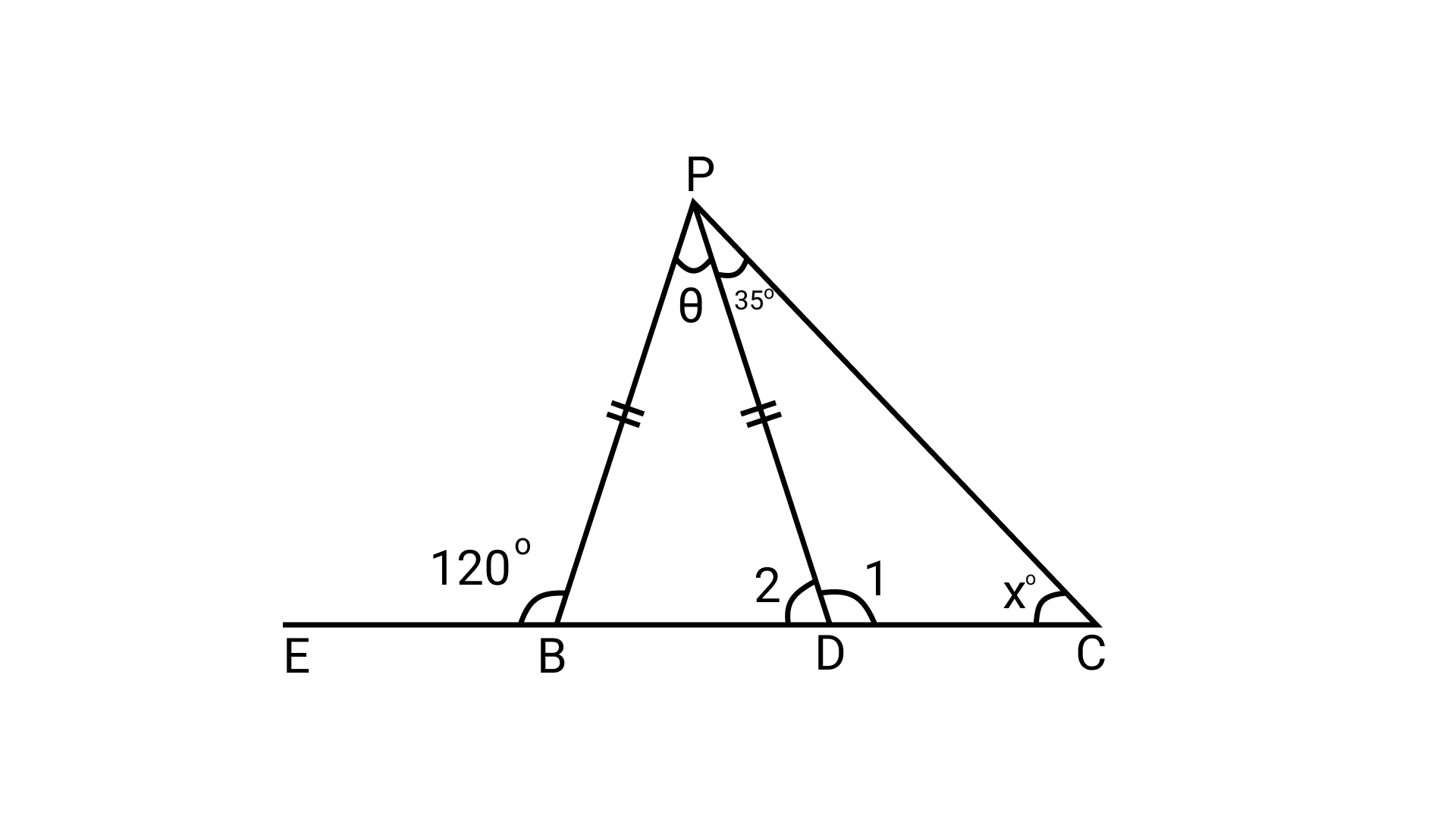
Ans: Option (c) is correct.

\[\angle PBE{\text{ }} = \angle PDB{\text{ }} + \angle BPD\] (Exterior angle property)

\[\Rightarrow 120^\circ  = \angle PDB{\text{ }} + \theta  \ldots  \ldots {\text{ }}\left( {\text{i}} \right)\]

Now, in $\triangle$PBD, 

\[\angle PBD{\text{ }} + \angle BPD{\text{ }} + \angle PDB{\text{ }} = {\text{ }}180^\circ \] (Angle sum property)

$\Rightarrow \angle PBD{\text{ }} + \theta  + \angle PDB{\text{ }} = {\text{ }}180^\circ$

$\Rightarrow \angle PBD{\text{ }} = {\text{ }}180^\circ -120^\circ \left[ {{\text{Using }}\left( {\text{i}} \right)} \right]$

$= {\text{ }}60^\circ$ 

And PB = PD (given)

\[\because \angle PDB{\text{ }} = \angle PBD{\text{ }} = {\text{ }}60^\circ  \ldots  \ldots  \ldots .{\text{ }}\left( {{\text{ii}}} \right)\]

Now, in $\triangle$PDC,

\[\angle PDB{\text{ }} = \angle DCP{\text{ }} + \angle DPC\] (Exterior angle property)

$\Rightarrow 60^\circ  = {\text{ }}x{\text{ }} + {\text{ }}35^\circ \left[ {{\text{Using }}\left( {{\text{ii}}} \right)} \right][\because \angle DCP{\text{ }} = {\text{ }}x,\angle DPC{\text{ }} = {\text{ }}35^\circ \left( {{\text{given}}} \right)]$

$\Rightarrow x{\text{ }} = {\text{ }}60^\circ -35^\circ$

$\Rightarrow x{\text{ }} = {\text{ }}25^\circ$ 

9. In $\triangle$PQR,

(a) PQ – QR > PR

(b) PQ + QR < PR

(c) PQ – QR < PR

(d) PQ + PR < QR 

Ans: Option (c) is correct.

\[\because \] Sum of any two sides of a triangle is greater than the third side.

In a $\triangle$PQR, 

${\Rightarrow PQ{\text{ }} + QR{\text{ }} > PR}$ 

${\Rightarrow QR{\text{ }} + {\text{ }}PR{\text{ }} > {\text{ }}PQ} $

$\Rightarrow PR{\text{ }} + {\text{ }}PQ{\text{ }} > {\text{ }}QR$
And

\[\because \] Difference of any two sides of a triangle is less than the third side

$\Rightarrow PQ-QR{\text{ }} < {\text{ }}PR$

$\Rightarrow QR-PR{\text{ }} < {\text{ }}PQ$

$\Rightarrow PR-PQ{\text{ }} < {\text{ }}QR$ 

10. In $\triangle \mathrm{ABC}$,

(a) AB + BC > AC

(b) AB +BC < AC

(c) AB + AC < BC

(d) AC + BC < AB

Ans: Option (a) is correct.

\[\because \] Sum of any two sides of a triangle is greater than the third side.

In a $\triangle \mathrm{ABC}$, 

$\Rightarrow AB{\text{ }} + {\text{ }}BC{\text{ }} > {\text{ }}AC$

$\Rightarrow BC{\text{ }} + {\text{ }}AC{\text{ }} > {\text{ }}AB$

$\Rightarrow AC{\text{ }} + {\text{ }}AB{\text{ }} > {\text{ }}BC$

11. The top of a broken tree touches the ground at a distance of 12 m from its base. If the tree is broken at a height of 5 m from the ground then the actual height of the tree is:

(a) 25 m

(b) 13 m

(c) 18 m

(d) 17 m

Ans: Option (c) is correct.

Let BC is the broken part of the tree and AB is the unbroken part of the tree.

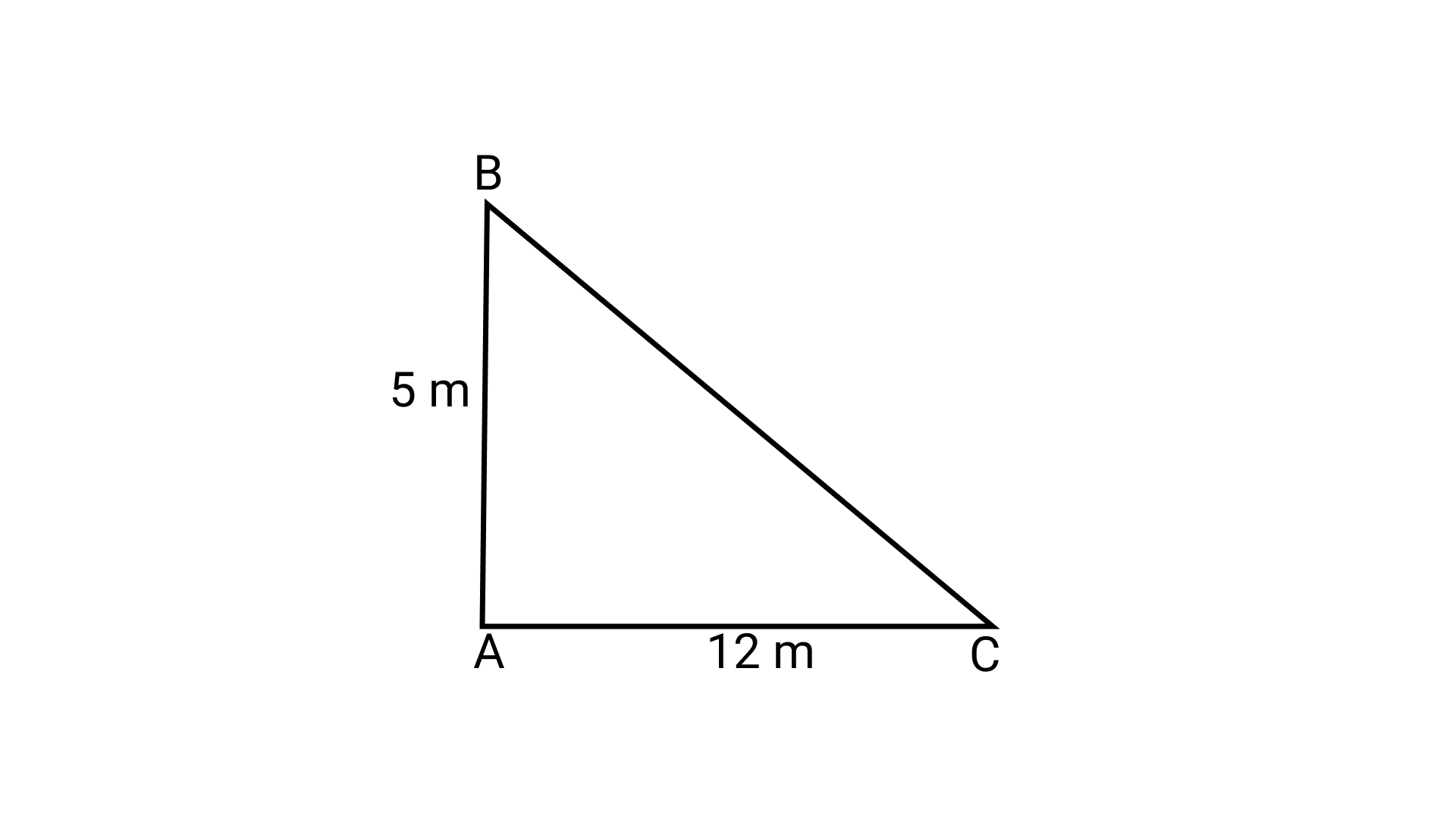
Here, $\triangle \mathrm{ABC}$ is right angled triangle

${\left( {BC} \right)^2}\; = {\text{ }}{\left( {AB} \right)^2}\; + {\text{ }}{\left( {AC} \right)^2}$

$\Rightarrow {\left( {BC} \right)^2}\; = {\text{ }}{\left( 5 \right)^2}\; + {\text{ }}{\left( {12} \right)^2}$

$\Rightarrow {\left( {BC} \right)^2}\; = {\text{ }}25{\text{ }} + {\text{ }}144{\text{ }}$

$\Rightarrow {\left( {BC} \right)^2} = {\text{ }}169$

$\Rightarrow {\left( {BC} \right)^2}\; = {\text{ }}{13^2}$

$\Rightarrow BC{\text{ }} = {\text{ }}13{\text{ m}}$
\[\therefore \] Actual height of tree is \[AB{\text{ }} + {\text{ }}BC{\text{ }} = {\text{ }}\left( {5{\text{ }} + {\text{ }}13} \right){\text{ m }} = {\text{ }}18{\text{ m}}\]

12. The triangle ABC formed by AB = 5 cm, BC = 8 cm, AC = 4 cm is

(a) an isosceles triangle only

(b) a scalene triangle only

(c) an isosceles right triangle

(d) scalene as well as a right triangle

Ans: Option (b) is correct.

AB = 5 cm, BC = 8 cm, AC = 4 cm

Now, 

$\Rightarrow {5^2} + {4^2} \ne {8^2}$

$\Rightarrow 41 \ne 64$
And all sides are unequal.

Therefore, $\triangle \mathrm{ABC}$ is a scalene triangle only.

13. Two trees 7 m and 4 m high stand upright on the ground. If their bases (roots) are 4 m apart, then the distance between their tops is

(a) 3 m                                                                  

(b) 5 m

(c) 4 m                                                                   

(d) 11 m

Ans: Option (b) is correct.

Let AB and CD are the given trees of height 7 m and 4 m respectively.
$AC{\text{ }} = {\text{ }}DE{\text{ }} = {\text{ }}4{\text{ m}}$

$BE{\text{ }} = {\text{ }}AB{\text{ }}-{\text{ }}AE{\text{ }} = {\text{ }}\left( {7{\text{ }}-{\text{ }}4} \right){\text{ m }} = {\text{ }}3{\text{ m }}(\because AE{\text{ }} = {\text{ }}CD{\text{ }} = {\text{ }}4{\text{ m}})$ 

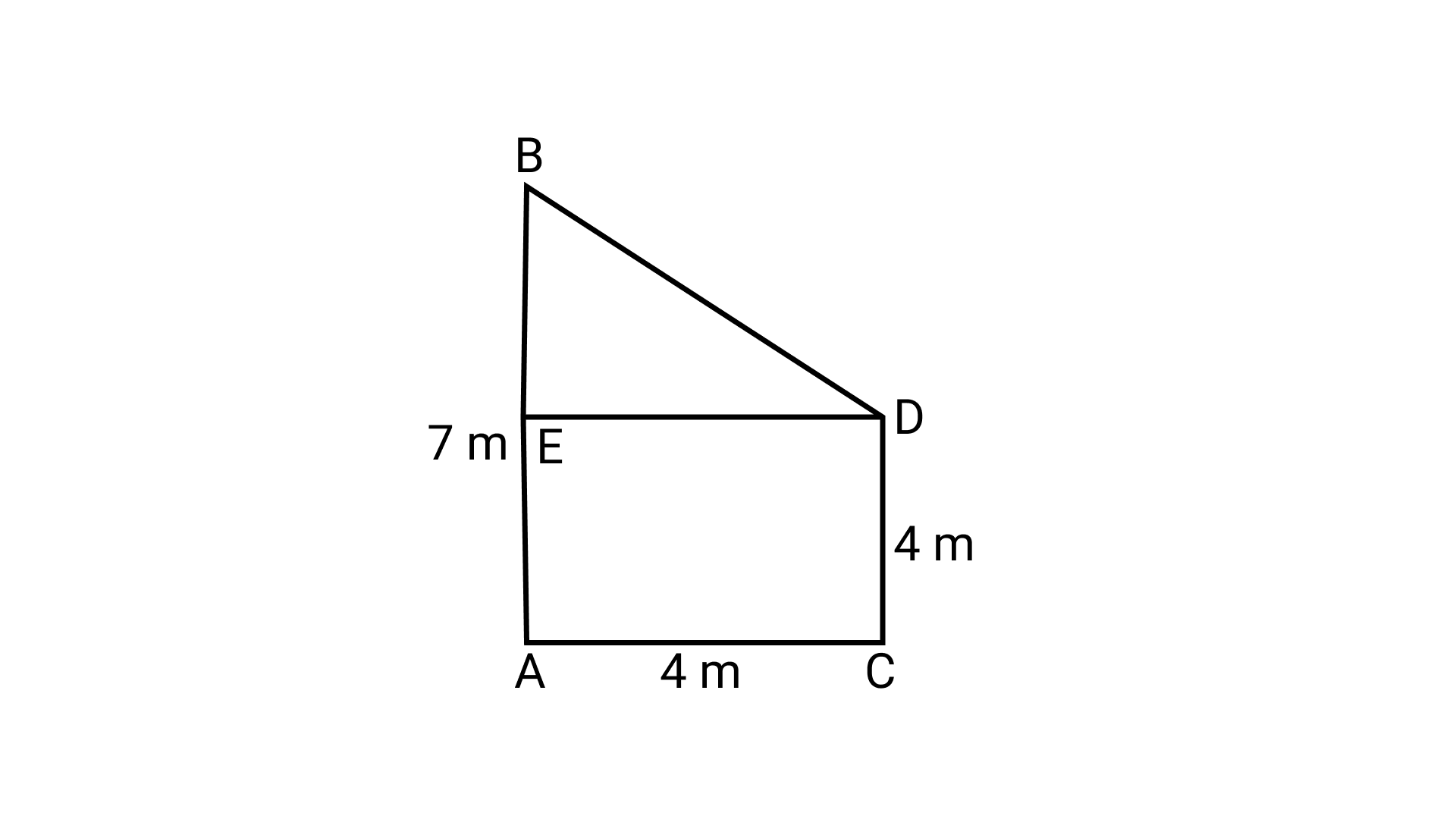
Now, $\triangle$BED is a right-angled triangle.

$\therefore {\left( {BD} \right)^2}\; = {\text{ }}{\left( {BE} \right)^2}\; + {\text{ }}{\left( {DE} \right)^2}$

$\Rightarrow {\left( {BD} \right)^2}\; = {\text{ }}{\left( 3 \right)^2}\; + {\text{ }}{\left( 4 \right)^2}\;$

$\Rightarrow {\left( {BD} \right)^2}\; = {\text{ }}9{\text{ }} + {\text{ }}16$

$\Rightarrow {\left( {BD} \right)^2}\; = {\text{ }}25{\text{ }}$

$\Rightarrow {\left( {BD} \right)^2}\; = {\text{ }}{5^2}$

$\Rightarrow BD{\text{ }} = {\text{ }}5{\text{ m}}$
Hence, the distance between the tops of trees is 5 m.

14. If in an isosceles triangle, each of the base angles is $40^\circ$, then the triangle is

(a) Right – angled triangle

(b) Acute angled triangle

(c) Obtuse-angled triangle

(d) Isosceles right-angled triangle

Ans: Option (c) is correct.

Let $\triangle \mathrm{ABC}$ be the given isosceles triangle in which AB = AC and each base angle is $40^\circ$.

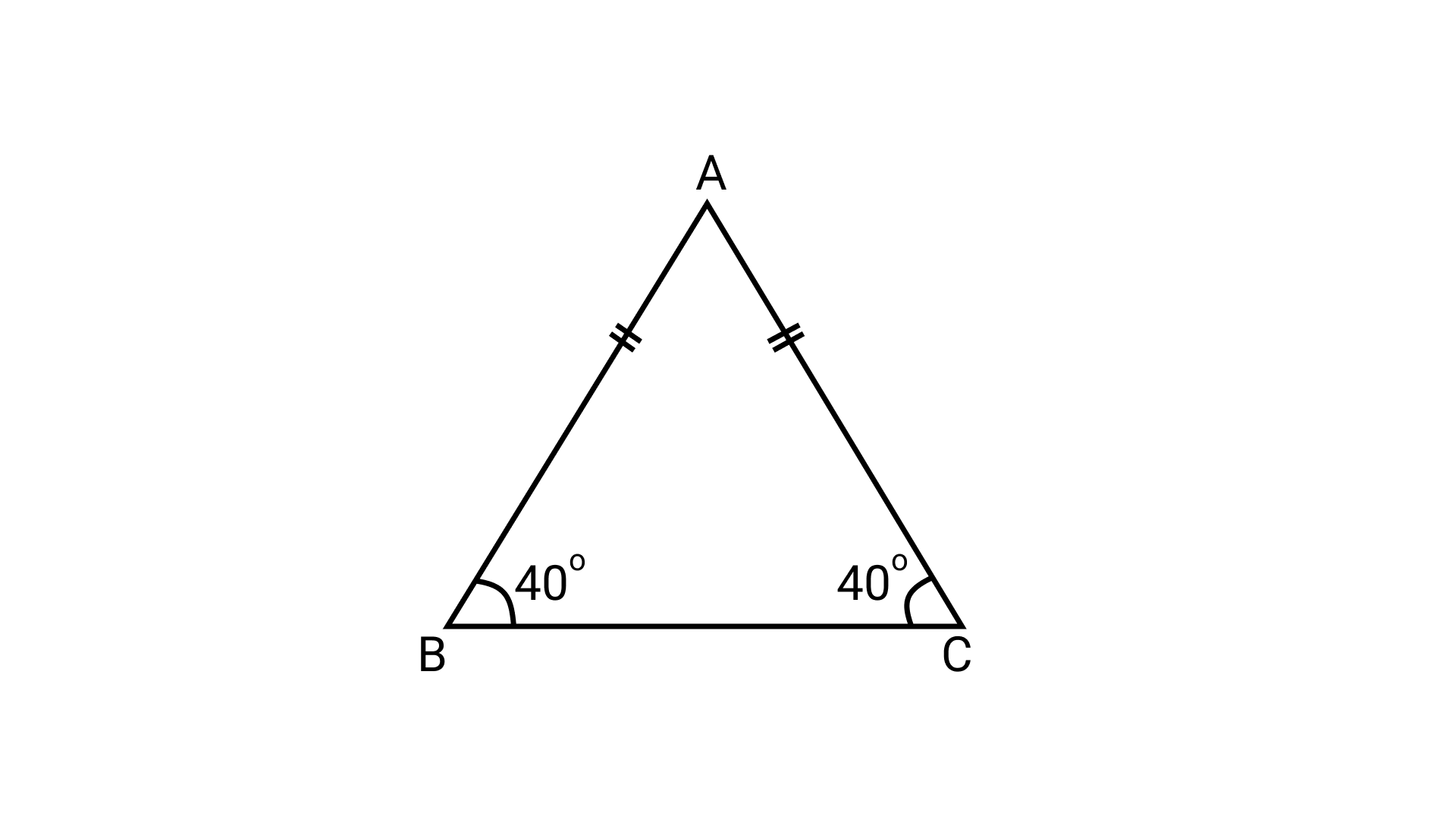
Now, 

\[\angle A{\text{ }} + \angle B{\text{ }} + \angle C{\text{ }} = {\text{ }}180^\circ \](Angle sum property)

\[\Rightarrow \angle A{\text{ }} = {\text{ }}180^\circ -40^\circ -40^\circ  = {\text{ }}100^\circ \] (Each base angle is $40^\circ$)

Thus, $\triangle \mathrm{ABC}$ is an obtuse angled triangle.

15. If two angles of a triangle are $60^\circ$ each, then the triangle is
(a) Isosceles but not equilateral

(b) Scalene

(c) Equilateral

(d) Right – angled.

Ans: Option (c) is correct.

Let $\triangle \mathrm{ABC}$ be the given triangle in which two angles are of $60^\circ$ each.

Now, 

\[\angle A{\text{ }} + \angle B{\text{ }} + \angle C{\text{ }} = {\text{ }}180^\circ \](Angle sum property)

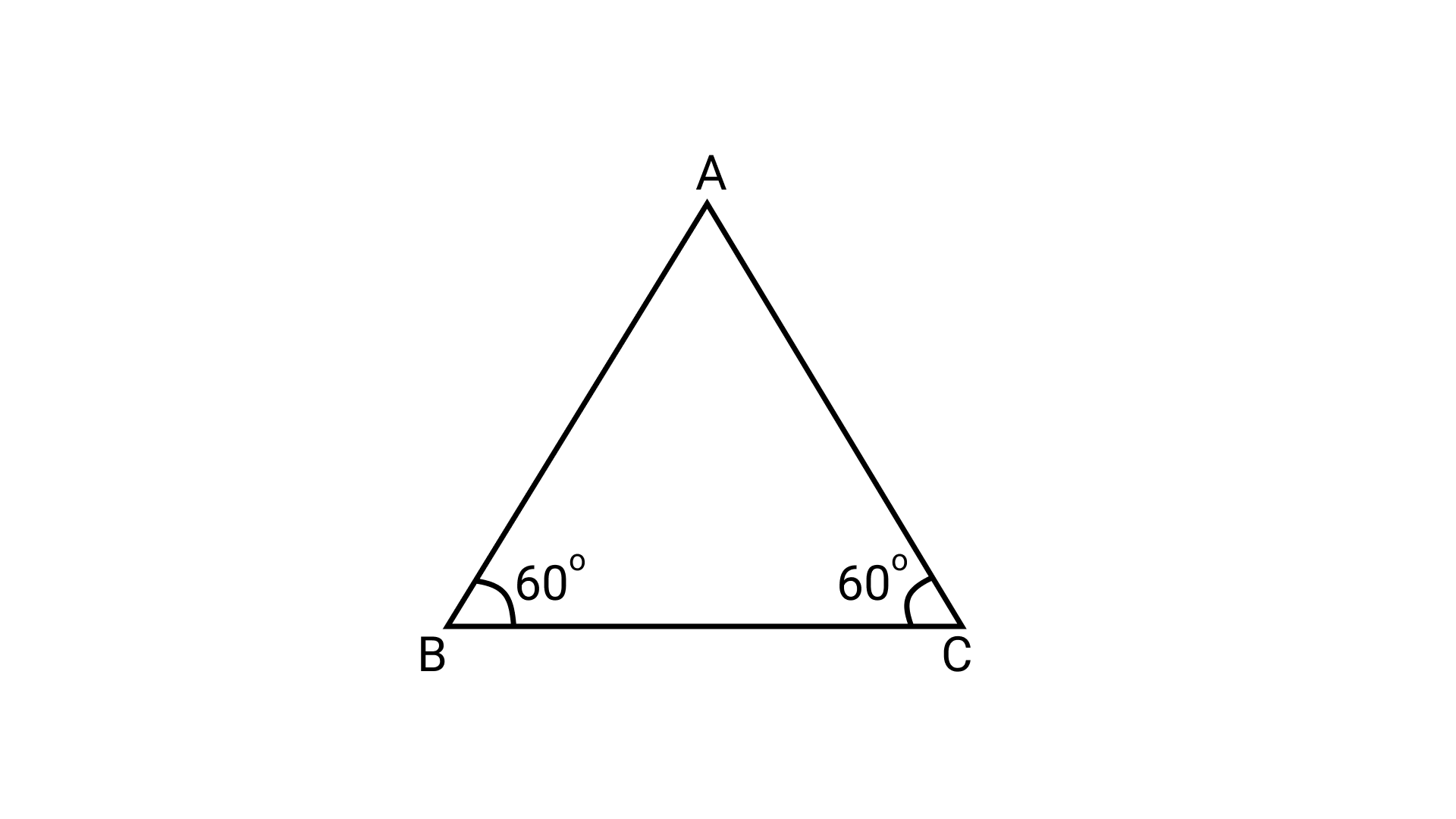
$\Rightarrow \angle A{\text{ }} = {\text{ }}180^\circ -60^\circ -60^\circ$

$\therefore \angle A{\text{ }} = {\text{ }}60^\circ$
Thus, all angles are of \[60^\circ \].

Therefore, $\triangle \mathrm{ABC}$ is an \[60^\circ \] equilateral triangle

16. The perimeter of the rectangle whose length is 60 cm and a diagonal is 61 cm is

(a) 120 cm

(b) 122 cm

(c) 71 cm

(d) 142 cm

Ans: Option (d) is correct.

Let $\triangle$BCD be the given rectangle such that AB =CD = 60 cm and AC = 61 cm.

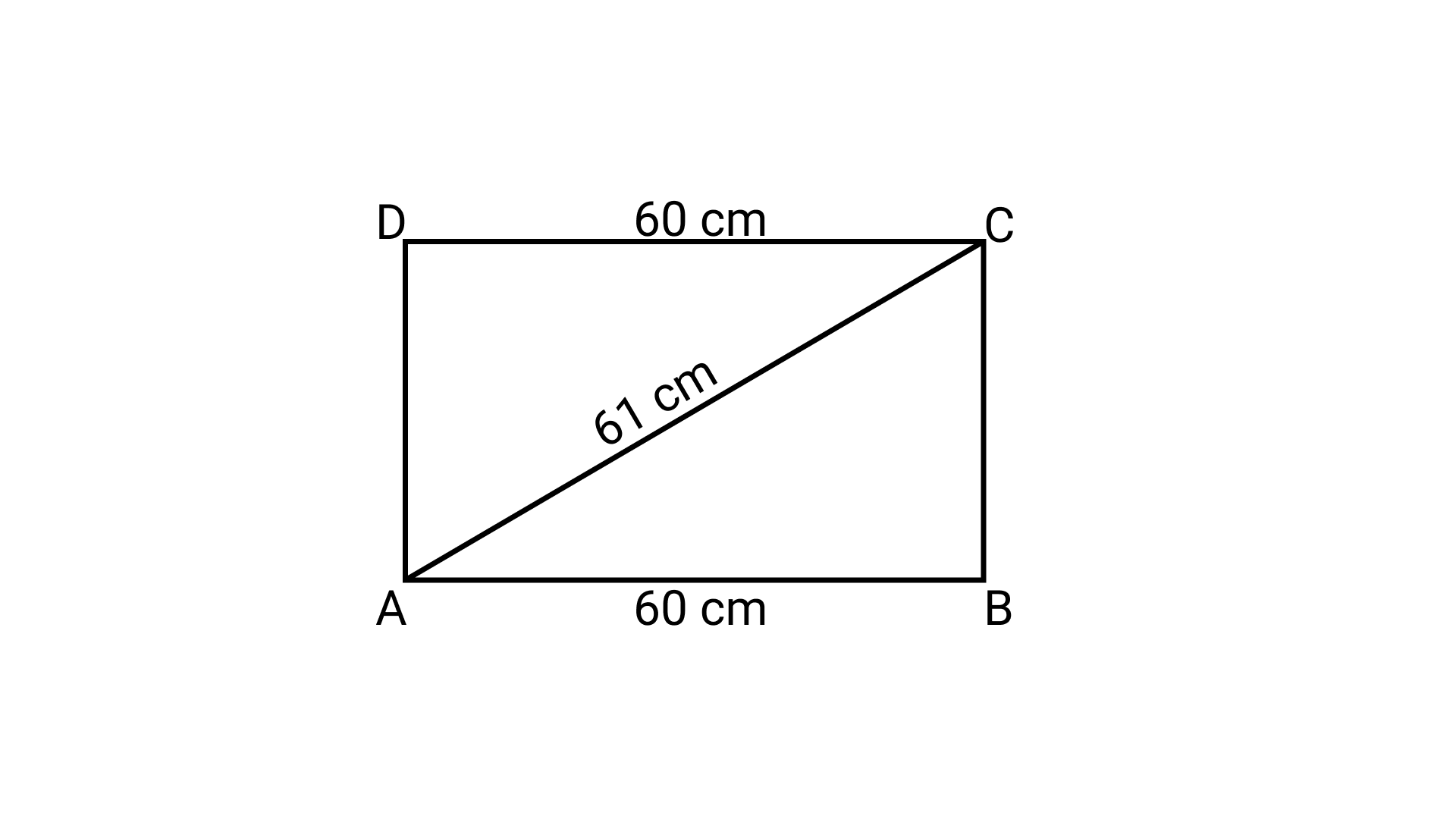
In $\triangle \mathrm{ABC}$,

${\left( {AC} \right)^2}\; = {\text{ }}{\left( {AB} \right)^2}\; + {\text{ }}{\left( {BC} \right)^2}$

$\Rightarrow {\left( {61} \right)^2}\; = {\text{ }}{\left( {60} \right)^2}\; + {\text{ }}{\left( {BC} \right)^2}$

$\Rightarrow {\left( {BC} \right)^2}\; = {\text{ }}3721{\text{ }}-{\text{ }}3600{\text{ }} = {\text{ }}121{\text{ }} = {\text{ }}{11^2}$

$\Rightarrow BC{\text{ }} = {\text{ }}11{\text{ cm}}$
Hence, 

${\text{Perimeter of rectangle }}ABCD{\text{ }} = {\text{ }}2\left( {AB{\text{ }} + {\text{ }}BC} \right)$ 

$= {\text{ }}2{\text{ }}\left( {60{\text{ }} + {\text{ }}11} \right){\text{ }}$ 

$= {\text{ }}2\left( {71} \right){\text{ }}$ 

$= {\text{ }}142{\text{ cm}}$ 

17. In $\triangle$PQR, If PQ = OR and  $\angle$ Q=$100^\circ$, then  $\angle$ R is equal to

(a) $40^\circ$

(b) $80^\circ$

(c) $120^\circ$

(d) $50^\circ$

Ans: Option (a) is correct.

${\text{Let}}\angle R{\text{ }} = {\text{ }}x$

$  PQ{\text{ }} = {\text{ }}QR{\text{ }}\left( {{\text{given}}} \right)$

$\therefore \angle R{\text{ }} = \angle P{\text{ }} = {\text{ }}x$ 

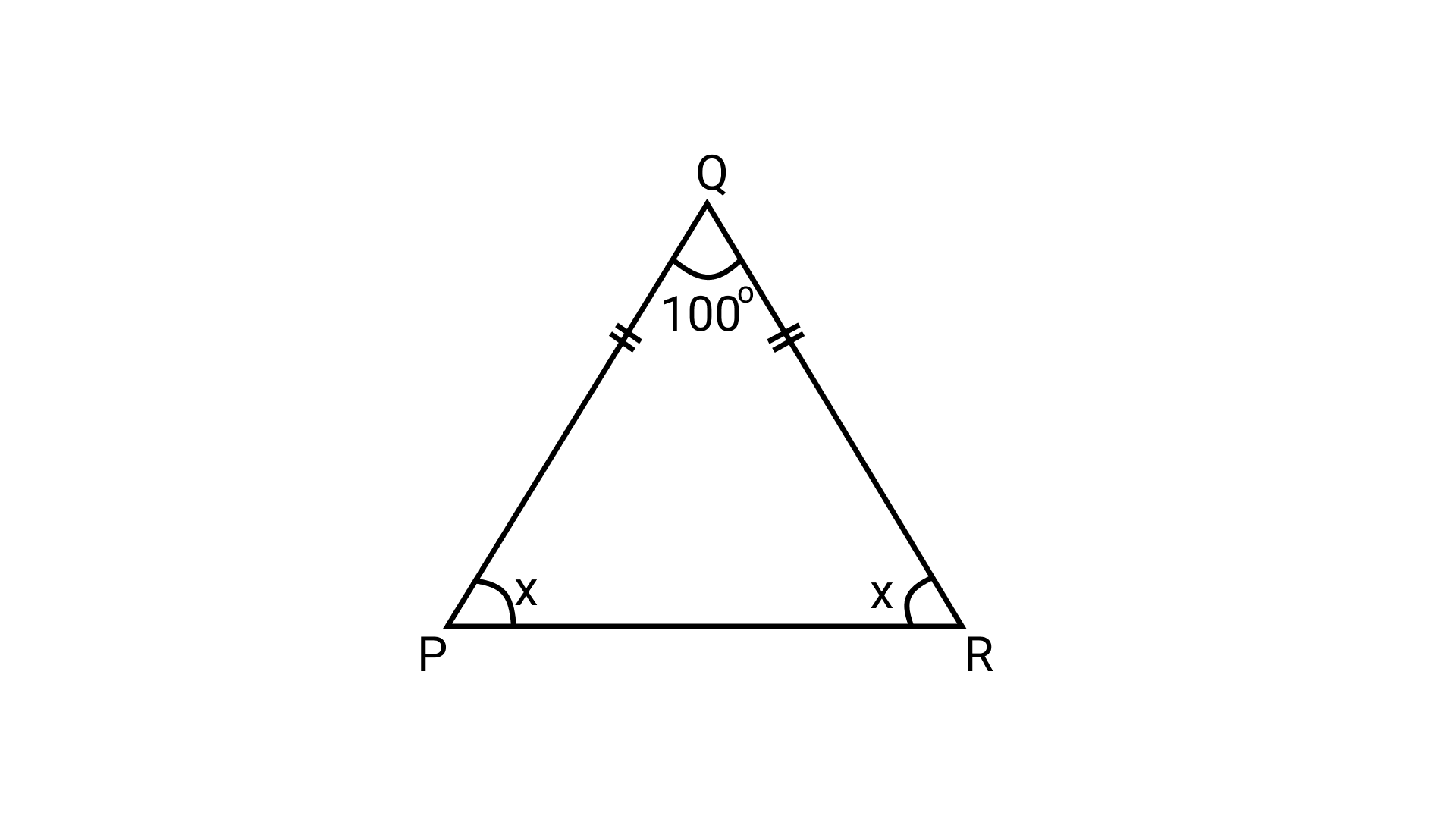
Now, in $\triangle$PQR

\[\angle P{\text{ }} + \angle Q{\text{ }} + \angle R{\text{ }} = {\text{ }}180^\circ \] (Angle sum property)

$\Rightarrow x{\text{ }} + {\text{ }}100^\circ  + {\text{ }}x{\text{ }} = {\text{ }}180^\circ$ 

$\Rightarrow 2x{\text{ }} = {\text{ }}180^\circ -100^\circ  = {\text{ }}80^\circ$ 

$\Rightarrow x = \frac{{80^\circ }}{2} = 40^\circ$
Thus, \[\angle R{\text{ }} = {\text{ }}40^\circ \].

18. Which of the following statements is not correct?

(a) The sum of any two sides of a triangle is greater than the third side

(b) A triangle can have all its angles acute

(c) A right-angled triangle cannot be equilateral

(d) Difference between any two sides of a triangle is greater than the third side

Ans: Option (d) is correct.

Since the difference of any two sides of a triangle is less than the third side.

19. In the given figure, BC = CA and  $\angle$ A = $40^\circ$. Then,  $\angle$ ACD is equal to the
(a) $40^\circ$

(b) $80^\circ$

(c) $120^\circ$

(d) $60^\circ$

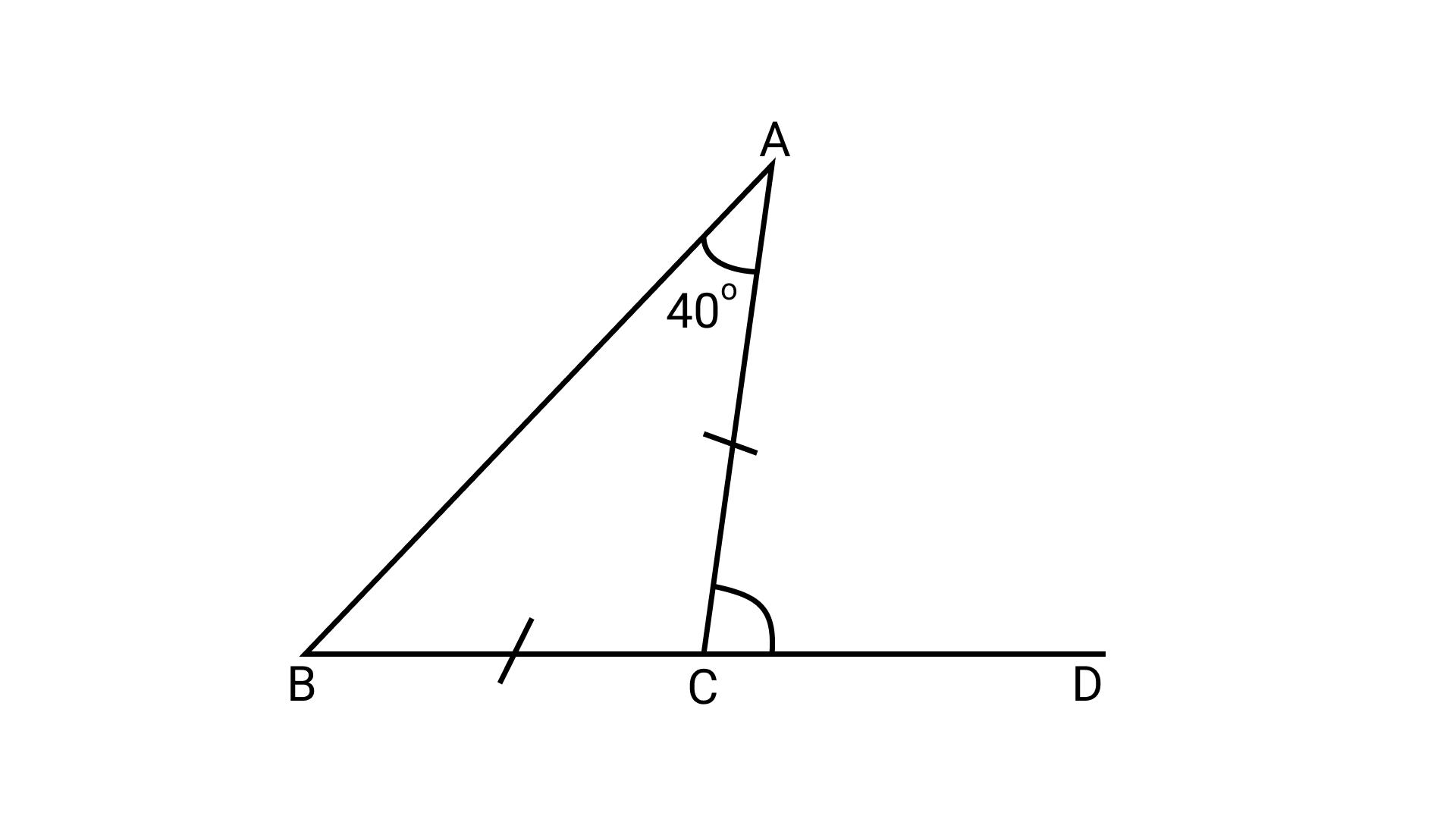
Ans: Option (b) is correct.

BC = CA (given)

\[\Rightarrow \angle A{\text{ }} = \angle B{\text{ }} = {\text{ }}40^\circ \] (\[\because \]Angles opposite to equal sides are equal)
Now, 

\[\angle ACD{\text{ }} = \angle A{\text{ }} + \angle B\](Exterior angle property)

$\angle ACD = {\text{ }}40^\circ  + {\text{ }}40^\circ$ 

$= {\text{ }}80^\circ$ 

20. The length of two sides of a triangle are 7 cm and 9 cm. The length of the third side may lie between

(a) 1 cm and 10 cm

(b) 2 cm and 8 cm

(c) 2 cm and 16 cm

(d) 1 cm and 16 cm

Ans: Option (c) is correct.

Length of two sides of a triangle are 7 cm and 9 cm.

Let the length of the third side be x cm.

Since, the sum of two sides is greater than the third side in a triangle.

$\therefore 7{\text{ }} + {\text{ }}9{\text{ }} > {\text{ }}x{\text{ or }}7{\text{ }} + {\text{ }}x{\text{ }} > {\text{ }}9{\text{ or }}9{\text{ }} + {\text{ }}x{\text{ }} > {\text{ }}7$

$\Rightarrow 16{\text{ }} > {\text{ }}x{\text{ or }}x{\text{ }} > {\text{ }}2{\text{ or }}x{\text{ }} > {\text{ }} - 2$ 

Since, side length cannot be negative.

\[\therefore 2{\text{ }} < {\text{ }}x{\text{ }} < {\text{ }}16\]
Thus, the third side may lie between 2 cm and 16 cm.

21. From the given figure, the value of x is
(a) $75^\circ$

(b) $90^\circ$

(c) $120^\circ$

(d) $60^\circ$

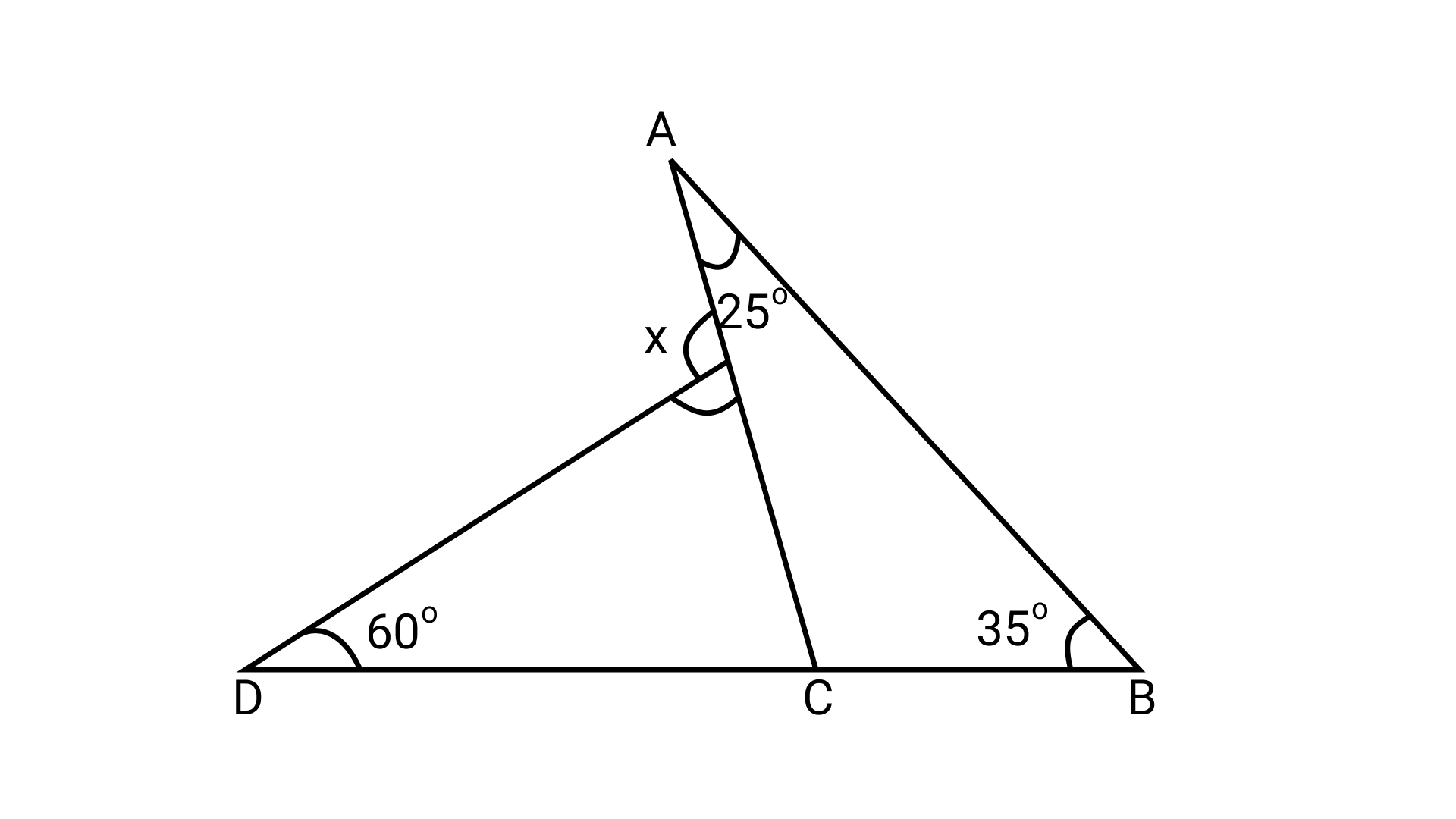
Ans: Option (c) is correct.

In $\triangle$ABC, 

By exterior angle property,

$\angle$ ACD = $\angle$ CAB +  $\angle$ ABC

$\Rightarrow$  $\angle$ ACD = $25^\circ$ + $35^\circ$

$\Rightarrow$  $\angle$ ACD = $60^\circ$ ………. (i)

Again, use exterior angle property,

x =  $\angle$ D + $\angle$ ACD 

$\Rightarrow$ x = $60^\circ$ + $60^\circ$ (Using equation (i)) 

Therefore, x = $120^\circ$

22. In the given figure, the value of  $\angle$ A + $\angle$ B + $\angle$ C +  $\angle$ D +  $\angle$ E  + $\angle$ F is
(a) 1$90^\circ$

(b) 5$40^\circ$

(c) 3$60^\circ$

(d) $180^\circ$

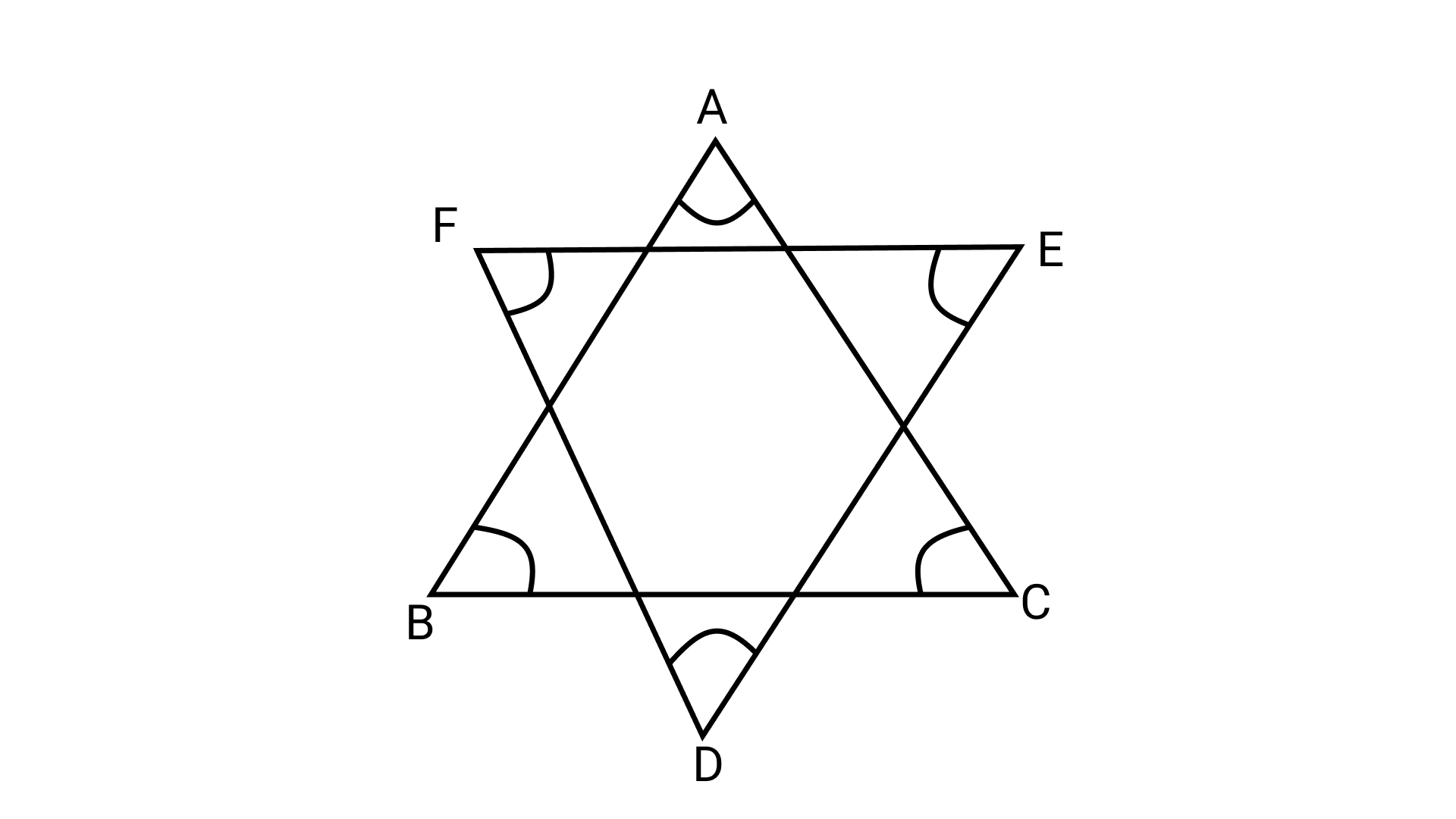
Ans: Option (c) is correct.

In $\triangle$ABC,

$\angle$ A +  $\angle$ B +  $\angle$ C = $180^\circ$ ………… (i) (By angle sum property)
In $\triangle$DEF,

$\angle$ D+  $\angle$ E +  $\angle$ F = $180^\circ$ ………..(ii) (By angle sum property)

Add equations (i) and (ii),

$\angle$ A +  $\angle$ B +  $\angle$ C +  $\angle$ D +  $\angle$ E +  $\angle$ F = $180^\circ$ + $180^\circ$ = 3$60^\circ$

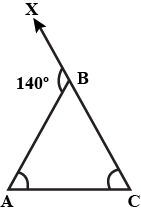
23. In the given figure, PQ = PR, RS = RQ, and ST||QR. If the exterior angle RPU is 1$40^\circ$, then the measure of angle TSR is 

(a) $55^\circ$

(b) $40^\circ$

(c) $50^\circ$

(d) $45^\circ$

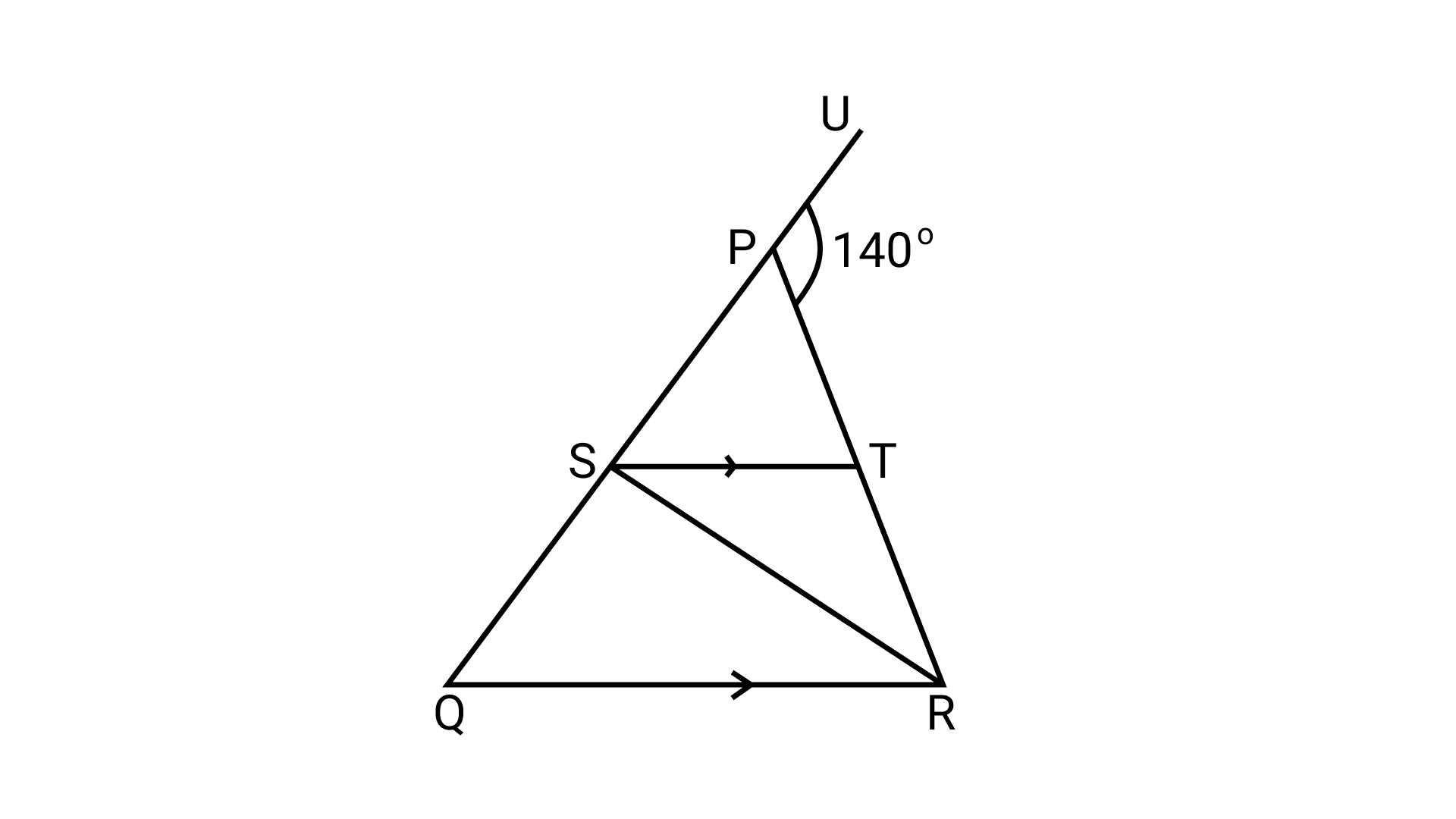
Ans: Option (b) is correct.

In $\triangle$PQR,

$\angle$ RPU =  $\angle$ PRQ +  $\angle$ PQR (Exterior angle property)

$\Rightarrow$ 1$40^\circ$ = 2  $\angle$ POR (Since PQ = PR, ∴  $\angle$ PRQ =  $\angle$ PQR)

\[\Rightarrow \angle PQR = \frac{{140^\circ }}{2} = 70^\circ \]
ST || QR and QS is a transversal.

∴  $\angle$ PST =  $\angle$ PQR = $70^\circ$ ………. (i) (Corresponding angles)

Now, in $\triangle$QSR 

RS = RQ (given) 

∴  $\angle$ SQR =  $\angle$ RSQ = $70^\circ$ ………. (ii) 

Now, PQ is a straight line.

So,  $\angle$ PST +  $\angle$ TSR +  $\angle$ RSQ = $180^\circ$

$\Rightarrow$ $70^\circ$ +  $\angle$ TSR + $70^\circ$ = $180^\circ$ (Using equations (i) and (ii))

$\Rightarrow$  $\angle$ TSR = $180^\circ$ – $70^\circ$ – 70 = $40^\circ$

24. In the given figure,  $\angle$ BAC = $90^\circ$, AD ⊥ BC and  $\angle$ BAD = $50^\circ$, then  $\angle$ ACD is
(a) $50^\circ$

(b) $40^\circ$

(c) $70^\circ$

(d) $60^\circ$

Ans: Option (d) is correct.

(a) Given that

$\angle$ BAC = $90^\circ$ and  $\angle$ BAD = $50^\circ$

∴  $\angle$ DAC =  $\angle$ BAC –  $\angle$ BAD = $90^\circ$ – $50^\circ$ = $40^\circ$

Now, in $\triangle$ADC,

$\angle$ ADB =  $\angle$ DAC +  $\angle$ ACD (Exterior angle property)

$\Rightarrow$ $90^\circ$ = $40^\circ$ +  $\angle$ ACD (∵ AD ⊥ BC)

$\Rightarrow$  $\angle$ ACD = $90^\circ$ – $40^\circ$ = $50^\circ$

25. If one angle of a triangle is equal to the sum of the other two angles, the triangle is

(a) obtuse

(b) acute

(c) right

(d) equilateral

Ans: Option (c) is correct.

Let angles of a triangle be x, y, z such that x = y + z ………. (i)

Now, 

x + y + z = $180^\circ$ (By angle sum property)

$\Rightarrow$ x + x = $180^\circ$ (Using equation (i))

$\Rightarrow 2x{\text{ }} = {\text{ }}180^\circ$

$\Rightarrow x = \frac{{180^\circ }}{2} = 90^\circ$ 

Thus, the triangle is right angled.

26. If the exterior angle of a triangle is 1$30^\circ$ and its interior opposite angles are equal, then measure of each interior opposite angle is

(a) $55^\circ$

(b) 65°

(c) $50^\circ$

(d) $60^\circ$

Ans: Option (b) is correct.

Let the interior opposite angles are x and x.

∴ 1$30^\circ$ = x + x (By exterior angle property)

$\Rightarrow$ 2x = 1$30^\circ$

$\Rightarrow x = \frac{{130^\circ }}{2}$

$\Rightarrow x = 65^\circ$ 

Thus, each interior opposite angle is of 65°

27. If one of the angles of a triangle is $110^\circ$, then the angle between the bisectors

of the other two angles is

(a) $70^\circ$

(b) $110^\circ$

(c) $35^\circ$

(d) 1$45^\circ$

Ans: Option (d) is correct.

Let $\triangle$ABC be the given triangle such that  $\angle$ A = $110^\circ$ and OB, OC are the angle

bisectors of  $\angle$ B,  $\angle$ C respectively.

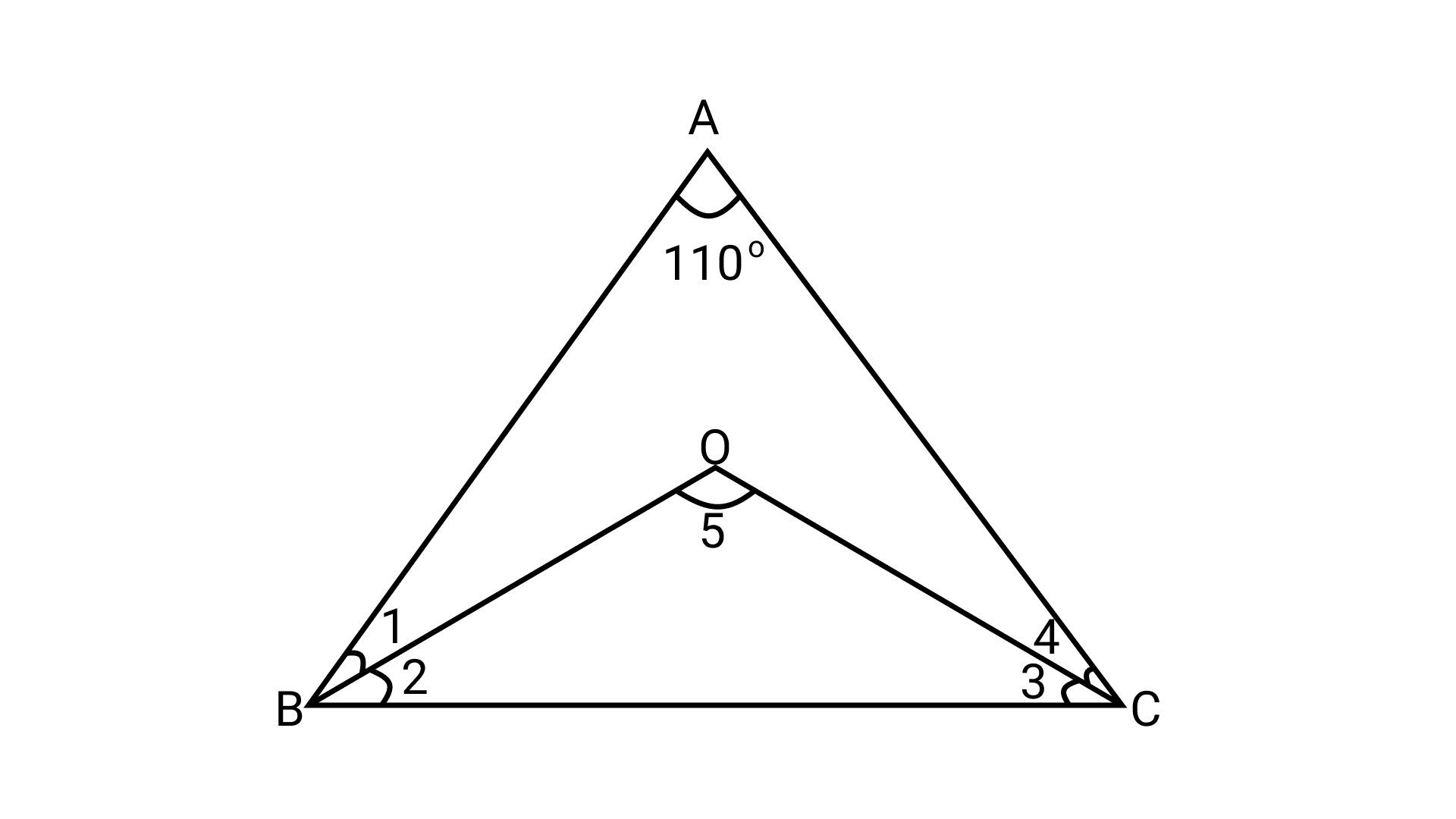
∴ $\angle$ 1 = $\angle$ 2,  $\angle$ 3 = 4 ………. (i)

In $\triangle$ΑΒC,

$\angle$ A +  $\angle$ B +  $\angle$ C = $180^\circ$ (By angle sum property)

$\Rightarrow$ $110^\circ$ + $\angle$ 1 +  $\angle$ 2 +  $\angle$ 3 +  $\angle$ 4 = $180^\circ$

$\Rightarrow$ 2( $\angle$ 2) +2( $\angle$ 3) = $180^\circ$ – $110^\circ$ (Using (1))

$\Rightarrow$ 2( $\angle$ 2 +  $\angle$ 3) = $70^\circ$

$\Rightarrow \angle 2 + \angle 3 = \frac{{70^\circ }}{2}$

$\Rightarrow \angle 2 + \angle 3 = 35^\circ \; \ldots  \ldots  \ldots  \ldots \left( {{\text{ii}}} \right)$ 

Now, in $\triangle$OBC

$\angle$ BOC +  $\angle$ OBC + $\angle$ OCB = $180^\circ$ (Angle sum property)

$\Rightarrow$  $\angle$ BOC +  $\angle$ 2 +  $\angle$ 3 = $180^\circ$

$\Rightarrow$  $\angle$ BOC = $180^\circ$ – $35^\circ$ = 1$45^\circ$ (Using equation (ii))

Hence, the required angle is 1$45^\circ$.

28. In $\triangle$ABC, AD is the bisector of  $\angle$ A meeting BC at D, CF ⊥ AB and E is the mid-point of AC. Then median of the triangle is

(a) AD

(b) BE

(c) FC

(d) DE

Ans: Option (b) is correct.

Since, the median of a triangle divides the opposite side into two equal parts. 

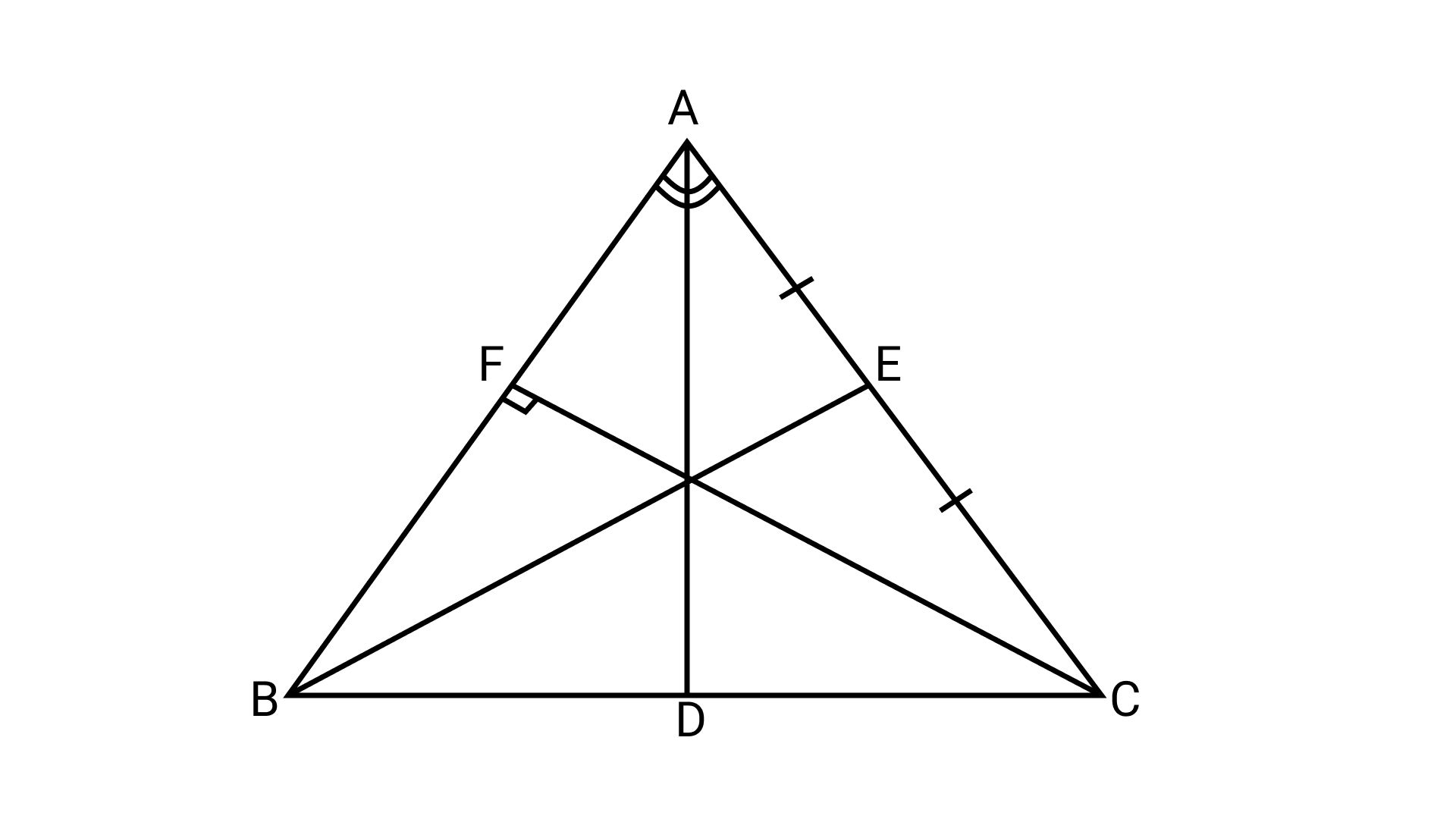
Therefore, BE is the median.

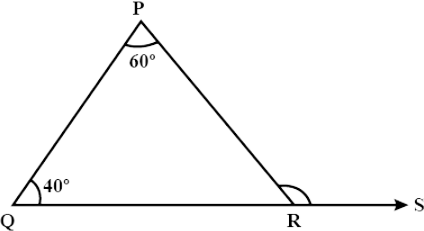
29. In $\triangle$PQR, if  $\angle$ P = $60^\circ$, and  $\angle$ Q = $40^\circ$, then the exterior angle formed by producing QR is equal to

(a) $60^\circ$

(b) $120^\circ$

(c) $100^\circ$

(d) $80^\circ$

Ans: Option (c) is correct.

Consider QR is produced to a point S.

In $\triangle$POR, 

$\angle$ PRS =  $\angle$ P +  $\angle$ Q (By exterior angle property)

$\angle$ PRS = $60^\circ$ + 40 = $100^\circ$

30. Which of the following triplets cannot be the angles of a triangle?

(a) 67°, 51°, 62°

(b) $70^\circ$, 83°, 27°

(c) $90^\circ$, $70^\circ$, $20^\circ$

(d) $40^\circ$, 132°, 18°

Ans: Option (d) is correct.

It is known that the sum of angles of a triangle is $180^\circ$ but $40^\circ$ + 132° + 18° = 1$90^\circ$

Therefore, $40^\circ$, 132°, 18° cannot be the angles of a triangle.

31. Which of the following can be the length of the third side of a triangle whose two sides measure 18 cm and 14 cm?

(a) 4 cm

(b) 3 cm

(c) 5 cm

(d) 32 cm

Ans: Option (c) is correct.

Let the third side of the triangle be x cm.

Since, the sum of any two sides of a triangle is greater than the third side.

∴ 18 + x > 14 or 14 + x > 18 or 18 + 14 > x

$\Rightarrow$ x > -4 or x > 4 or 32 > x

Since length cannot be negative, thus 4 < x < 32.

Hence, the third side of the triangle can be 5 cm from the available options.

32. How many altitudes does a triangle have?

(a) 1

(b) 3

(c) 6

(d) 9

Ans: Option (b) is correct.

A triangle has three altitudes.

33. If we join a vertex to a point on the opposite side which divides that side in the ratio 1:1, then what is the special name of that line segment?

(a) Median

(b) Angle bisector

(c) Altitude

(d) Hypotenuse

Ans: Option (a) is correct.

Median is a line segment which divides the opposite side into the ratio of 1 : 1.

34. The measures of x and y in the given figure are respectively
(a) $30^\circ$, $60^\circ$

(b) $40^\circ$, $40^\circ$

(c) $70^\circ$, $70^\circ$

(d) $70^\circ$, $60^\circ$

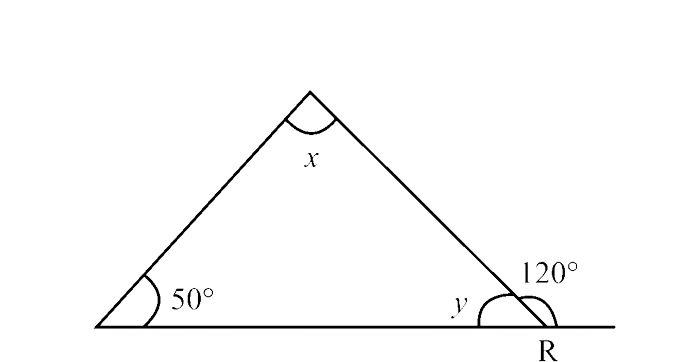
Ans: Option (d) is correct.

In $\triangle$PQR, 

$\angle$ PRS =  $\angle$ RPQ +  $\angle$ POR (By exterior angle property)

$\Rightarrow$ $120^\circ$ = x + $50^\circ$

$\Rightarrow$ x = $120^\circ$- $50^\circ$ = $70^\circ$

Now, 

x + y + $50^\circ$ = $180^\circ$ (By angle sum property)

$\Rightarrow$ $70^\circ$ + y + $50^\circ$ = $180^\circ$

$\Rightarrow$ y = $180^\circ$ – $70^\circ$ – $50^\circ$ = $60^\circ$

Thus, x = $70^\circ$, y = $60^\circ$

35. If length of two sides of a triangle are 6 cm and 10 cm, then the length of the

third side can be

(a) 3 cm

(b) 4 cm

(c) 2 cm

(d) 6 cm

Ans: Option (d) is correct.

(d) Let the third side of the triangle be x cm.

Since, the sum of any two sides of a triangle is greater than the third side.

∴ 6 + x > 10 or 10 + x > 6 or 10 + 6 > x

$\Rightarrow$ x > 4 or x > -4 or x < 16

Since the length cannot be negative, thus 4 < x < 16.

Hence, the third side can be 6 cm from the available options.

36. In a right-angled triangle ABC, if angle B = $90^\circ$, BC = 3 cm and AC = 5 cm, then the length of side AB is

(a) 3 c

(b) 4 cm

(c) 5 cm

(d) 6 cm

Ans: Option (b) is correct.

In the right angled triangle $\triangle$ABC,

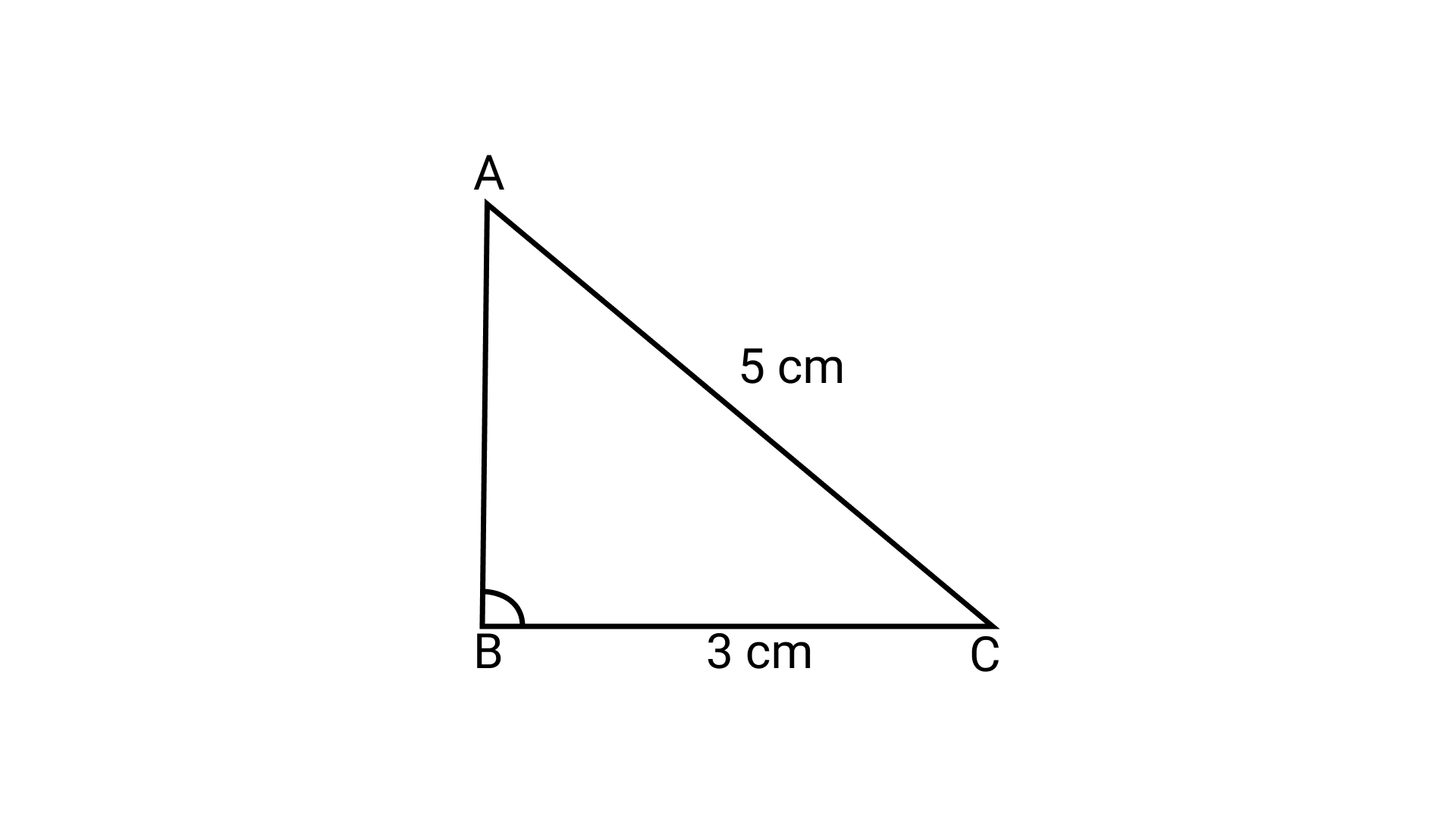
${\left( {AC} \right)^2}\; = {\text{ }}{\left( {AB} \right)^2}\; + {\text{ }}{\left( {BC} \right)^2}$

$\Rightarrow {5^2}\; = {\text{ }}{\left( {AB} \right)^2}\; + {\text{ }}{3^2}$

$\Rightarrow {\left( {AB} \right)^2}\; = {\text{ }}25{\text{ }}-{\text{ }}9{\text{ }} = {\text{ }}16{\text{ }} = {\text{ }}{4^2}$

$\Rightarrow AB{\text{ }} = {\text{ }}4{\text{ cm}}$ 

37. In a right-angled triangle ABC, if angle B = $90^\circ$, then which of the following is true?

(a) AB2 = BC2 + AC2

(b) AC2 = AB2 + BC2

(c) AB =BC + AC

(d) AC = AB + BC

Ans: Option (b) is correct.

In the right angled triangle ABC,

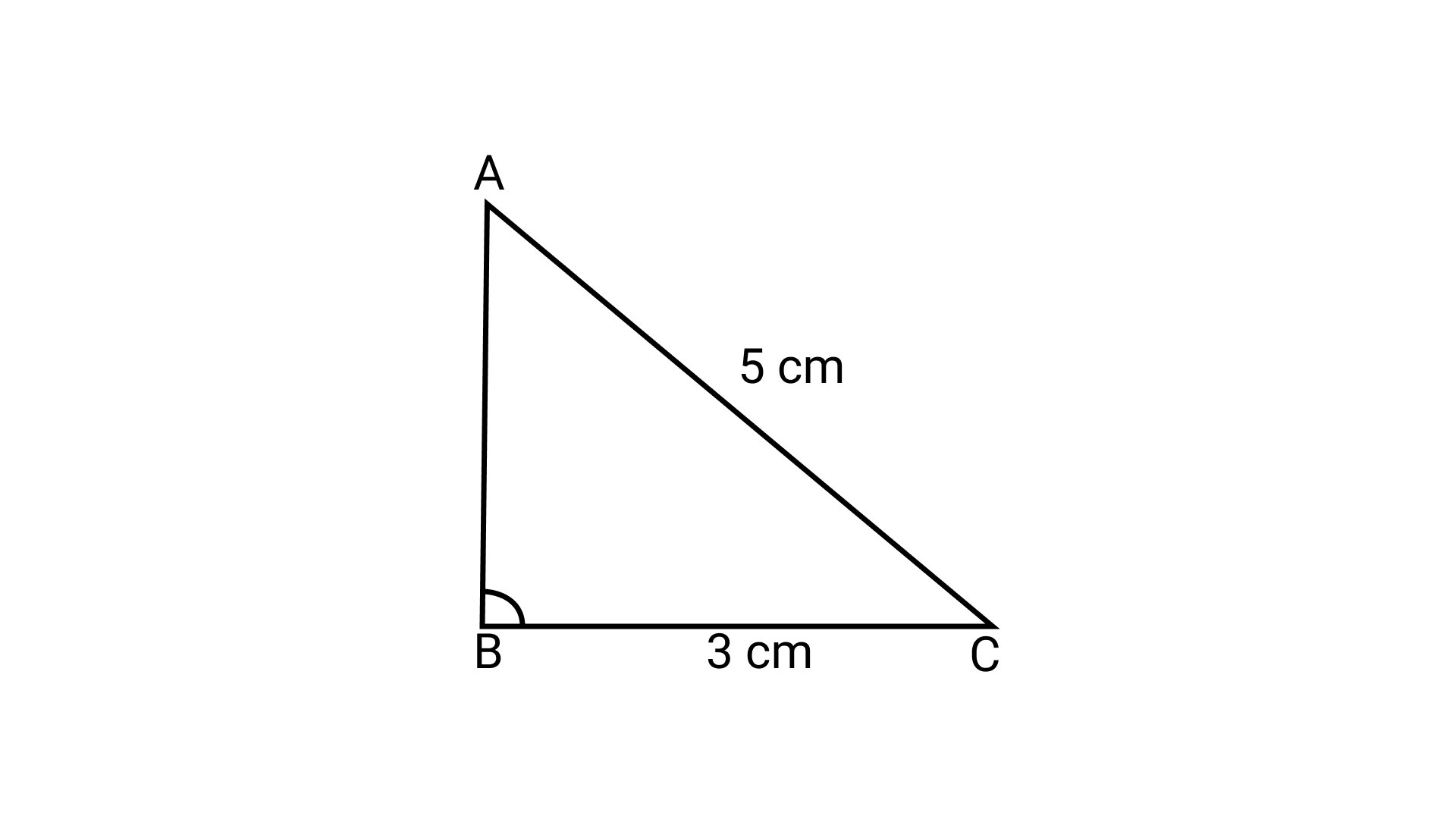
$\angle B = 90^\circ$ (Given)

Thus by Pythagoras theorem, 

(AC)2 = (AB)2 + (BC)2

38. Which of the following figures will have its altitude outside the triangle?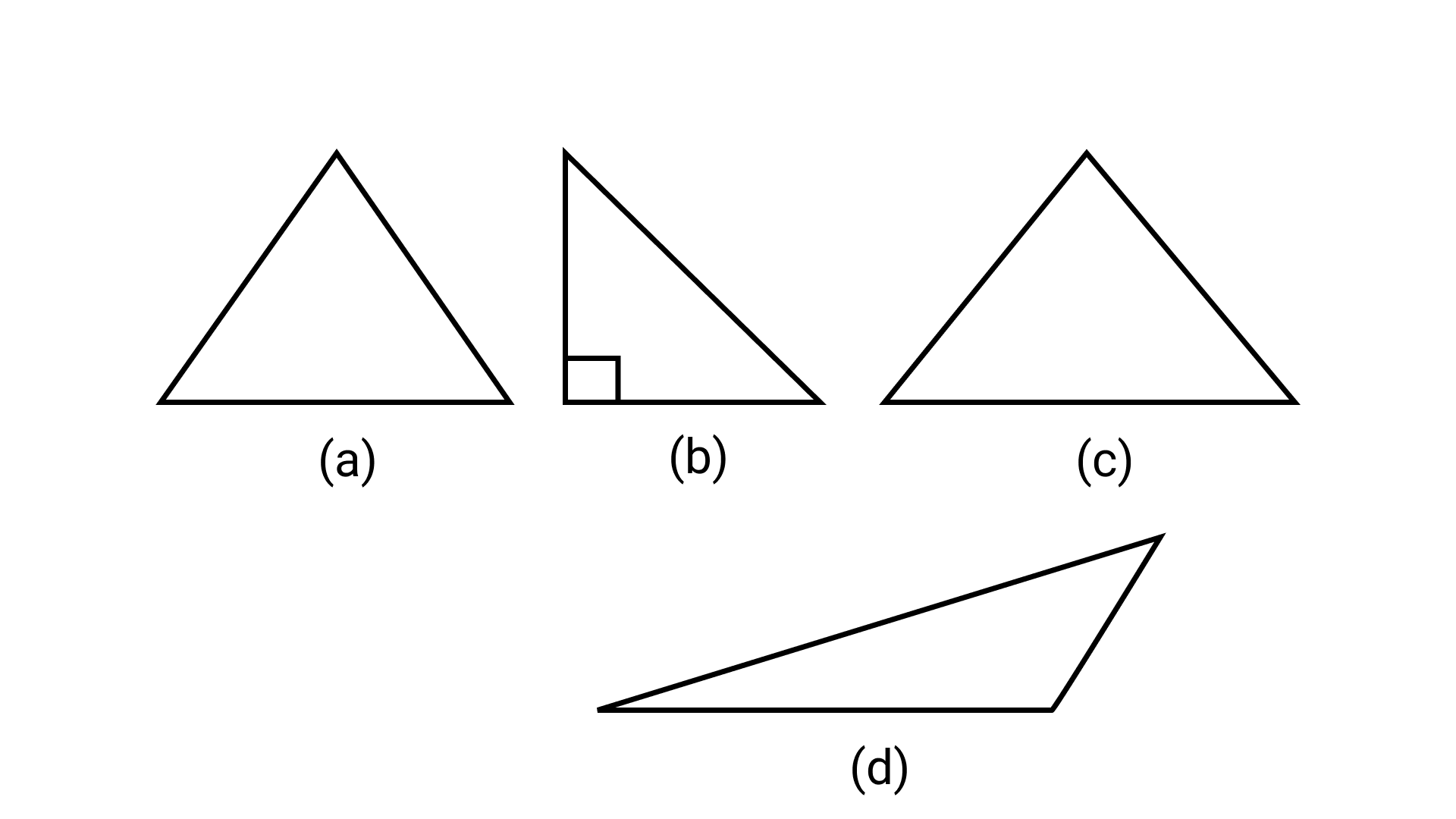

Ans: Option (d) is correct.

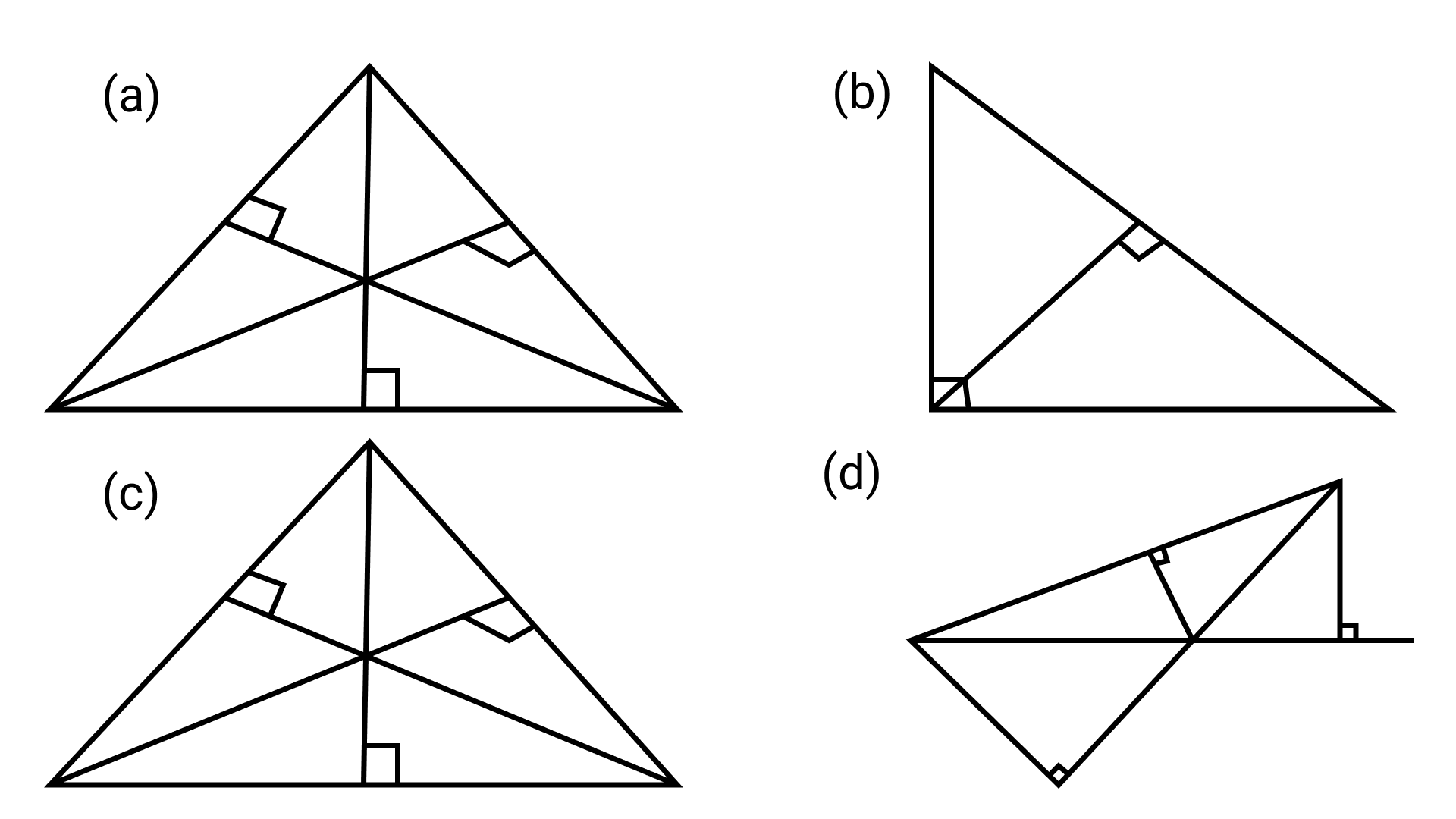
By drawing the altitudes it can be concluded that the triangle in option (d) has its altitude outside the triangle.

39. In the given figure, if AB|| CD, then
(a)  $\angle$ 2 =  $\angle$ 3

(b)  $\angle$ 1 =  $\angle$ 4

(c)  $\angle$ 4 =  $\angle$ 1 +  $\angle$ 2

(d)  $\angle$ 1 +  $\angle$ 2 =  $\angle$ 3 +  $\angle$ 4

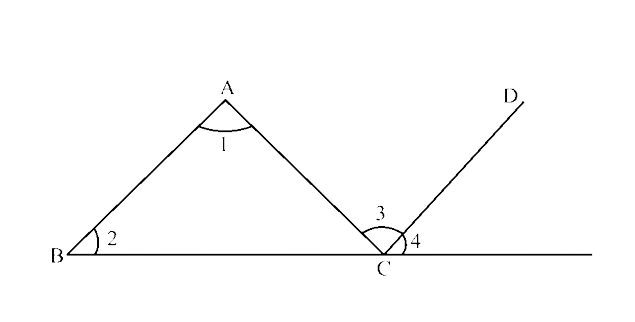
Ans: Option (d) is correct.

Given, AB || CD

∴  $\angle$ 2 =  $\angle$ 4 ……. (i) (Corresponding angles)

And  $\angle$ 1 =  $\angle$ 3 ………. (ii) (Alternate interior angles)

Add equations (i) and (ii), 

$\angle$ 1 +  $\angle$ 2 =  $\angle$ 3 +  $\angle$ 4

40. In $\triangle$ABC,  $\angle$ A = $100^\circ$, AD bisects  $\angle$ A and AD ⊥ BC. Then,  $\angle$ B is equal to
(a) $80^\circ$

(b) $20^\circ$

(c) $40^\circ$

(d) $30^\circ$

Ans: Option (c) is correct.

AD bisects,  $\angle$ A.

$\therefore \;\angle BAD = \angle DAC = \frac{1}{2}\angle BAC$

$\Rightarrow \angle BAD = \frac{{100^\circ }}{2} = 50^\circ$ 

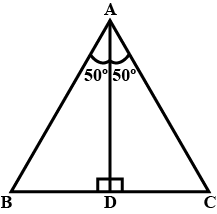
Now, AD ⊥ BC

∴  $\angle$ ADC = $90^\circ$

Now, in $\triangle$ABD,

$\angle$ ADC =  $\angle$ ABD +  $\angle$ BAD (By exterior angle property)

$\Rightarrow$ $90^\circ$ =  $\angle$ ABD + $50^\circ$

$\Rightarrow$  $\angle$ ABD = $90^\circ$- $50^\circ$ = $40^\circ$

Thus,  $\angle$ B = $40^\circ$

41. In $\triangle$ABC,  $\angle$ A = $50^\circ$,  $\angle$ B = $70^\circ$ and the bisector of  $\angle$ C meets AB in D (see figure).

Measure of  $\angle$ ADC is

(a) $50^\circ$

(b) $100^\circ$

(c) $30^\circ$

(d) $70^\circ$

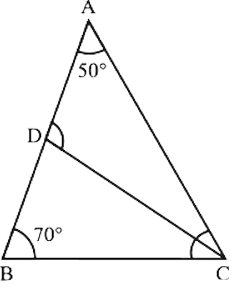
Ans: Option (b) is correct.

In $\triangle$ABC,  $\angle$ A + $\angle$ B +  $\angle$ C = $180^\circ$ (By angle sum property)

$\Rightarrow$  $\angle$ C = $180^\circ$ – $70^\circ$ – $50^\circ$

$\Rightarrow$  $\angle$ C = 60 °

Since, CD bisects  $\angle$ C.

$\therefore \;\angle DCB = \angle ACD = \frac{1}{2}\angle C$

$\Rightarrow \frac{1}{2}\angle C = \frac{{60^\circ }}{2} = 30^\circ$ 

Now, in $\triangle$BDC, 

$\angle$ ADC =  $\angle$ DBC +  $\angle$ DCB (By exterior angle property)

$\Rightarrow$  $\angle$ ADC = $70^\circ$ + 30 

$\Rightarrow$  $\angle$ ADC = $100^\circ$

42. If for $\triangle$ABC and $\triangle$DEF, the correspondence CAB ⟷ EDF gives a

congruence, then which of the following is not true?

(a) AC = DE

(b) AB = EF

(c)  $\angle$ A =  $\angle$ D

(d)  $\angle$ C =  $\angle$ E

Ans: Option (b) is correct.

Given that $\triangle$CAB ≅ $\triangle$EDF

∴ By C.P.C.T.

AC = DE, AB = DF, BC = FE

And 

$\angle$ A = $\angle$ D,  $\angle$ C =  $\angle$ E,  $\angle$ B =  $\angle$ F

43. In the given figure, M is the mid-point of both AC and BD. Then

(a)  $\angle$ 1 =  $\angle$ 2

(b)  $\angle$ 1 =  $\angle$ 4

(c)  $\angle$ 2 =  $\angle$ 4

(d)  $\angle$ 1 =  $\angle$ 3

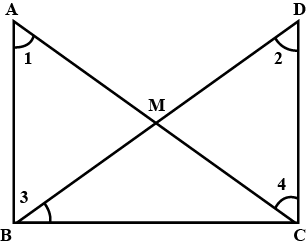
Ans: Option (b) is correct.

In $\triangle$AMB and $\triangle$CMD,

AM = CM (M is midpoint of AC)

BM = DM (M is midpoint of BD)

$\angle$ AMB =  $\angle$ CMD (Vertically opposite angles)

So, $\triangle$AMB ≅ $\triangle$CMD (By SAS criterion)And 

$\angle$ 1 =  $\angle$ 4 (By C.P.C.T)

44. If D is the midpoint of the side BC in $\triangle$ABC where AB = AC, then  $\angle$ ADC is

(a) $60^\circ$

(b) $45^\circ$

(c) $120^\circ$

(d) $90^\circ$

Ans: Option (d) is correct.

In $\triangle$ABD and $\triangle$ACD,

AD = AD (common)

AB = AC (given)

BD = CD (D is midpoint of BC)

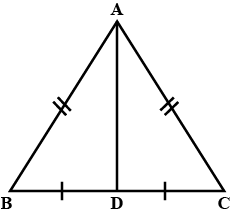
∴ $\triangle$ABD ≅ $\triangle$ACD (By SSS criterion)

∴  $\angle$ ADB =  $\angle$ ADC (By C.P.C.T)

But  $\angle$ ADB +  $\angle$ ADC = $180^\circ$ (As BC is a straight line)
$\Rightarrow$  $\angle$ ADC +  $\angle$ ADC = $180^\circ$

$\Rightarrow$ 2  $\angle$ ADC = $180^\circ$

$\Rightarrow$  $\angle$ ADC = $90^\circ$

45. Two triangles are congruent, if two angles and the side included between them in one of the triangles are equal to the two angles and the side included between them of the other triangle. This is known as the

(a) RHS congruence criterion

(b) ASA congruence criterion

(c) SAS congruence criterion

(d) AAA congruence criterion

Ans: Option (b) is correct.

It is known as ASA congruence criterion.

46. By which congruency criterion, the two triangles in the given figure are congruent?

(a) RHS

(b) ASA

(c) SSS

(d) SAS

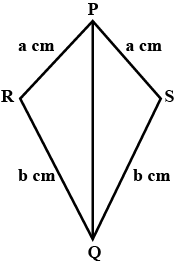
Ans: Option (c) is correct.

In $\triangle$PRQ and $\triangle$PSQ,

PQ = PQ (common side)

PR = PS = a cm (given)

QR = QS = b = cm (given)

So, $\triangle$PRQ ≅ $\triangle$PSQ (By SSS criterion)

47. By which of the following criterion two triangles cannot be proved congruent?

(a) AAA

(b) SSS

(c) SAS

(d) ASA

Ans: Option (a) is correct.

With AAA criterion two triangles cannot be proved congruent.

48. If $\triangle$PQR is congruent to $\triangle$STU (see figure), then what is the length of TU?

(a) 5 cm

(b) 6 cm

(c) 7 cm

(d) cannot be determined

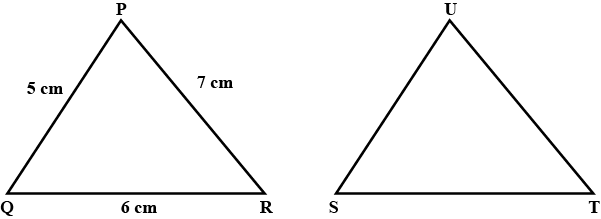
Ans: Option (b) is correct.

It is given that $\triangle$PQR ≅ $\triangle$STU.

∴ TU = QR = 6 cm (By C.P.C.T.)

49. If $\triangle$ABC and $\triangle$DBC are on the same base BC, AB = DC and AC = DB (see figure), then which of the following gives a congruence relationship?
(a) $\triangle$ABC ≅ $\triangle$DBC

(b) $\triangle$ABC ≅ $\triangle$CBD

(c) $\triangle$ABC ≅ $\triangle$DCB

(d) $\triangle$ABC ≅ $\triangle$BCD

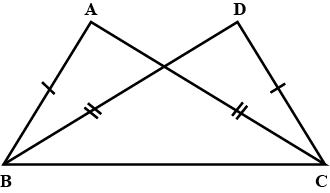
Ans: Option (c) is correct.

In $\triangle$ABC and $\triangle$DCB,

AB = DC (given)

AC = DB (given)

BC = CB (common)

∴ $\triangle$ABC ≅ $\triangle$DCB (By SSS criterion)

Directions: In questions 50 to 69, fill in the blanks to make the statements true.

50. The ________ triangle always has altitude outside itself.

Ans: Obtuse-angled

51. The sum of an exterior angle of a triangle and its adjacent angle is always ________

Ans: $180^\circ$

52. The longest side of a right-angled triangle is called its ________

Ans: Hypotenuse

53. Median is also called ________ in an equilateral triangle.

Ans: Altitude

54. Measures of each of the angles of an equilateral triangle is ________

Ans: $60^\circ$

55. In an isosceles triangle, two angles are always ________

Ans: Equal

56. In an isosceles triangle, angles opposite to equal sides are ________

Ans: Equal

57. If one angle of a triangle is equal to the sum of other two, then the measure

of that angle is ________

Ans: $90^\circ$

Consider the angles of the triangle be x, y and z.

Given that x = y + z ………… (i)

Now, x + y + z = $180^\circ$ (By angle sum property)

$\Rightarrow x{\text{ }} + {\text{ }}x{\text{ }} = {\text{ }}180^\circ \left( {{\text{Using }}\left( {\text{i}} \right)} \right)$

$\Rightarrow 2x{\text{ }} = {\text{ }}180^\circ$

$\Rightarrow x{\text{ }} = {\text{ }}\frac{{180^\circ }}{2}$

$\Rightarrow x{\text{ }} = {\text{ }}90^\circ$ 

58. Every triangle has at least ________ acute angle(s).

Ans: Two

59. Two-line segments are congruent, if they are ________ lengths.

Ans: Equal

60. Two angles are said to be ________ if they have equal measures.

Ans: Congruent

61. Two rectangles are congruent, if they have same ________ and ________

Ans: Length, breadth

62. Two squares are congruent, if they have same ________

Ans: Side

63. If $\triangle$PQR and $\triangle$XYZ are congruent under the correspondence QPR ⟷ XYZ,

Then

(i)  $\angle$ R = ________

Given that $\triangle$QPR ≅ $\triangle$XYZ

So, by C.P.C.T.

 $\angle$ R =  $\angle$ Z

(ii) QR = ________

QR = XZ

(iii)  $\angle$ P = ________

 $\angle$ P =  $\angle$ Y

(iv) QP = ________

QP = XY

(v)  $\angle$ Q = ________

 $\angle$ Q =  $\angle$ X

(vi) RP = ________

RP = ZY

64. In the given figure, $\triangle$PQR ≅ $\triangle$________

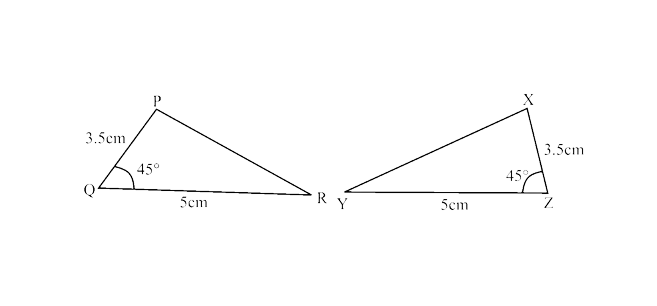
Ans: XZY 

In $\triangle$PQR and $\triangle$XZY,

PQ = XZ = 3.5 cm

 $\angle$ PQR =  $\angle$ XZY = $45^\circ$

QR = ZY = 5 cm

∴ $\triangle$PQR ≅ $\triangle$XZY (By SAS criterion)

65. In the given figure, $\triangle$PQR ≅ $\triangle$ ________

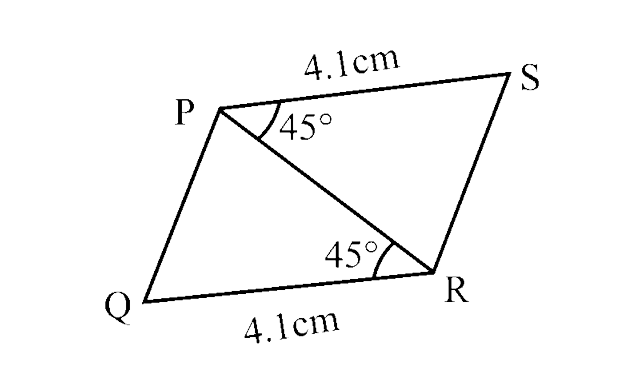
Ans: RSP 

In $\triangle$PQR and $\triangle$RSP,

QR = SP = 4.1 cm

$\angle$ PRQ =  $\angle$ RPS = $45^\circ$

PR = RP (common)

∴ $\triangle$PQR ≅ $\triangle$RSP (By SAS criterion)

66. In the given figure, $\triangle$ ________ ≅ $\triangle$PQR

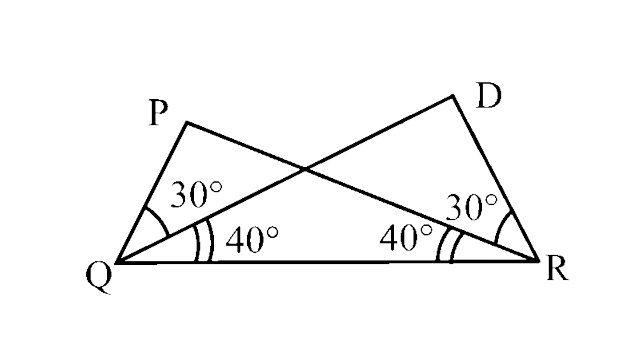
Ans: DRQ 

In $\triangle$PQR and $\triangle$DRQ,

$\angle$ PRQ =  $\angle$ DQR = $40^\circ$

$\angle$ PQR =  $\angle$ DRQ = $30^\circ$ + $40^\circ$ = $70^\circ$

QR = RQ (common)

∴ $\triangle$PQR ≅ $\triangle$DRQ (By ASA criterion)

67. In the given figure, $\triangle$ARO ≅ $\triangle$ __________

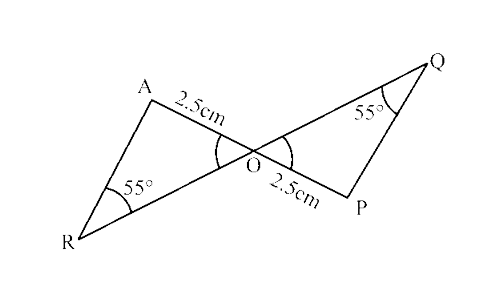
Ans: PQO 

In $\triangle$ARO and $\triangle$PQO,

$\angle$ ARO =  $\angle$ PQO = $55^\circ$

$\angle$ AOR =  $\angle$ POQ (Vertically opposite angles)

∴  $\angle$ RAQ =  $\angle$ QPO (∵ If two angles of a triangle are equal to two angles of another

triangle then third angle is also equal)

AO = PO = 2.5 cm

∴ $\triangle$ARO ≅ $\triangle$PQO (By ASA criterion)

68. In the given figure, AB = AD and  $\angle$ BAC =  $\angle$ DAC. 

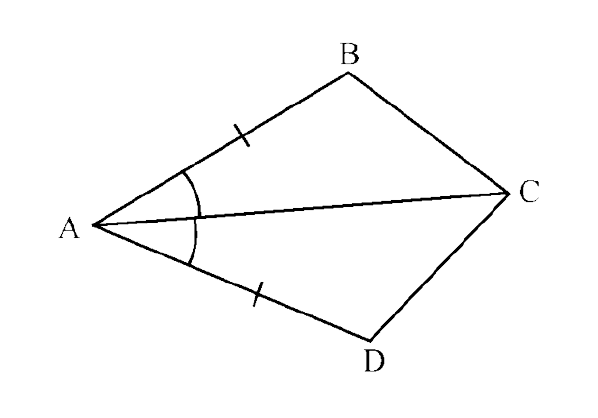
Then

(i) $\triangle$ ________ ≅ $\triangle$ABC.

Ans: ADC

In $\triangle$ABC and $\triangle$ADC,

AC = AC (common)

$\angle$ BAC =  $\angle$ DAC (given)

AB = AD (given)

∴ $\triangle$ABC ≅ $\triangle$ADC (By SAS criterion) 

(ii) BC = ________

Ans: DC

Since $\triangle$ABC ≅ $\triangle$ADC,

∴ BC = DC (By C.P.C.T.)

(iii)  $\angle$ BCA = ________

Ans:  $\angle$ DCA

Since $\triangle$ABC ≅ $\triangle$ADC,

∴  $\angle$ BCA =  $\angle$ DCA (By C.P.C.T.)

(iv) Line segment AC bisects ________ and ________

Ans:  $\angle$ BAD,  $\angle$ BCD

Since  $\angle$ BAC =  $\angle$ DAC (given),

∴ Line segment AC bisects  $\angle$ BAD and  $\angle$ BCD.

69. In the given figure,

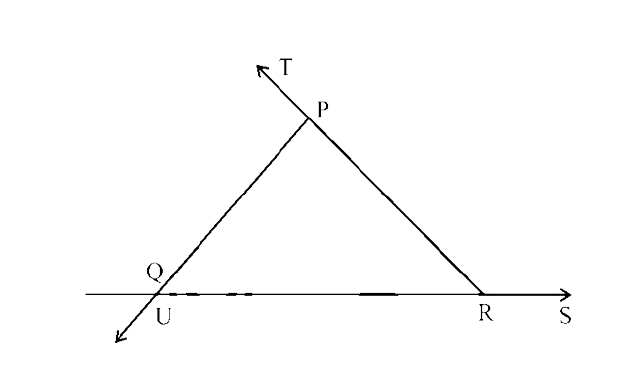
(i)  $\angle$ TPQ =  $\angle$  ______ +  $\angle$  _______

Ans: PQR, PRQ 

$\angle$ TPQ =  $\angle$ PQR +  $\angle$ PRQ (By exterior angle property)

(ii)  $\angle$ UQR =  $\angle$ ______ +  $\angle$  ______

Ans: QPR, QRP 

$\angle$ UQR =  $\angle$ QPR +  $\angle$ QRP (By exterior angle property)

(iii)  $\angle$ PRS =  $\angle$  ______ +  $\angle$  _______

Ans: RPQ, RQP 

$\angle$ PRS =  $\angle$ RPQ +  $\angle$ ROP (By exterior angle property) 

Directions: In questions 70 to 106 state whether the statements are True or

False.

70. In a triangle, sum of squares of two sides is equal to the square of the third

side.

Ans: False

Since, in a right-angled triangle, sum of squares of two sides is equal to the square

of the third side.

71. Sum of two sides of a triangle is greater than or equal to the third side.
Ans: False

Since, the sum of two sides of a triangle is greater than the third side.

72. The difference between the lengths of any two sides of a triangle is smaller than the length of the third side.

Ans: True

73. In $\triangle$ABC, AB = 3.5 cm, AC = 5 cm, BC = 6 cm and in $\triangle$POR, PR = 3.5 cm,

PQ = 5 cm, RQ = 6 cm. Then $\triangle$ABC ≅ $\triangle$PQR.

Ans: False

In $\triangle$ ABC and $\triangle$POR,

AB = PR = 3.5 cm

AC = PQ = 5 cm

BC = RO = 6 cm

∴ $\triangle$ ABC ≅ $\triangle$ PRQ (By SSS congruency)

74. Sum of any two angles of a triangle is always greater than the third angle.
Ans: False

Since, sum of any two angles of a triangle is may or may not be greater than the third

angle.

75. The sum of the measures of three angles of a triangle is greater than $180^\circ$

Ans: False

Since, the sum of the measures of three angles of a triangle is equal to $180^\circ$

76. It is possible to have a right-angled equilateral triangle.

Ans: False

Since, an equilateral triangle cannot be a right-angled triangle.

77. If M is the midpoint of a line segment AB, then we can say that AM and MB are congruent.

Ans: True

Since, M is midpoint of AB.

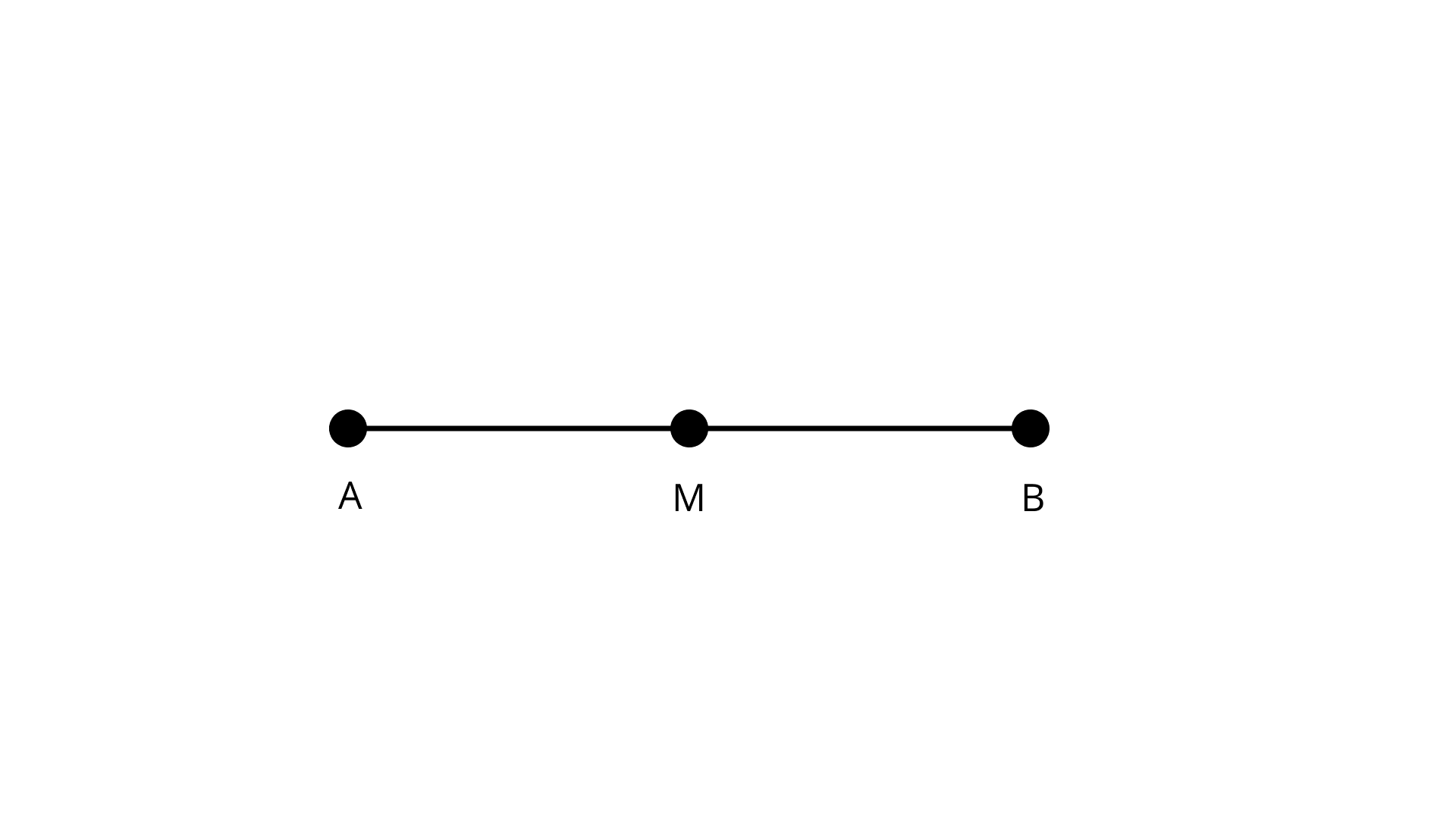
$\Rightarrow$ AM = MB

78. It is possible to have a triangle in which two of the angles are right angles.

Ans: False

Not more than one right- angle is possible in a triangle.

79. It is possible to have a triangle in which two of the angles are obtuse.

Ans: False

$\angle$ A +  $\angle$ B +  $\angle$ C = $180^\circ$ (By angle sum property)

If a triangle has two obtuse angles, then the sum of all the 3 interior angles will not be equal to $180^\circ$.

Thus, a triangle is not possible.

80. It is possible to have a triangle in which two angles are acute.

Ans: True

81. It is possible to have a triangle in which each angle is less than $60^\circ$

Ans: False

If all angles of a triangle are less than $60^\circ$, then their sum will be less than $180^\circ$. But

in a triangle sum of all angles is $180^\circ$.

∴ Triangle is not possible.

82. It is possible to have a triangle in which each angle is greater than $60^\circ$

Ans: False

If all angles of a triangle are greater than $60^\circ$, then their sum will be greater than

$180^\circ$. But in a triangle sum of all angles is $180^\circ$.

Since the sum of the angles of a triangle is always $180^\circ$, such a triangle is not possible.

83. It is possible to have a triangle in which each angle is equal to $60^\circ$

Ans: True

Since in an equilateral triangle each angle is equal to $60^\circ$.

84. A right-angled triangle may have all sides equal.

Ans: False

A right-angled triangle may have two sides equal.

85. If two angles of a triangle are equal, the third angle is also equal to each of

the other two angles.

Ans: False

If two angles of a triangle are equal then third angle may or may not be equal to each

of the other two angles.

86. In the given figure, two triangles are congruent by RHS.

Ans: False

Since, given triangles are congruent by SAS.

87. The congruent figures superimpose each other completely.

Ans: True

88. A one-rupee coin is congruent to a five-rupee coin.

Ans: False

Since one-rupee coin and five-rupee coin are of different size, they are not congruent.

89. The top and bottom faces of a kaleidoscope are congruent.

Ans: True

90. Two acute angles are congruent.

Ans: False

Since, two acute angles may vary from 0° to 89°. So, two acute angles of different

measures are not congruent.

91. Two right angles are congruent.

Ans: True

92. Two figures are congruent, if they have the same shape.

Ans: False

Since, two figures are congruent, if they have the same shape and same size.

93. If the areas of two squares is same, they are congruent.

Ans: True

94. If the areas of two rectangles are the same, they are congruent.

Ans: False

95. If the areas of two circles are the same, they are congruent.

Ans: True

96. Two squares having the same perimeter are congruent.

Ans: True

97. Two circles having the same circumference are congruent.

Ans: True

98. If three angles of two triangles are equal, triangles are congruent.

Ans: False

Since, there is no congruency criterion of three angles.

99. If two legs of a right triangle are equal to two legs of another right triangle,

then the right triangles are congruent.

Ans: True

100. If two sides and one angle of a triangle are equal to the two sides and angle

of another triangle, then the two triangles are congruent.

Ans: False

Two triangles are congruent if two sides and included angle of one triangle are equal

to the two sides and included angle of another triangle.

101. If two triangles are congruent, then the corresponding angles are equal.

Ans: True

102. If two angles and a side of a triangle are equal to two angles and a side of

another triangle, then the triangles are congruent.

Ans: False

If two angles and included side of a triangle are equal to two corresponding angles

and the included side of another triangle, then the triangles are congruent.

103. If the hypotenuse of one right triangle is equal to the hypotenuse of another

right triangle, then the triangles are congruent.

Ans: False

Since, two right triangles are congruent, if hypotenuse and one side of a triangle are

equal to hypotenuse and one side of another triangle.

104. If the hypotenuse and an acute angle of one right triangle are equal to the hypotenuse and an acute angle of another right triangle, then the triangles are congruent.

Ans: True

When hypotenuse and an acute angle of one right triangle are equal to the hypotenuse

and an acute angle of another right triangle, it may be converted it into ‘two angles

and the included side’ form of congruence with the help of angle sum property.

105. AAS congruence criterion is same as ASA congruence criterion.

Ans: False

106. In the given figure, AD ⊥ BC and AD is the bisector of angle BAC. Then,

$\triangle$ABD ≅ $\triangle$ACD by RHS.

Ans: False

In $\triangle$ABD and $\triangle$ACD,

AD = AD (common)

$\angle$ BAD =  $\angle$ CAD (∵ AD is the bisector of  $\angle$ BAC)

$\angle$ ADB =  $\angle$ ADC (each angle is $90^\circ$, ∵ AD ⊥ BC)

∴ $\triangle$ABD ≅ $\triangle$ACD (By ASA criterion)

107. The measure of three angles of a triangle are in the ratio 5 : 3 : 1. Find the

measures of these angles.

Ans: Let the angles of the triangle be 5x, 3x and x.

∴ x + 3x + 5x = $180^\circ$ (Angle sum property of a triangle)

$\Rightarrow 9{\text{x }} = {\text{ }}180^\circ$

$\Rightarrow {\text{x }} = \frac{{180^\circ }}{9}$

$\Rightarrow {\text{x }} = 20^\circ$
Thus, 

3x = 3 × $20^\circ$ = $60^\circ$

5x = 5 × $20^\circ$ = $100^\circ$

Thus, angles of the triangle are $100^\circ$, $60^\circ$ and $20^\circ$.

108. In the given figure, find the value of x.

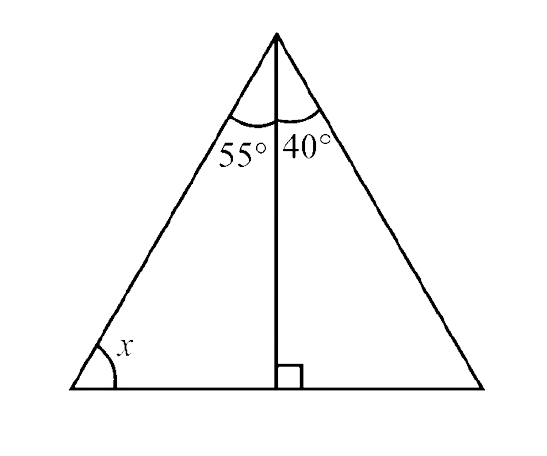
Ans:

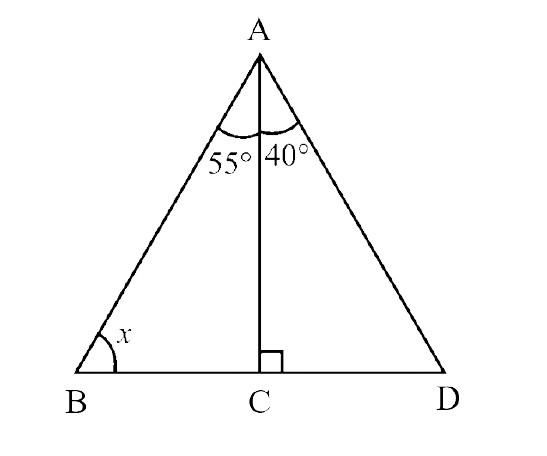
In $\triangle$ABC, 

$\angle$ ACD =  $\angle$ BAC +  $\angle$ ABC (Exterior angle property)

$\Rightarrow$ $90^\circ$ = $55^\circ$ + x

$\Rightarrow$ x = $90^\circ$ – $55^\circ$ = $35^\circ$

Thus, 

x = $35^\circ$

109. In the given figure (i) and (ii), find the values of a, b and c.

(i)

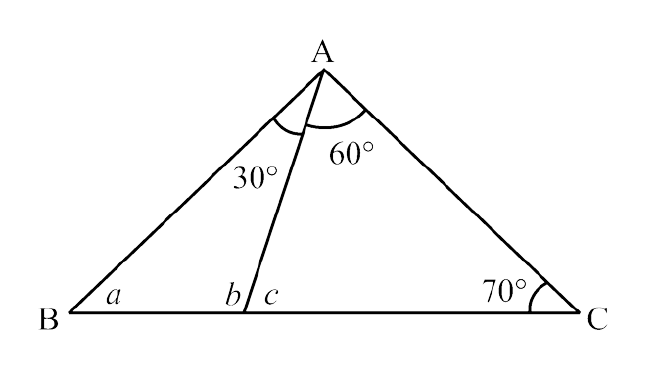
Ans: In $\triangle$ADC, 

$\angle$ ADB =  $\angle$ DAC+  $\angle$ ACD (By exterior angle property)

$\Rightarrow$ b = $60^\circ$ +$70^\circ$ = 1$30^\circ$ …………(i)

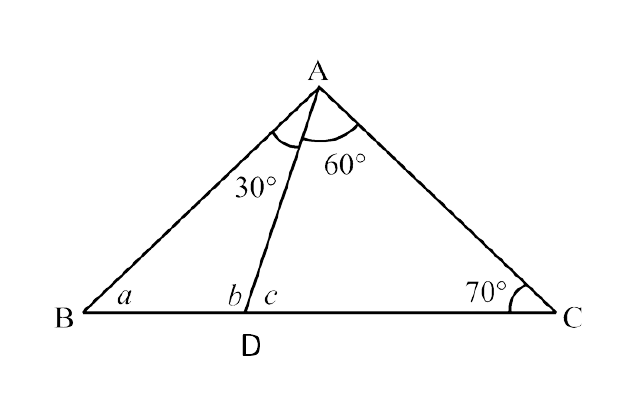
Now, 

In $\triangle$ABD, 

$\angle$ ABD +  $\angle$ ADB +  $\angle$ BAD = $180^\circ$ (By angle sum property)

$\Rightarrow$ a + b + $30^\circ$ = $180^\circ$

$\Rightarrow$ a = $180^\circ$ – $30^\circ$ – 1$30^\circ$ (using equation (i))

$\Rightarrow$ a = $20^\circ$ ………(ii)

Also, 

$\angle$ ADC =  $\angle$ BAD +  $\angle$ ABD (By exterior angle property)

$\Rightarrow$ c = $30^\circ$ + a

$\Rightarrow$ c = $30^\circ$ + $20^\circ$ = $50^\circ$ (using equation(ii))

Thus, 

a = $20^\circ$, b = 1$30^\circ$, c = $50^\circ$

(ii)

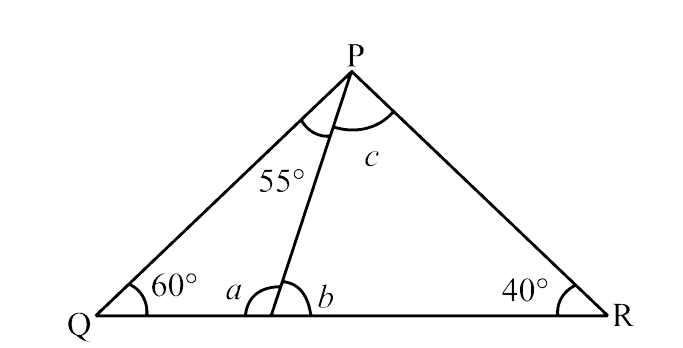
Ans: In $\triangle$PQS, 

$\angle$ PSR =  $\angle$ SPQ +  $\angle$ PQS (By exterior angle property)

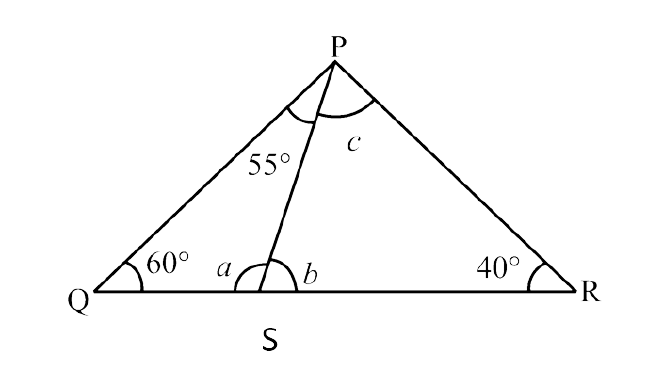
$\Rightarrow$ b = $55^\circ$ + $60^\circ$

$\Rightarrow$ b = 115° …………. (i)

Now, 

In $\triangle$PRS, 

$\angle$ PSR +  $\angle$ PRS +  $\angle$ SPR = $180^\circ$ (By angle sum property)

$\Rightarrow$ b + $40^\circ$ + c = $180^\circ$

$\Rightarrow$ c = $180^\circ$ – $40^\circ$ – 115° (using equation (i))

$\Rightarrow$ c = $25^\circ$ ………. (ii)

Also, 

$\angle$ PSQ =  $\angle$ SPR +  $\angle$ SRP (By exterior angle property)

$\Rightarrow$ a = c + $40^\circ$

$\Rightarrow$ a = $25^\circ$ + $40^\circ$ = 65° (using (ii))

Thus, a = 65°, b = 115°, c = $25^\circ$.

110. In triangle XYZ, the measure of angle X is $30^\circ$ greater than the measure

of angle Y and angle Z is a right angle. Find the measure of  $\angle$ Y.

Ans: Given that

$\angle$ X =  $\angle$ Y + $40^\circ$ ………. (i)

$\angle$ Z = $90^\circ$ ………. (ii)

In $\triangle$XYZ,

$\angle$ X +  $\angle$ Y+ $\angle$ Z = $180^\circ$ (Angle sum property)

$\Rightarrow$  $\angle$ Y + $30^\circ$ +  $\angle$ Y + $90^\circ$ = $180^\circ$ (Using (i) and (ii))

$\Rightarrow$ 2  $\angle$ Y = $180^\circ$ – $90^\circ$ – $30^\circ$ = $60^\circ$

\[\Rightarrow \angle Y = \frac{{60^\circ }}{2} = 30^\circ \]

111. In a triangle ABC, the measure of angle A is $40^\circ$ less than the measure of angle B and 50% less than that of angle C. Find the measure of  $\angle$ A.

Ans: Given that  $\angle$ A =  $\angle$ B – $40^\circ$ …………. (i)

and  $\angle$ A =  $\angle$ C – $50^\circ$ …………..(ii)

Now, in $\triangle$ABC

$\angle$ A +  $\angle$ B +  $\angle$ C = $180^\circ$ (By angle sum property)

$\Rightarrow$  $\angle$ A +  $\angle$ A + $40^\circ$ +  $\angle$ A + $50^\circ$ = $180^\circ$ (Using equation (i) and (ii))

$\Rightarrow$ 3 $\angle$ A + $90^\circ$ = $180^\circ$

$\Rightarrow 3\angle {\text{A }} = {\text{ }}180^\circ -90^\circ  = {\text{ }}90^\circ$

$\Rightarrow \angle {\text{A}} = {\text{ }}\frac{{90^\circ }}{3}$

$\Rightarrow \angle {\text{A}} = 30^\circ$ 

112. I have three sides. One of my angle measures 15°. Another has a measure

of $60^\circ$. What kind of a polygon am I? If I am a triangle, then what kind of

triangle am I?

Ans: A polygon having three sides is a triangle.

Given that the two angles are of measure 15° and $60^\circ$

Let the third angle of the triangle be x.

∴ 15° + $60^\circ$ + x = $180^\circ$ (By angle sum property of a triangle)

$\Rightarrow$ x = $180^\circ$ – $60^\circ$ – 15°

$\Rightarrow$ x = 105°

Thus, one angle of the triangle is an obtuse angle. 

So, a triangle is an obtuse-angled triangle.

113. Jiya walks 6 km due east and then 8 km due north. How far is she from

her starting place?

Ans: Let A be the starting point and B be the ending point of Jiya.

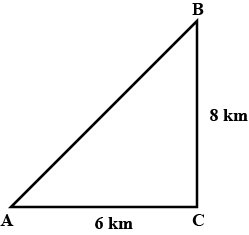
Since $\triangle$ABC is right angled.

∴ (AB)2 = (AC)2 + (BC)2

$\Rightarrow$ (AB)2 = 62 + 82 = 36 + 64 = 100

$\Rightarrow$ AB = 10

Thus, Jiya is 10 km away from her starting place.

114. Jayanti takes shortest route to her home by walking diagonally across a

rectangular park. The park measures 60 metres × 80 metres. How much shorter

Is the route across the park better than the route around its edges?

Ans: Let $\triangle$BCD be the given rectangular park.

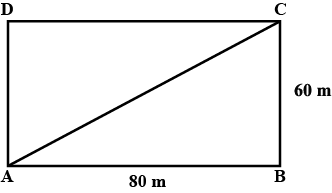
Since, $\triangle$ABC is right angled.

∴ (AC)2 = (AB)2 + (BC)2

$\Rightarrow$ (AC)2 = (80)2 + (60)2 = 6400 + 3600 = 10000

$\Rightarrow$ AC = 100 .

∴ Length of route across the park = 100 m 

And length of route around the edges = (80 + 60) m = 140 m

Thus, the route across the park is shorter than the route around edges of park by

140 m – 100 m = 40 m.

115. In the $\triangle$PQR of the given figure, PQ = PR. Find the measures of  $\angle$ Q and  $\angle$ R.

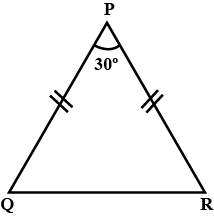
Ans:  $\angle$ PRQ =  $\angle$ PQR (∵ PQ = PR (given))

Now, in $\triangle$PQR

$\angle$ PQR +  $\angle$ PRQ+  $\angle$ QPR = $180^\circ$ (Angle sum property)

$\Rightarrow$ 2 $\angle$ PQR + $30^\circ$ = $180^\circ$ (using (i))

$\Rightarrow$ 2 $\angle$ PQR = $180^\circ$ – $30^\circ$ = 1$50^\circ$

\[\Rightarrow \angle {\text{PQR}} = \frac{{150^\circ }}{2} = 75^\circ \]

Thus,  $\angle$ Q =  $\angle$ R = $75^\circ$.

116. In the given figure, find the measures of angles x and y.

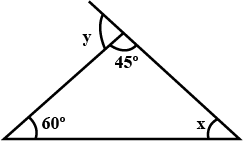
Ans:

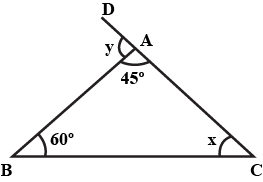
In $\triangle$ABC,

$\angle$ BAC +  $\angle$ ABC +  $\angle$ ACB = $180^\circ$ (Angle sum property)

$\Rightarrow$ $45^\circ$ + $60^\circ$ + x = $180^\circ$

$\Rightarrow$ x = $180^\circ$ – $45^\circ$ – $60^\circ$ = $75^\circ$ ……………. (i)

Now, 

$\angle$ BAD = $\angle$ ABC +  $\angle$ ACB (By exterior angle property)

$\Rightarrow$ y = $60^\circ$ + x

$\Rightarrow$ y = $60^\circ$ + $75^\circ$ = 1$35^\circ$ (using equation (i))

Thus, x = $75^\circ$ and y = 1$35^\circ$

117. In the given figure, find the measures of  $\angle$ PON and  $\angle$ NPO.

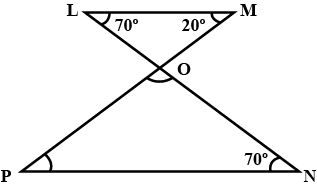
Ans: In $\triangle$LOM,

$\angle$ LOM +  $\angle$ OLM+ $\angle$ OML = $180^\circ$ (By angle sum property)

$\Rightarrow$  $\angle$ LOM + $70^\circ$ + $20^\circ$ = $180^\circ$

$\Rightarrow$  $\angle$ LOM = $180^\circ$ – $70^\circ$ – $20^\circ$ = $90^\circ$

$\angle$ LOM =  $\angle$ PON (Vertically opposite angles)

∴  $\angle$ PON = $90^\circ$

Now, in $\triangle$ΡΟΝ,

 $\angle$ PON +  $\angle$ ONP +  $\angle$ NPO = $180^\circ$ (Angle sum property)

$\Rightarrow$ $90^\circ$ + $70^\circ$ +  $\angle$ NPO = $180^\circ$

$\Rightarrow$  $\angle$ NPO = $180^\circ$ –  $90^\circ$ – $70^\circ$ = $20^\circ$

Thus,  $\angle$ PON = $90^\circ$ and  $\angle$ NPO = $20^\circ$

118. In the given figure QP || RT. Find the values of x and y.

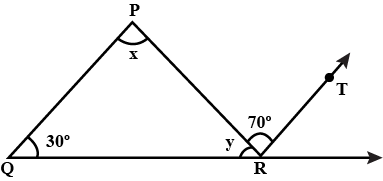
Ans: QP || RT and PR is a transversal.

∴  $\angle$ QPR =  $\angle$ PRT (Alternate interior angles)

$\Rightarrow$ x = $70^\circ$

Now, OP || RT and OR is a transversal.

∴  $\angle$ PQR +  $\angle$ QRT = $180^\circ$ (Co-interior angles)

$\Rightarrow$ $30^\circ$ + y + $70^\circ$ = $180^\circ$

$\Rightarrow$ y = $180^\circ$ – $30^\circ$ – $70^\circ$ = $80^\circ$

Thus, a = $70^\circ$ and y = $80^\circ$,

119. Find the measure of  $\angle$ A in the given figure.

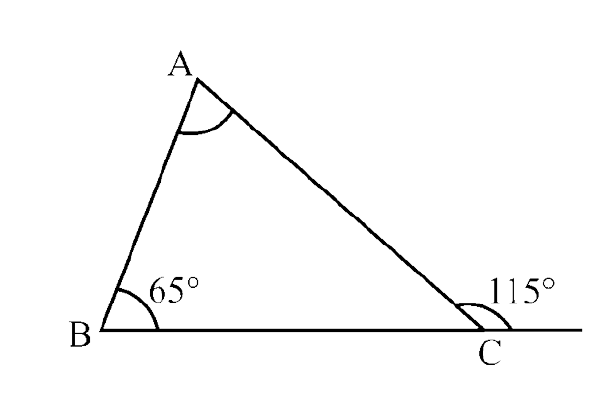
Ans:

$\angle$ ACD =  $\angle$ ABC +  $\angle$ CAB (By exterior angle property)

$\Rightarrow$ 115° = 65° +  $\angle$ CAB

$\Rightarrow$  $\angle$ CAB = 115° – 65°= $50^\circ$

Thus,  $\angle$ A = $50^\circ$

120. In a right-angled triangle if an angle measures $35^\circ$, then find the measure

of the third angle.

Ans: Let $\triangle$ABC be the given triangle such that  $\angle$ B = $90^\circ$ and  $\angle$ C = $35^\circ$

Now, 

$\angle$ A + $\angle$ B +  $\angle$ C = $180^\circ$ (By angle sum property)

$\Rightarrow$  $\angle$ A = $180^\circ$ – $90^\circ$ – $35^\circ$

$\Rightarrow$  $\angle$ A = $55^\circ$

Thus, the third angle of the triangle is $55^\circ$.

121. Each of the two equal angles of an isosceles triangle is four times the third

angle. Find the angles of the triangle.

Ans: Let $\triangle$ABC be the given isosceles triangle, such that AB = AC and  $\angle$ B =  $\angle$ C = x.

Now,  $\angle$ B =  $\angle$ C = 4 $\angle$ A ………. (i) (given)

$\angle$ A + $\angle$ B + $\angle$ C = $180^\circ$ (By angle sum property)

$\Rightarrow$  $\angle$ A + 4  $\angle$ A + 4  $\angle$ A = $180^\circ$ (Using equation (i))

 $\Rightarrow 9\angle A{\text{ }} = {\text{ }}180^\circ$

 $\Rightarrow \angle A = \frac{{180^\circ }}{9} = 20^\circ$
∴  $\angle$ B =  $\angle$ C = 4 × $20^\circ$ = $80^\circ$

Thus, $20^\circ$, $80^\circ$ and $80^\circ$ are the angles of the triangle.

122. The angles of a triangle are in the ratio 2 : 3 : 5. Find the angles.

Ans: Let the angles of the triangle be 2x, 3x and 5x.

∴ 2x + 3x + 5x = $180^\circ$ (Angle sum property of a triangle)

 $\Rightarrow 10x{\text{ }} = {\text{ }}180^\circ$

 $\Rightarrow x = \frac{{180^\circ }}{{10}} = 18^\circ$ 

∴ 2x = 2 × 18° = 36°, 

3x = 3 × 18° = 54°, 

5x = 5 × 18°= $90^\circ$

Thus, 36°, 54° and $90^\circ$are the angles of the triangle.

123. If the sides of a triangle are produced in an order, show that the sum of the

exterior angles so formed is 3$60^\circ$.

Ans: Let $\triangle$ABC be the given triangle and BD, CE, AF are the produced side in order

By exterior angle property,

$\angle$ ACD =  $\angle$ CAB +  $\angle$ CBA ………. (i) 

$\angle$ BAE =  $\angle$ ABC +  $\angle$ ACB ……… (ii) 

$\angle$ CBF =  $\angle$ BAC +  $\angle$ BCA ……….(iii) 

Add equations (i), (ii) and (iii),

$\angle$ ACD +  $\angle$ BAE + $\angle$ CBF =  $\angle$ CAB + $\angle$ CBA +  $\angle$ ABC +  $\angle$ ACB +  $\angle$ BAC +  $\angle$ BCA

So, 

$\angle ACD{\text{ }} + \angle BAE{\text{ }} + \angle CBF{\text{ }} = {\text{ }}2(\angle ABC{\text{ }} + \angle ACB{\text{ }} + \angle BAC)$ 

$= {\text{ }}2(180^\circ ){\text{ }}\left( {{\text{Angle sum property}}} \right)$ 

$= {\text{ }}360^\circ$ 

124. In $\triangle$ABC, if  $\angle$ A =  $\angle$ C, and exterior angle ABX = 1$40^\circ$, then find the angles

of the triangle.

Ans:  $\angle$ ABX= $\angle$ BAC +  $\angle$ BCA (Exterior angle property)
$\Rightarrow$ 1$40^\circ$ = 2 $\angle$ BAC (∵  $\angle$ A =  $\angle$ C)

\[\angle BAC = \frac{{140^\circ }}{2} = 70^\circ \]

∴ BAC = $\angle$ BCA = $70^\circ$ ……… (i)

Now, in $\triangle$ABC

$\angle$ A + $\angle$ B +  $\angle$ C = $180^\circ$ (Angle sum property)

$\Rightarrow$  $\angle$ B = $180^\circ$ – $70^\circ$ – $70^\circ$ (Using equation (i))

$\Rightarrow$  $\angle$ B = $40^\circ$

Thus,  $\angle$ A = $70^\circ$,  $\angle$ B = $40^\circ$ and  $\angle$ C = $70^\circ$ are the angles of the triangle.

125. Find the values of x and y in the given figure.

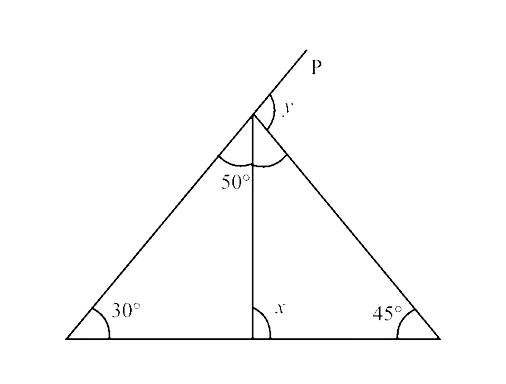
Ans: In $\triangle$QRS, 

 $\angle$ QST =  $\angle$ QRS +  $\angle$ SOR (Exterior angle property)

$\Rightarrow$ x = $30^\circ$ + $50^\circ$ = $80^\circ$

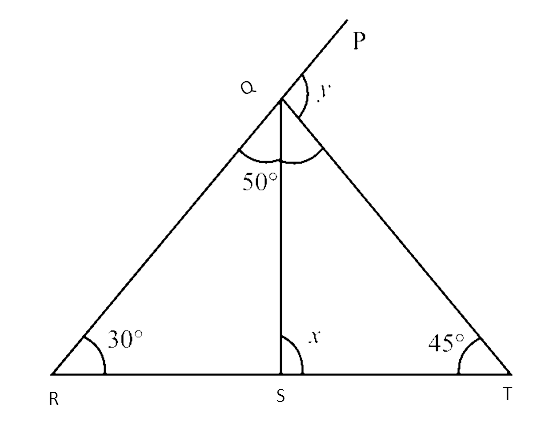
Also, in $\triangle$QRT, 

$\angle$ PQT =  $\angle$ QRT +  $\angle$ QTR (By exterior angle property)

$\Rightarrow$ y = $30^\circ$ + $45^\circ$ = $75^\circ$

Thus, x = $80^\circ$ and y = $75^\circ$

126. Find the value of x in the given figure.

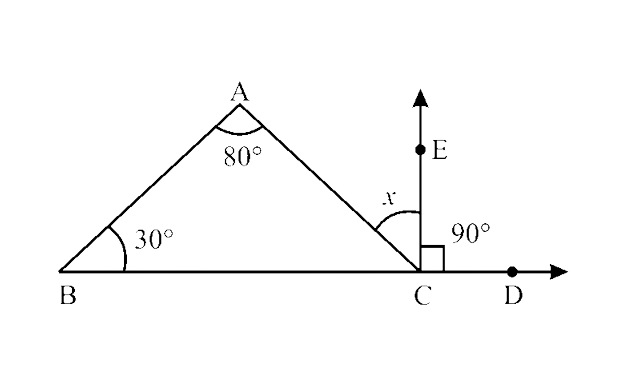
Ans: In $\triangle$ABC, 

 $\angle$ ACD=  $\angle$ CAB +  $\angle$ CBA (By exterior angle property)

$\Rightarrow$ x + $90^\circ$ = $80^\circ$ + $30^\circ$

$\Rightarrow$ x = $110^\circ$ – $90^\circ$ 

$\Rightarrow$ x = $20^\circ$

127. The angles of a triangle are arranged in descending order of their magnitudes. If the difference between two consecutive angles is 10, find the three angles.

Ans: Let $\triangle$ABC be the given triangle and descending order of angles of the triangle

is  $\angle$ A,  $\angle$ B,  $\angle$ C.

Now, 

$\angle$ A –  $\angle$ B = $10^\circ$ ………. (i)

$\angle$ B –  $\angle$ C = $10^\circ$ ………. (ii)

Also, 

$\angle$ A + $\angle$ B +  $\angle$ C = $180^\circ$ (By angle sum property)

$\Rightarrow$  $\angle$ B + $10^\circ$ +  $\angle$ B +  $\angle$ B – $10^\circ$ = $180^\circ$ (Using equations (i) and (ii))

$\Rightarrow 3\angle B{\text{ }} = {\text{ }}180^\circ$

$\Rightarrow \angle B = \frac{{180^\circ }}{3}$

$\Rightarrow \angle B = 60^\circ$
Thus,

$\angle$ A =  $\angle$ B + $10^\circ$ = $60^\circ$ + $10^\circ$ = $70^\circ$

And 

$\angle$ C =  $\angle$ B – $10^\circ$ = $60^\circ$ – $10^\circ$ = $50^\circ$

Thus, $70^\circ$, $60^\circ$ and $50^\circ$ are the angles of the triangle.

128. In $\triangle$ABC, DE || BC (see figure). Find the values of x,y and z.

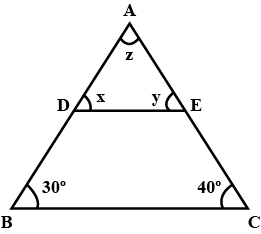
Ans:

DE || BC and AB is a transversal.

∴  $\angle$ ADE =  $\angle$ DBC (Corresponding angles)

$\Rightarrow$ x= $30^\circ$

Now, DE || BC and AC is a transversal.

∴  $\angle$ AED =  $\angle$ ECB (Corresponding angles)

$\Rightarrow$ y = $40^\circ$

In $\triangle$ABC,

$\angle$ A +  $\angle$ B +  $\angle$ C = $180^\circ$ (By angle sum property)

$\Rightarrow$ z + $30^\circ$ + $40^\circ$ = $180^\circ$

$\Rightarrow$ z = $180^\circ$ – $40^\circ$ – $30^\circ$ = $110^\circ$

Thus, x = $30^\circ$, y = $40^\circ$ and z = $110^\circ$.

129. In the given figure, find the values of x, y and z.

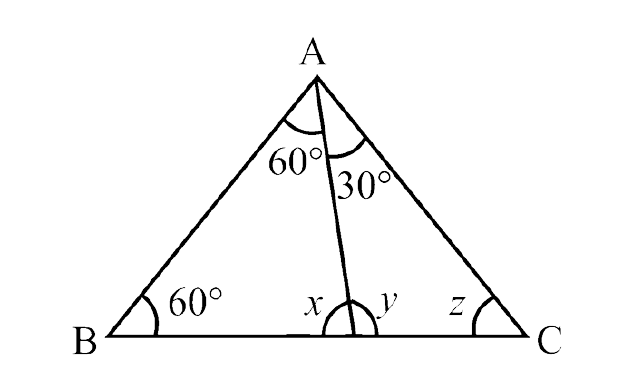
Ans: In $\triangle$ABD,

$\angle$ BAD +  $\angle$ BDA +  $\angle$ ABD = $180^\circ$ (Angle sum property)

$\Rightarrow$ $60^\circ$ + x + $60^\circ$ = $180^\circ$

$\Rightarrow$ x = $180^\circ$ – $120^\circ$ = $60^\circ$

Now, 

$\angle$ ADC =  $\angle$ BAD +  $\angle$ ABD (By exterior angle property)

$\Rightarrow$ y = $60^\circ$ + $60^\circ$ = $120^\circ$

Also, in $\triangle$ADC,

$\angle$ ADB –  $\angle$ DAC +  $\angle$ DCA (By Exterior angle property)

$\Rightarrow$ x = $30^\circ$ + z

$\Rightarrow$ z = $60^\circ$ – $30^\circ$ = $30^\circ$ (Since x = $60^\circ$)

Therefore, x = $60^\circ$, y = $120^\circ$ and z = $30^\circ$.

130. If one angle of a triangle is $60^\circ$ and the other two angles are in the ratio 1 :

2, find the angles.

Ans: Let $\triangle$ABC be the given triangle such that  $\angle$ A = $60^\circ$ and let angle B and C are

x and 2x respectively.

$\angle$ A +  $\angle$ B +  $\angle$ C = $180^\circ$ (By angle sum property)

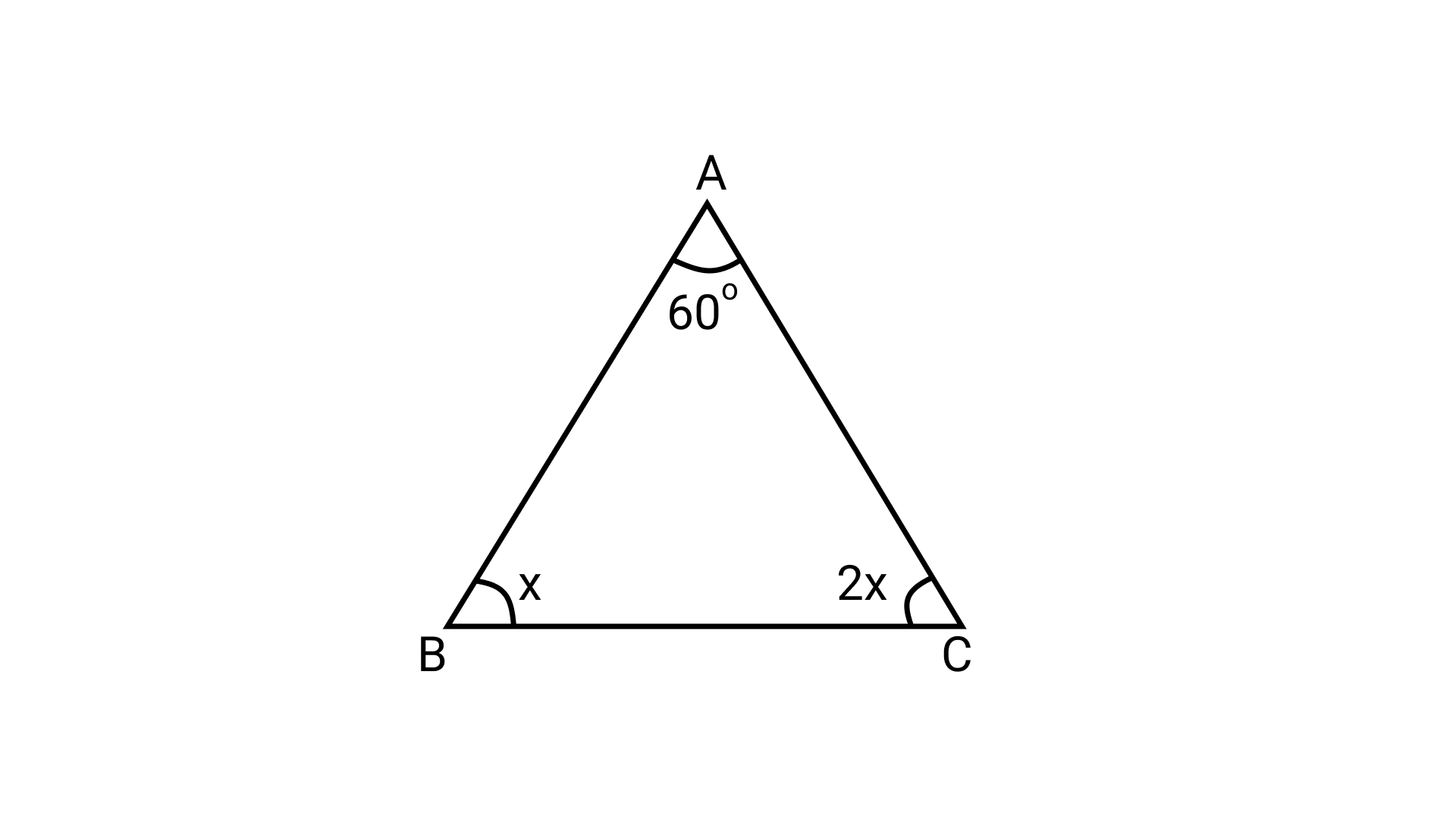
$\Rightarrow 60^\circ  + {\text{ }}x{\text{ }} + {\text{ }}2x{\text{ }} = {\text{ }}180^\circ$

$\Rightarrow 3x{\text{ }} = {\text{ }}180^\circ -60^\circ  = {\text{ }}120^\circ$

$\Rightarrow x = \frac{{120^\circ }}{3} = 40^\circ$ 

Therefore,  $\angle$ B = $40^\circ$ and  $\angle$ C = 2 × $40^\circ$ = $80^\circ$

131. In $\triangle$POR, If 3 $\angle$ P = 4 $\angle$ Q = 6 $\angle$ R, calculate the angles of the triangle.

Ans:  $ 3\angle P = 4\angle Q = 6\angle R\left( {{\text{Given}}} \right)$

$\Rightarrow \angle P = \frac{4}{3}\angle Q$

$\Rightarrow \angle R = \frac{4}{6}\angle Q$ 

$\angle$ P +  $\angle$ Q+  $\angle$ R = $180^\circ$ (By angle sum property)

$\Rightarrow \frac{4}{3}\angle Q + \angle Q + \frac{4}{6}\angle Q = 180^\circ$

$\Rightarrow \frac{4}{3}\angle Q + \angle Q + \frac{2}{3}\angle Q = 180^\circ$

$\Rightarrow \frac{9}{3}\angle Q = 180^\circ$

$\Rightarrow 3\angle Q = 180^\circ$

$\Rightarrow \angle Q = \frac{{180^\circ }}{3} = 60^\circ$ 

So,

$\angle P = \frac{4}{3}\angle Q = \frac{4}{3} \times 60^\circ  = 4 \times 20^\circ  = 80^\circ$

$\angle R = \frac{4}{6}\angle Q = \frac{4}{6} \times 60^\circ  = 4 \times 10^\circ  = 40^\circ$ 

Thus,  $\angle$ P = $80^\circ$,  $\angle$ Q = $60^\circ$ and  $\angle$ R = $40^\circ$.

132. In $\triangle$DEF,  $\angle$ D = $60^\circ$,  $\angle$ E = $70^\circ$ and the bisectors of  $\angle$ E and  $\angle$ F meet at O. Find

(i)  $\angle$ F

Ans: In $\triangle$DEF,

$\angle$ D +  $\angle$ E + $\angle$ F = $180^\circ$ (Angle sum property)

$\Rightarrow$ $60^\circ$ + $70^\circ$ +  $\angle$ F = $180^\circ$

$\Rightarrow$  $\angle$ F = $180^\circ$ – $60^\circ$ – $70^\circ$ = $50^\circ$

(ii)  $\angle$ EOF

Ans: Since, EO and FO are the bisectors of  $\angle$ E and  $\angle$ F respectively.

\[\therefore \;\angle OEF = \angle OED = \frac{{70^\circ }}{2} = 35^\circ \]

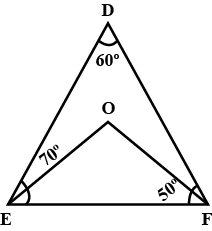
And \[\angle OFE = \angle OFD = \frac{{50^\circ }}{2} = 25^\circ \]

Now, in $\triangle$OEF, 

$\angle$ OEF +  $\angle$ OFE +  $\angle$ EOF = $180^\circ$ (By angle sum property)

$\Rightarrow$ $35^\circ$ + $25^\circ$ +  $\angle$ EOF = $180^\circ$

$\Rightarrow$  $\angle$ EOF = $180^\circ$ – $35^\circ$ – $25^\circ$ = $120^\circ$

133. In the given figure, $\triangle$PQR is right-angled at P.U and Tare the points on

line QRF. If OP || ST and US || RP, find  $\angle$ S.

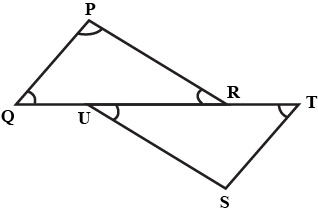
Ans:

QP || ST and QT are transversals.

Therefore,  $\angle$ PQT =  $\angle$ STO (Alternate interior angles)

US || PR and UR is a transversal.

Therefore,  $\angle$ PRU =  $\angle$ SUR (Alternate interior angles)

Two angles of $\triangle$PQR equal to two angles of $\triangle$STU. 

Thus, the third angle also will be equal.

$\Rightarrow$  $\angle$ QPR =  $\angle$ TSU

Now, it is given that  $\angle$ P = $90^\circ$.

Hence,  $\angle$ S = $90^\circ$.

134. In each of the given pairs of triangles of figure, applying only ASA

congruence criterion, determine which triangles are congruent. Also, write the

congruent triangles in symbolic form.

(a) 

Ans: In the given figure, 

$\triangle$ABC and $\triangle$POR are not congruent.

(b) 

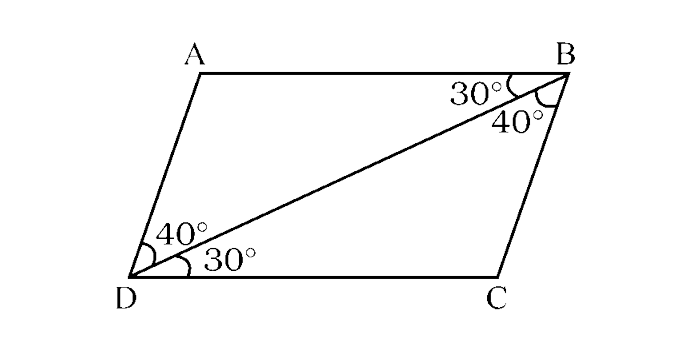
Ans: In $\triangle$ABD and $\triangle$CDB,

BD = DB (common)

$\angle$ ABD = $\angle$ CDB = $30^\circ$ (given)

$\angle$ ADB =  $\angle$ CBD = $40^\circ$ (given)

So, $\triangle$ABD ≅ $\triangle$CDB (By ASA criterion)

(c) 

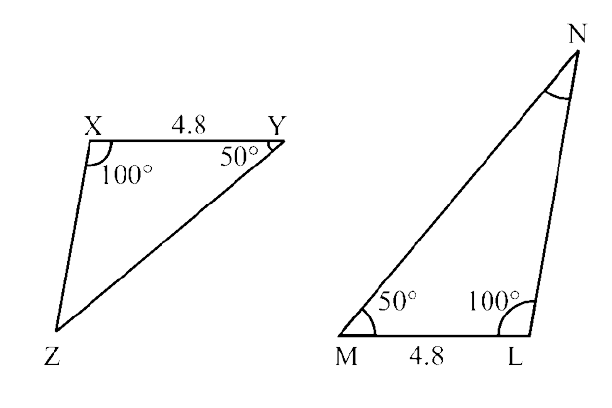
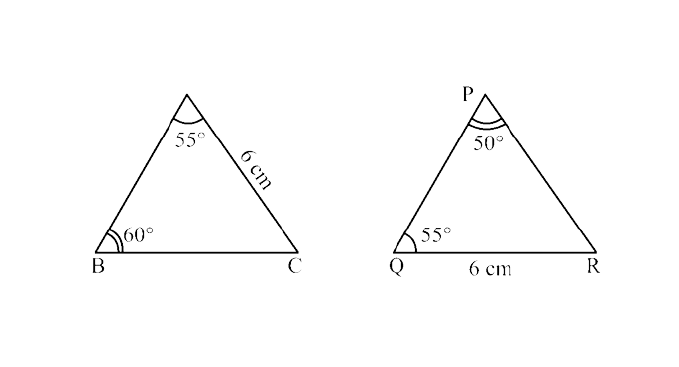
Ans: In $\triangle$XYZ and $\triangle$LMN,

XY = LM = 4.8 (given)

$\angle$ YXZ =  $\angle$ MLN – $100^\circ$ (given)

$\angle$ XYZ = LMN = $50^\circ$ (given)

So, $\triangle$XYZ ≅ $\triangle$LMN (By ASA criterion)
(d) 

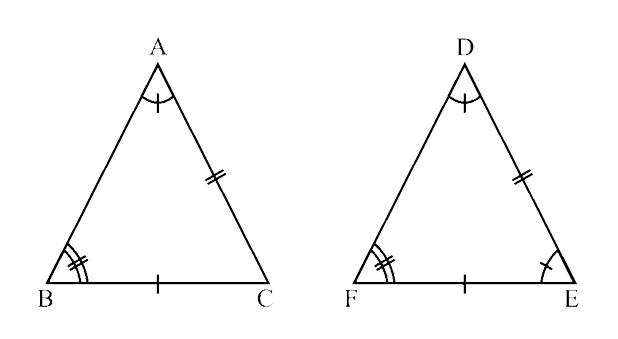
Ans: In $\triangle$ABC and $\triangle$DFE,

$\angle$ A = $\angle$ D (given)

$\angle$ B =  $\angle$ F (given)

∴  $\angle$ C =  $\angle$ E (since other two angles are equal)

BC = FE (given)

So, $\triangle$ABC ≅ $\triangle$DFE (By ASA criterion)

(e)

Ans: In $\triangle$PON and $\triangle$MNO,

NO = ON (common)

 $\angle$ NOP =  $\angle$ ONM = $50^\circ$ + 40 = $90^\circ$ (given)

 $\angle$ ONP =  $\angle$ NOM = $50^\circ$ (given)

So, $\triangle$PON ≅ $\triangle$MNO (By ASA criterion)

(f) 

Ans: In $\triangle$AOD and $\triangle$BOC,

$\angle$ AOD =  $\angle$ BOC (Vertically opposite angles)

OD = OC (given)

$\angle$ ADO =  $\angle$ BCO (given)

So, $\triangle$AOD ≅ $\triangle$BOC (By ASA criterion)

135. In each of the given pairs of triangles of figure, using only RHS congruence

criterion, determine which pairs of triangles are congruent. In case of

congruence, write the result in symbolic form:

(a) 

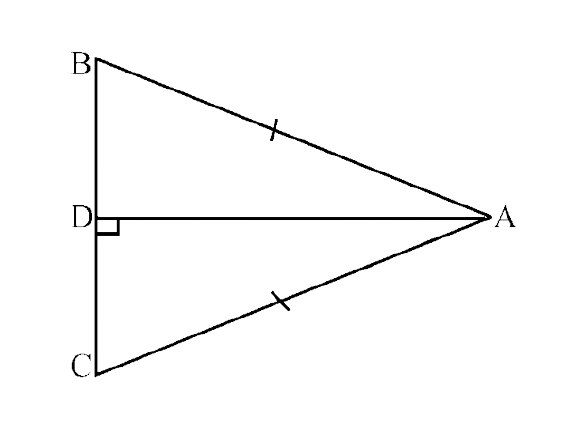
Ans: In $\triangle$ADB and $\triangle$ADC,

AD = AD (common)

$\angle$ ADB =  $\angle$ ADC (Each $90^\circ$)

AB = AC (given hypotenuse)

So, $\triangle$ADB ≅ $\triangle$ADC (By RHS criterion)

(b) 

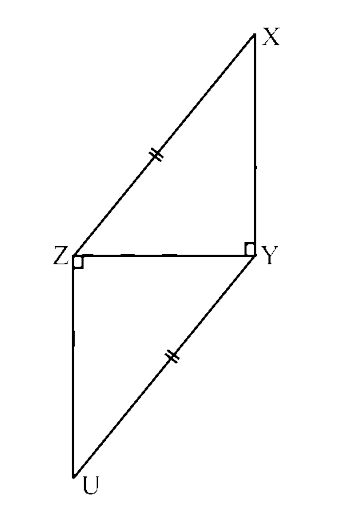
Ans: In $\triangle$XYZ and $\triangle$UZY,

 $\angle$ Y =  $\angle$ Z (Each $90^\circ$)

XZ = UY (given hypotenuse)

YZ = ZY (common)

So, $\triangle$XYZ ≅ $\triangle$UZY (By RHS criterion)

(c) 

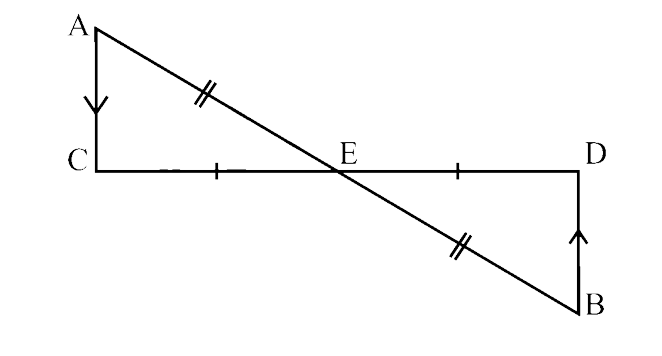
Ans: In $\triangle$ACE and $\triangle$BDE,

$\angle$ ACE =  $\angle$ BDE (AC || BD, alternate interior angles)

CE = DE (given)

 $\angle$ AEC =  $\angle$ BED (Vertically opposite angles)

So, $\triangle$ACE ≅ $\triangle$BDE (By ASA criterion)

Therefore, triangles are congruent but not by RHS congruence criterion.

(d) 

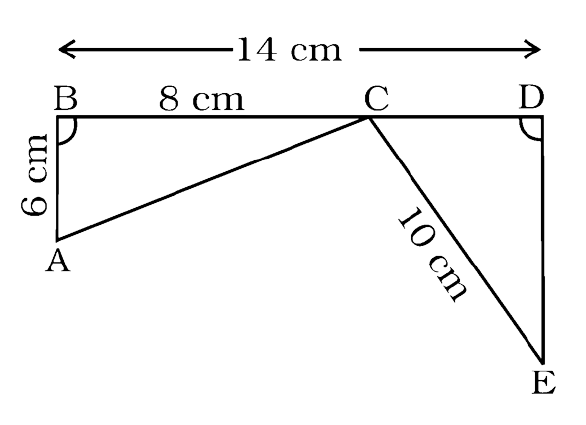
Ans: In $\triangle$ABC, 

By Pythagoras theorem

${\left( {AC} \right)^2}\; = {\text{ }}{\left( {AB} \right)^2}\; + {\text{ }}{\left( {BC} \right)^2}$

${\left( {AC} \right)^2} = {\text{ }}{6^2}\; + {\text{ }}{8^2}$

${\left( {AC} \right)^2} = {\text{ }}36{\text{ }} + {\text{ }}64{\text{ }}$

${\left( {AC} \right)^2} = {\text{ }}100{\text{ }}$

$AC = {\text{ }}{10^2}$

$\therefore AC = 10{\text{ cm}}$ 

In $\triangle$EDC,

DC = BD – BC = (14 – 8) cm = 6cm, 

CE = 10 cm

Now, 

In $\triangle$ABC and $\triangle$CDE,

$\angle$ B = $\angle$ D (each $90^\circ$)

AB = CD = 6 cm

AC = CE = 10 cm (Hypotenuse)

So, $\triangle$ABC ≅ $\triangle$CDE (By RHS criterion)

(e) 

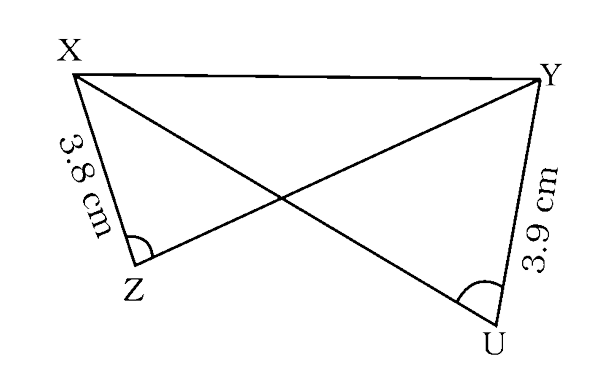
Ans: In the given figure, $\triangle$XYZ and $\triangle$YXU are not congruent by any criterion.

(f) 

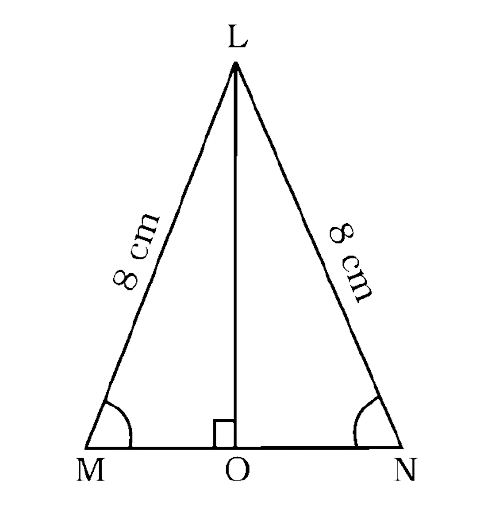
Ans: In $\triangle$LMO and $\triangle$LNO,

LO = LO (common)

LM = LN = 8 cm (hypotenuse)

$\angle$ LOM =  $\angle$ LON (each $90^\circ$)

So, $\triangle$LOM ≅ $\triangle$LON (By RHS criterion)

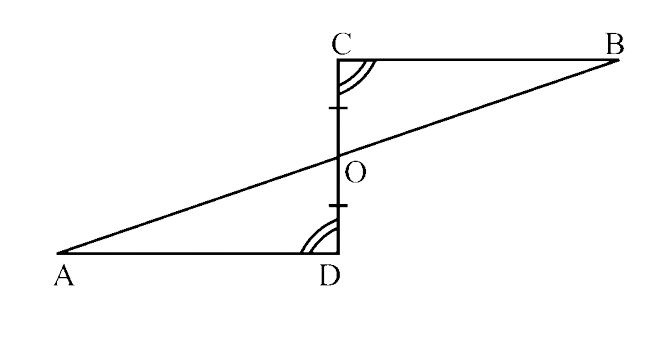
136. In the given figure, if RP=RQ, find the value of x.

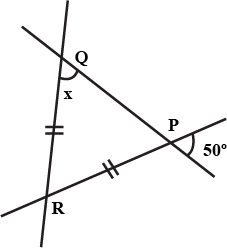
Ans: RP = RQ

∴  $\angle$ RQP =  $\angle$ RPQ = x (angles opposite to equal sides are equal)

Now,  $\angle$ RPQ = $50^\circ$ (vertically opposite angles)

$\Rightarrow$ x = $50^\circ$

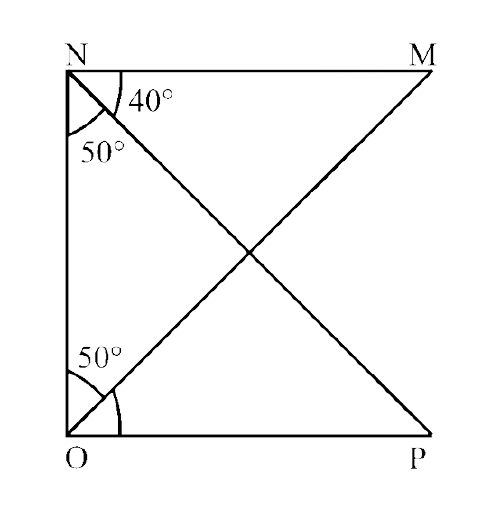
137. In the given figure, if ST = SU, then find the values of x and y.

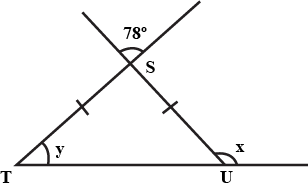
Ans:  $\angle$ TSU = $78^\circ$ (vertically opposite angles)

$\angle$ SUT =  $\angle$ STU = y (Since ST = SU)

Now, in $\triangle$STU,

$\angle$ STU +  $\angle$ SUT +  $\angle$ TSU = $180^\circ$ (By angle sum property)

$\Rightarrow y{\text{ }} + {\text{ }}y{\text{ }} + {\text{ }}78^\circ  = {\text{ }}180^\circ$

$\Rightarrow 2y{\text{ }} = {\text{ }}180^\circ -78^\circ  = {\text{ }}102^\circ$

$\Rightarrow y = \frac{{102^\circ }}{2} = 51^\circ$ 

Now, x =  $\angle$ TSU +  $\angle$ UTS (By exterior angle property)

$\Rightarrow$ x = $78^\circ$ + 51°

$\Rightarrow$ x = 129°

Therefore, x = 129° and y = 51°.

138. Check whether the following measures (in cm) can be the sides of a right angled triangle or not. 1.5, 3.6, 3.9

Ans: Here, \[{\left( {1.5} \right)^2}\; + {\text{ }}{\left( {3.6} \right)^2}\; = {\text{ }}2.25{\text{ }} + {\text{ }}12.96{\text{ }} = {\text{ }}15.21\]

And  \[{\left( {3.9} \right)^2}\; = {\text{ }}15.21\]
Thus, 

\[{\left( {1.5} \right)^2}\; + {\text{ }}{\left( {3.6} \right)^2}\; = {\text{ }}{\left( {3.9} \right)^2}\]

Yes, given sides are sides of a right-angled triangle.

139. Height of a pole is 8 m. Find the length of rope tied with its top from a point on the ground at a distance of 6 m from its bottom.

Ans: Let AB be the given pole of height 8m and rope be AC.

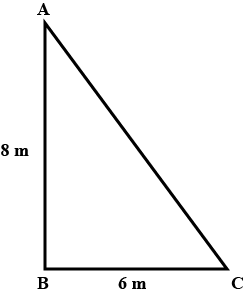
Since, $\triangle$ABC is a right angled triangle.

Use Pythagoras Theorem, 

${\left( {AC} \right)^2}\; = {\text{ }}{\left( {AB} \right)^2}\; + {\text{ }}{\left( {BC} \right)^2}$

${\left( {AC} \right)^2}\; = {\text{ }}{8^2}\; + {\text{ }}{6^2}\; = {\text{ }}64{\text{ }} + {\text{ }}36$

${\left( {AC} \right)^2}\; = {\text{ }}100{\text{ }} = {\text{ }}{10^2}$

$\therefore AC{\text{ }} = {\text{ }}10{\text{ m}}$ 

Thus, the required length of rope is 10 m.

140. In the given figure, if y is five times x, find the value of z.

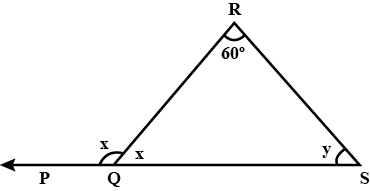
Ans: In $\triangle$QRS,

$\angle$ ROS +  $\angle$ RSQ +  $\angle$ QRS = $180^\circ$ (Angle sum property)

$\Rightarrow$ x + y + $60^\circ$ = $180^\circ$

$\Rightarrow$ x + 5x = $180^\circ$ – $60^\circ$ (Since y = 5x (given))

$\Rightarrow 6x{\text{ }} = {\text{ }}120^\circ$

$\Rightarrow x = \frac{{120^\circ }}{5} = 20^\circ$ 

So, y = 5x = 5 × $20^\circ$ – $100^\circ$

Now, 

$\angle$ RQP =  $\angle$ QRS +  $\angle$ QSR (By exterior angle property)

$\Rightarrow$ z = $60^\circ$ + $100^\circ$ 

$\Rightarrow$ z = 1$60^\circ$

141. The lengths of two sides of an isosceles triangle are 9 cm and 20 cm. What is the perimeter of the triangle? Give a reason.

Ans: Sides of isosceles triangle are 9 cm and 20 cm.

Since, the sum of any two sides of a triangle is greater than the third side.

If third side will be 9 cm then 9 + 9 = 18 < 20

Hence, the triangle will not form.

So, the third side of the triangle must be 20 cm.

Perimeter = (9 + 20 + 20) cm = 49 cm.

142. Without drawing the triangles write all six pairs of equal measures in each of the following pairs of congruent triangles.

(a) $\triangle$STU ≅ $\triangle$DEF 

Ans: $\triangle$STU ≅ $\triangle$DEF

ST = DE, TU= LF, SU = DF

$\angle$ STU =  $\angle$ DEF,  $\angle$ SUT =  $\angle$ DFE,  $\angle$ TSU =  $\angle$ EDF

(b) $\triangle$ABC ≅ $\triangle$LMN

Ans: $\triangle$ABC ≅ $\triangle$LMN

AB = LM, BC = MN, AC = LN

$\angle$ ABC =  $\angle$ LMN,  $\angle$ ACB =  $\angle$ ANM,  $\angle$ BAC = $\angle$ MLN

(c) $\triangle$YZX ≅ $\triangle$POR

Ans: $\triangle$YZX ≅ $\triangle$POR

YZ = PQ, ZX = OR, YX = PR

$\angle$ YZX = $\angle$ POR,  $\angle$ YXZ =  $\angle$ PRO,  $\angle$ XYZ =  $\angle$ RPQ

(d) $\triangle$XYZ ≅ $\triangle$MLN

Ans: $\triangle$XYZ ≅ $\triangle$MLN

XY = ML, YZ = LN, XZ = MN

$\angle$ XYZ =  $\angle$ MLN,  $\angle$ XZY =  $\angle$ MNL,  $\angle$ ZXY =  $\angle$ NML.

143. In the following pairs of triangles of figure, the lengths of the sides are

indicated along the sides. By applying SSS congruence criterion, determine

which triangles are congruent. If congruent, write the results in symbolic form.

(a) 

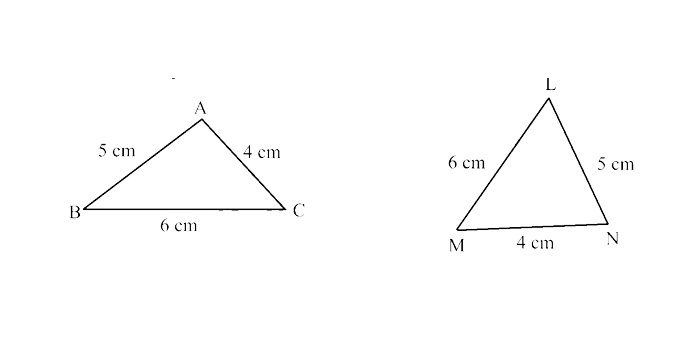
Ans: In $\triangle$ABC and $\triangle$NLM,

AB = NL = 5 cm (given)

BC = LM = 6 cm (given)

AC = NM = 4 cm (given)

∴ $\triangle$ABC ≅ $\triangle$NLM (SSS criterion)

(b) 

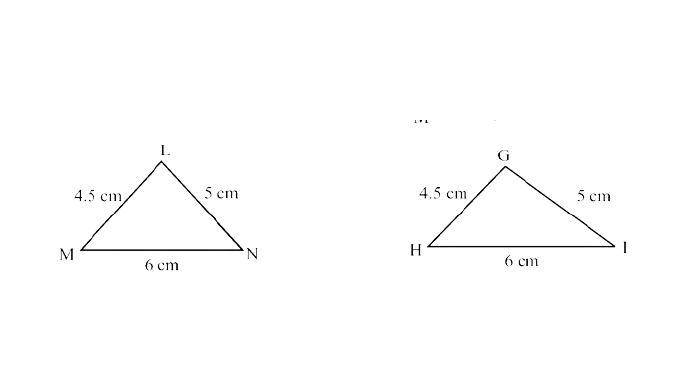
Ans: In $\triangle$LMN and $\triangle$GHI,

LM = GH = 4.5 cm (given)

LN = GI = 5 cm (given)

MN = HI = 6 cm (given)

∴ $\triangle$LMN ≅ $\triangle$GHI (SSS criterion)

(c) 

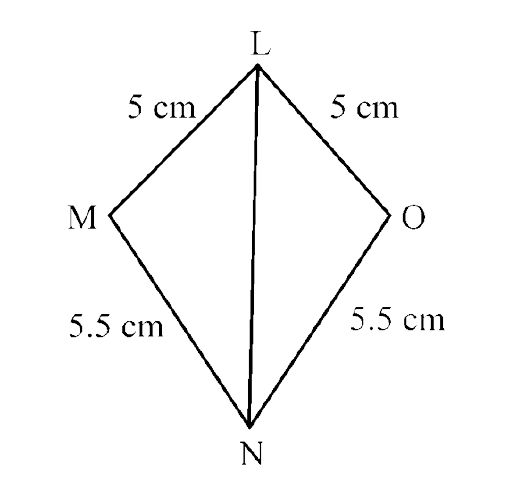
Ans: In $\triangle$LMN and $\triangle$LON,

LM = LO = 5 cm (given)

MN = ON = 5.5 cm (given)

LN = LN (common)

So, $\triangle$LMN ≅ $\triangle$LON (By SSS criterion)

(d) 

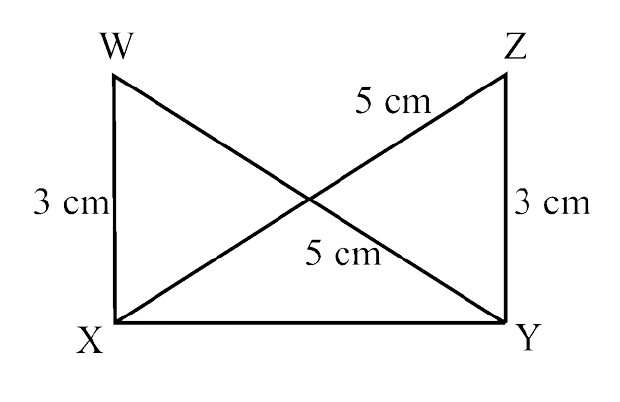
Ans: In $\triangle$XYZ and $\triangle$YXW,

XY = YX (common)

ZY = WX = 3 cm (given)

ZX = WY = 5 cm (given)

So, $\triangle$YXW ≅ $\triangle$XYZ (By SSS criterion)

(e) 

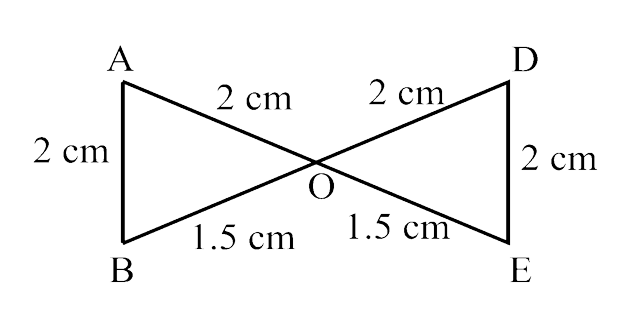
Ans: In $\triangle$AOB and $\triangle$DOE,

AO = DO = 2 cm (given)

AB = DE = 2 cm (given)

BO = EO = 1.5 cm (given)

So, $\triangle$AOB ≅ $\triangle$DOE (By SSS criterion)

(f) 

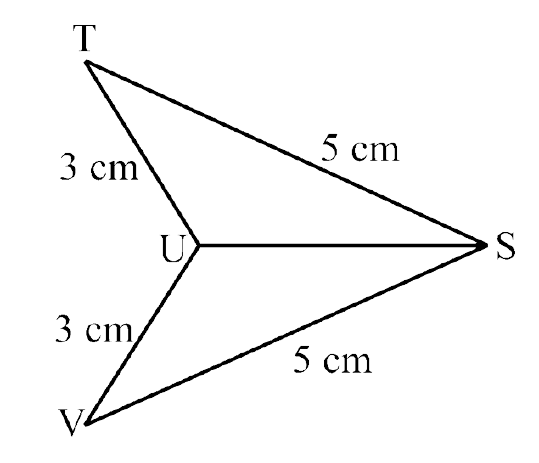
Ans: In $\triangle$STU and $\triangle$SVU,

SU = SU (common)

ST = SV = 5 cm (given)

UT = UV = 3 cm (given)

So, $\triangle$STU ≅ $\triangle$SVU (By SSS criterion)

(g) 

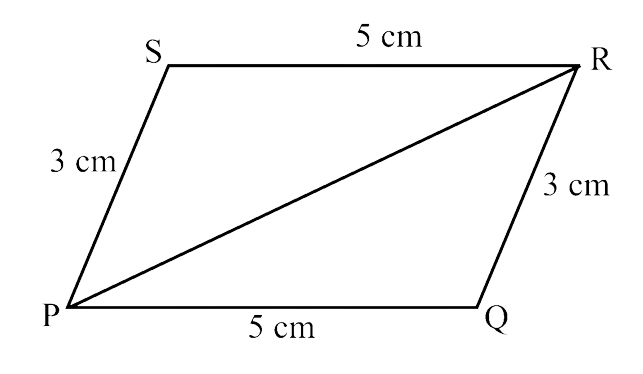
Ans: In $\triangle$PQR and $\triangle$RSP,

PR = RP (common)

PQ = RS = 5 cm (given)

OR = SP = 3 cm (given)

So, $\triangle$PQR ≅ $\triangle$RSP (By SSS criterion)

(h) 

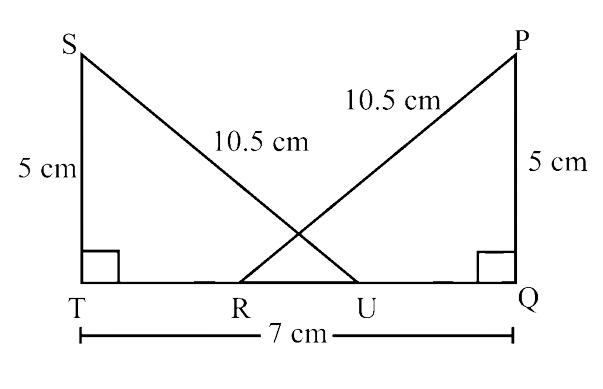
Ans: In $\triangle$STU, by Pythagoras theorem,

TU2 = (10.5)2 – 52 = 135.25

And 

In $\triangle$PQR, 

QR2 = (10.5)2 – 52 = 135.25

∴ TU2 = QR2 

$\Rightarrow$ TU = QR ……. (i)

In $\triangle$STU and $\triangle$POR,

ST = PQ = 5 cm (given)

SU = PR = 10.5 cm (given)

TU = QR (From equation (i).

So, $\triangle$STU ≅ $\triangle$PQR (By SSS criterion)

144. ABC is an isosceles triangle with AB = AC and D is the mid-point of base

BC (see figure).

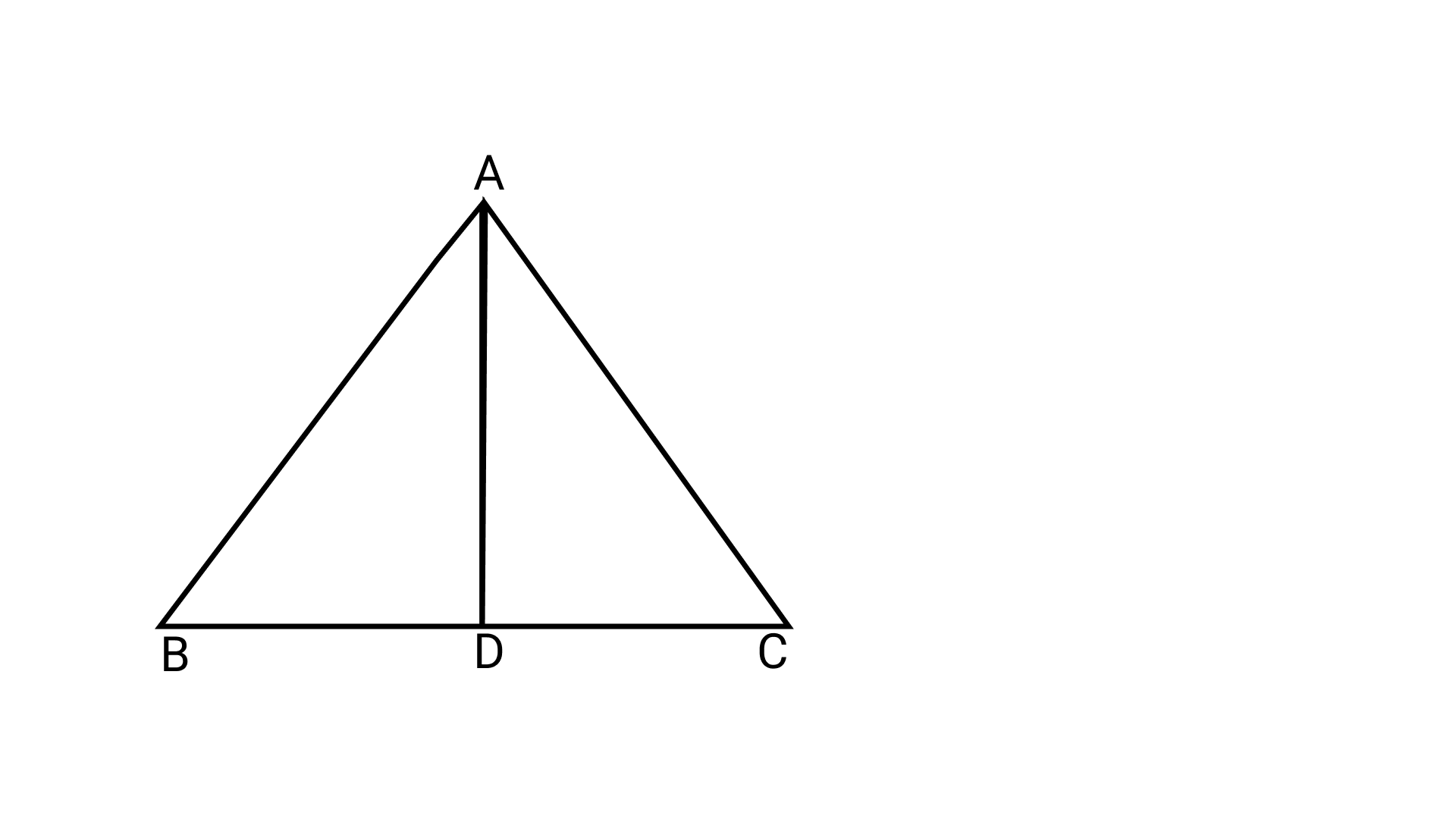
(a) State three pairs of equal parts in the triangle’s ABD and ACD. 

Ans: In $\triangle$ABD and $\triangle$ACD,

AD = AD (common)

AB = AC (given)

BD = CD (D is mid-point of BC)

(b) Is AABD AACD. If so, why? 

Ans: Yes, by using (a) part, it can be concluded that

$\triangle$ABD ≅ $\triangle$ACD (By SSS criterion)

145. In the given figure, it is given that LM = ON and NL = MO

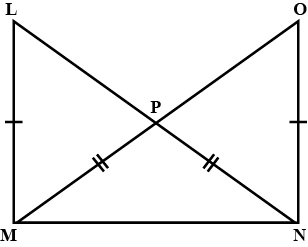
(a) State the three pairs of equal parts in the triangles NOM and MLN. 

Ans: In $\triangle$NOM and $\triangle$MLN,

NM = MN (common)

OM = LN (given)

ON = LM (given)

(b) Is $\triangle$NOM ≅ $\triangle$MLN. Give a reason. 

Ans: Yes, by using part (a), 

So, $\triangle$NOM ≅ $\triangle$MLN (By SSS criterion)

146. Triangles DEF and LMN are both isosceles with DE = DF and LM = LN,

respectively. If DE = LM and EF = MN, then, are the two triangles congruent?

Which condition do you use? If  $\angle$ E = $40^\circ$, what is the measure of  $\angle$ N?

Ans:

In $\triangle$DEF and $\triangle$LMN,

EF = MN (given)

DE = LM given

DF = LN (∵ DE = DF and LM = LN)

∴ $\triangle$DEF ≅ $\triangle$LMN (By SSS criterion)

$\Rightarrow$  $\angle$ E =  $\angle$ M (By C.P.C.T.)

Now,  $\angle$ E = $40^\circ$ 

$\Rightarrow$  $\angle$ M = $40^\circ$

Since,  $\angle$ M =  $\angle$ N (∵ LN = LM)

$\Rightarrow$  $\angle$ N = $40^\circ$

147. If APQR and ASOR are both isosceles triangle on a common base OR such

that P and S lie on the same side of QR. Are triangles PSQ and PSR congruent?

Which condition do you use?

Ans: Let $\triangle$PQR and $\triangle$SOR are the given triangles such that PQ = PR and SQ = SR.

Now, in $\triangle$PSQ and $\triangle$PSR,

PQ = PR (given)

SQ = SR (given)

PS = PS (common)

So, $\triangle$PSQ ≅ $\triangle$PSR (By SSS criterion)

Yes, the $\triangle$PSQ and $\triangle$PSR are congruent by using SSS criterion.

148. In the given figure, which pairs of triangles are congruent by SAS

congruence criterion (condition)? if congruent, write the congruence of the two

triangles in symbolic form.

(i).

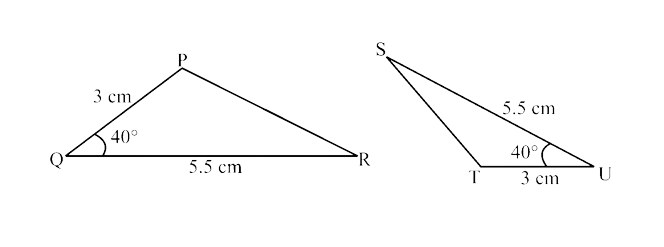
Ans: In $\triangle$POR and $\triangle$TUS,

PQ = TU = 3 cm (given)

OR = US = 5.5 cm (given)

$\angle$ POR =  $\angle$ TUS = $40^\circ$ (given)

So, $\triangle$POR ≅ $\triangle$TUS (By SAS criterion)

(ii)

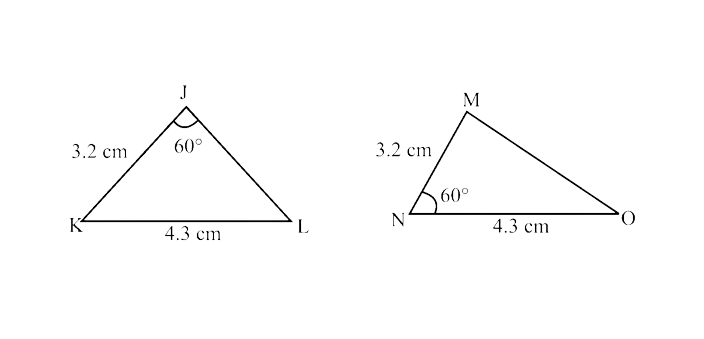
Ans: In the given figure, $\triangle$JKL and $\triangle$MNO are not congruent by any criterion.

(iii) 

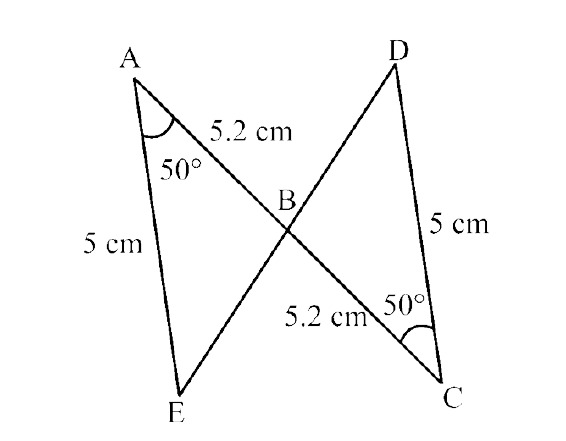
Ans: In $\triangle$ABE and $\triangle$CBD,

$\angle$ EAB =  $\angle$ DCB = $50^\circ$ (given)

AE = CD = 5 cm (given)

AB = CB = 5.2 cm (given)

So, $\triangle$ABE ≅ $\triangle$CBD (By SAS criterion)

(iv) 

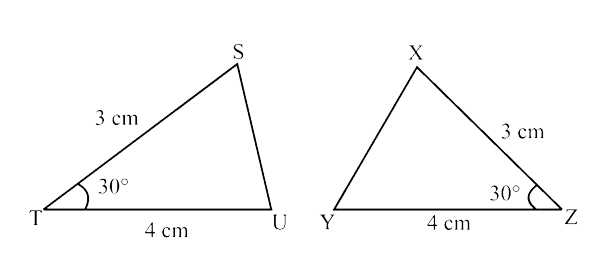
Ans: In $\triangle$SUT and $\triangle$XYZ

ST = XZ = 3 cm (given)

UT = YZ = 4 cm (given)

 $\angle$ STU =  $\angle$ XZY = $30^\circ$ (given)

So, $\triangle$SUT ≅ $\triangle$XYZ (by SAS criterion)

(v) 

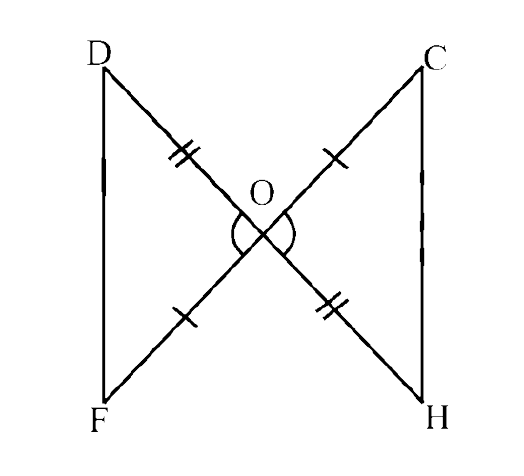
Ans: In $\triangle$DOF and $\triangle$HOC,

DO = HO (given)

FO = CO (given)

$\angle$ DOF =  $\angle$ HOC (Vertically opposite angles)

So, $\triangle$DOF ≅ AHOC (By SAS criterion)

(vi)

Ans: In $\triangle$PSQ and $\triangle$RQS.

SQ = QS (common)

PS = RQ = 4 cm (given)

$\angle$ PSQ =  $\angle$ RQS = $40^\circ$ (given)

So, $\triangle$PSQ ≅ $\triangle$ROS (By SAS criterion)

(viii) 

Ans: In $\triangle$LMN and $\triangle$OMN,

MN = MN (common)

LM = OM (given)

$\angle$ LMN =  $\angle$ OMN = $40^\circ$ (given)

So, $\triangle$LMN ≅ $\triangle$OMN (By SAS criterion)

149. State which of the following pairs of triangles are congruent. If yes, write them in symbolic form (you may draw a rough figure).

(a) $\triangle$POR : PQ = 3.5 cm, OR = 4.0 cm,  $\angle$ Q = $60^\circ$

$\triangle$ STU : ST = 3.5 cm, TU= 4 cm,  $\angle$ T = $60^\circ$

Ans: In $\triangle$PQR and $\triangle$STU,

PQ = ST = 3.5 cm (given)

$\angle$ PQR =  $\angle$ STU = $60^\circ$ (given)

OR = TU = 4 cm (given)

So, $\triangle$PQR ≅ $\triangle$STU (By SAS criterion)

(b) $\triangle$ABC : AB = 4.8 cm,  $\angle$ A = $90^\circ$, AC = 6.8 cm

$\triangle$XYZ : YZ = 6.8 cm,  $\angle$ X = $90^\circ$, ZX = 4.8 cm

Ans: Here, $\triangle$ABC and $\triangle$XYZ are not congruent by any criterion

150. In the given figure, PO = PS and  $\angle$ 1 =  $\angle$ 2.

(i) Is $\triangle$PQR = $\triangle$PSR? Give reasons.

Ans: In $\triangle$PQR and $\triangle$PSR,

PQ = PS (given)

$\angle$ 1 =  $\angle$ 2 (given)

PR = PR (common)

So, $\triangle$PQR ≅ $\triangle$PSR (By SAS criterion)

(ii) Is QR = SR? Give reasons.

Ans: Yes, QR = SR (By C.P.C.T.)

151. In the given figure, DE = IH, EG = FI and  $\angle$ E = 21. Is $\triangle$DEF ≅ $\triangle$HIG? If yes, by which congruence criterion?

Ans: EG = IF (given)

So, EG + GF = IF + GF

$\Rightarrow$ EF = IG

In $\triangle$DEF and $\triangle$HIG,

DE = HI (given)

 $\angle$ E =  $\angle$ I (given)

EF = IG 

So, $\triangle$DEF ≅ $\triangle$HIG (By SAS criterion)

152. In the given figure,  $\angle$ 1 =  $\angle$ 2 and  $\angle$ 3 =  $\angle$ 4.

(i) Is $\triangle$ADC ≅ $\triangle$ABC? Why?

Ans: In $\triangle$ADC and $\triangle$ABC

$\angle$ 1 =  $\angle$ 2 (given)

AC = AC (common)

$\angle$ 3 =  $\angle$ 4 (given)

So, $\triangle$ADC ≅ $\triangle$ABC (By ASA criterion)

(ii) Show that AD = AB and CD = CB.

Ans: By using (i) part, 

AD = AB (By C.P.C.T.)

And CD = CB (By C.P.C.T.)

153. Observe the given figure and state the three pairs of equal parts in triangles ABC and DBC.

(i) Is $\triangle$ABC = $\triangle$DCB? Why?

Ans: In $\triangle$ABC and $\triangle$DCB,

 $\angle$ ABC =  $\angle$ DCB = $40^\circ$ + $30^\circ$ = $70^\circ$ (given)

 $\angle$ ACB =  $\angle$ DBC = $30^\circ$ (given)

BC = CB (common)

So, $\triangle$ABC ≅ $\triangle$DCB (By ASA criterion)

(ii) Is AB = DC? Why?

Ans: Yes, by using (i) part, 

AB = DC (By C.P.C.T.)

(iii) Is AC = DB? Why?

Ans: Yes, by using (i) part, 

AC = DB (By C.P.C.T.)

154. In the given figure, OS ⊥ PR, RT ⊥ PQ and QS = RT.

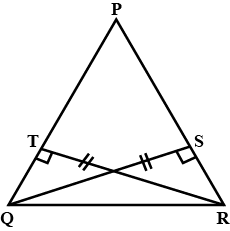
(i) Is $\triangle$QSR = $\triangle$RTQ? Give reasons.

Ans: In $\triangle$QSR and $\triangle$RTQ,

$\angle$ QSR =  $\angle$ RTQ = $90^\circ$ (As QS ⊥ PR and RT ⊥ PQ (given))

QS = RT (given)

QR = RQ (common hypotenuse)

So, $\triangle$QSR ≅ $\triangle$RTQ (By RHS criterion)

(ii) Is  $\angle$ PQR =  $\angle$ PRQ? Give reasons.

Ans: Yes, by using (i) part, 

 $\angle$ TQR =  $\angle$ SRQ (By C.P.C.T)

$\Rightarrow$  $\angle$ PQR = PRQ

155. Points A and B are on the opposite edges of a pond as shown in figure. To

find the distance between the two points, the surveyor makes a right-angled

triangle as shown. Find the distance AB.

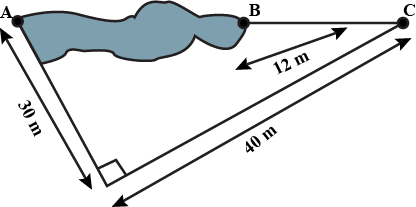
Ans: Since, $\triangle$ADC is right-angled triangle

$\therefore {\left( {AC} \right)^2}\; = {\text{ }}{\left( {AD} \right)^2}\; + {\text{ }}{\left( {CD} \right)^2} = {\text{ }}{\left( {30} \right)^2}\; + {\text{ }}{\left( {40} \right)^2}\; = {\text{ }}900{\text{ }} + {\text{ }}1600{\text{ }} = {\text{ }}2500{\text{ }} = {\text{ }}{\left( {50} \right)^2}$

$\therefore AC{\text{ }} = {\text{ }}50{\text{ m}}$ 

Now, 

AB = AC – BC = 50 – 12 = 38

Therefore, the distance AB is 38 m.

156. Two poles of 10 m and 15 m stand upright on a plane ground. If the distance between the tops is 13 m, find the distance between their feet.

Ans: Let AB and CD are the given poles of heights 15 m and 10 m such that AC =

13 m.

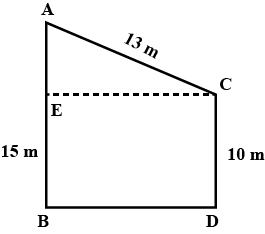
Now, BD $=\mathrm{CE}$ and $\mathrm{BE}=\mathrm{CD}=10 \mathrm{~m}$

$\therefore \mathrm{AE}=\mathrm{AB}-\mathrm{BE}=(15-10) \mathrm{m}=5 \mathrm{~m}$

Now, in $\triangle$AEC,

${\left( {AC} \right)^2}\; = {\text{ }}{\left( {AE} \right)^2}\; + {\text{ }}{\left( {EC} \right)^2}$

$\Rightarrow {\left( {13} \right)^2}\; = {\text{ }}{5^2}\; + {\text{ }}\left( {EC} \right){\;^2}$

$\Rightarrow {\left( {EC} \right)^2}\; = {\text{ }}169{\text{ }}-{\text{ }}25{\text{ }} = {\text{ }}144{\text{ }} = {\text{ }}{\left( {12} \right)^2}$

$\therefore EC{\text{ }} = {\text{ }}12{\text{ m}}$ 

Also, BD = 12 m

Thus, the distance between the feet of poles is 12 m.

157. The foot of a ladder is 6 m away from its wall and its top reaches a window

8 m above the ground,

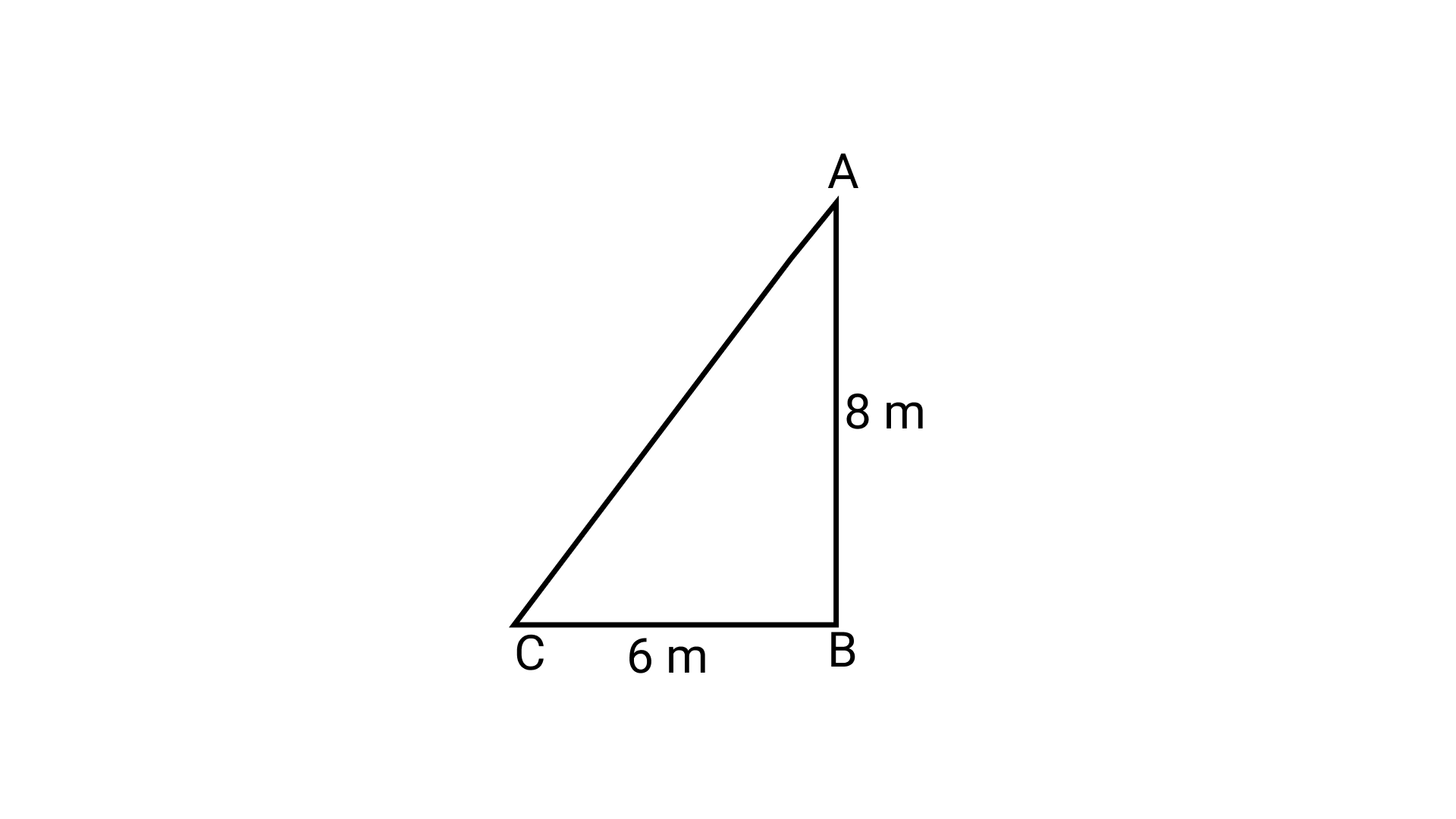
(a) Find the length of the ladder.

Ans: Let AC be the given ladder such that BC = 6 m and AB = 8 m
Now, in $\triangle \mathrm{ABC}$,

${\left( {AC} \right)^2}\; = {\text{ }}{\left( {AB} \right)^2}\; + {\text{ }}{\left( {BC} \right)^2} = {\text{ }}{8^2}\; + {\text{ }}{6^2} = {\text{ }}64{\text{ }} + {\text{ }}36{\text{ }} = {\text{ }}100{\text{ }} = {\text{ }}{\left( {10} \right)^2}$

$\therefore AC{\text{ }} = {\text{ }}10{\text{ m}}$ 

Thus, the length of the ladder is 10 m.

(b) If the ladder is shifted in such a way that its foot is 8 m away from the wall,

to what height does its top reach?

Ans: Let AC be the ladder of length 10 m and BC = 8 m.

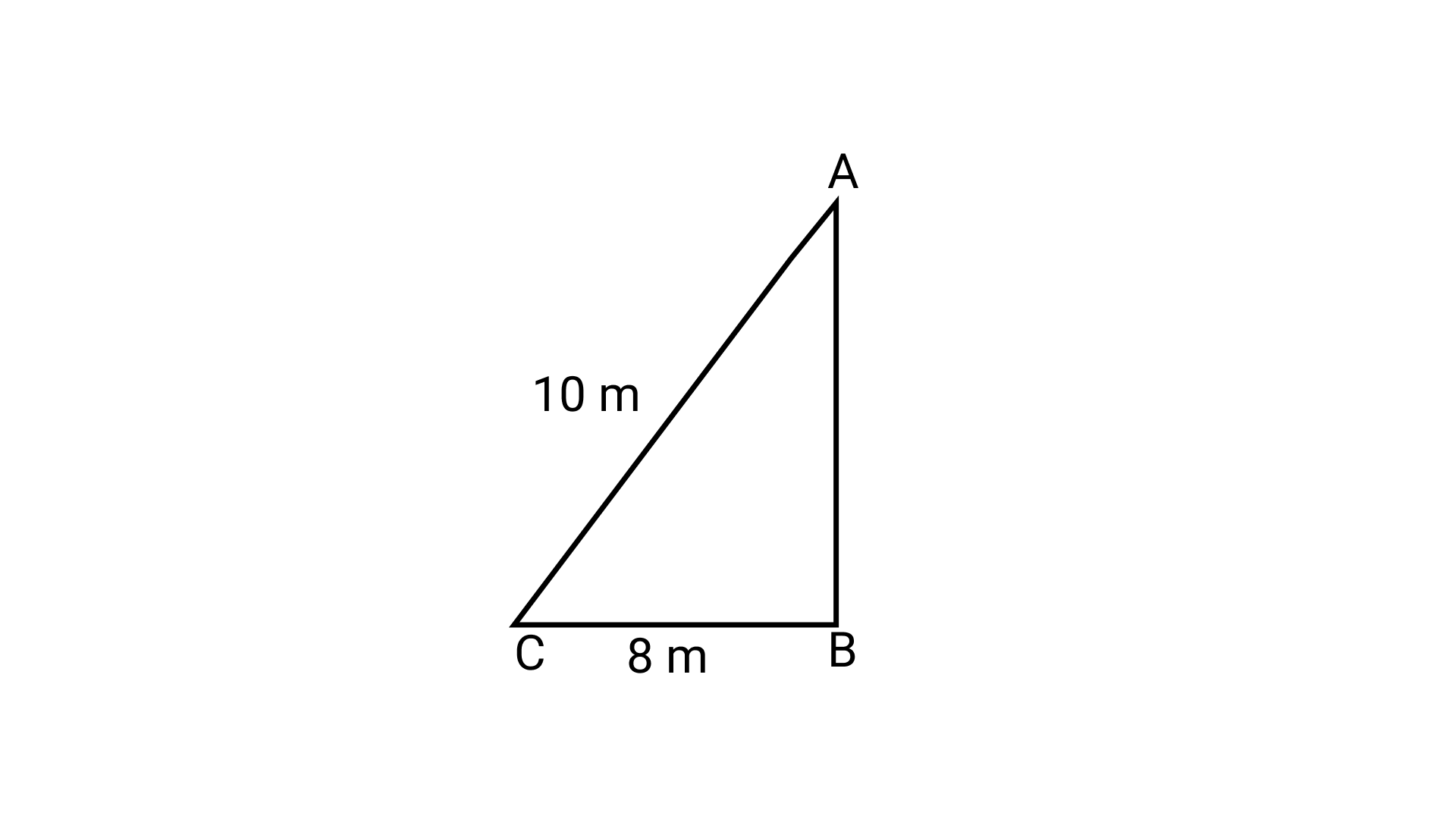
In $\triangle \mathrm{ABC}$,

${\left( {AC} \right)^2}\; = {\text{ }}{\left( {AB} \right)^2}\; + {\text{ }}{\left( {BC} \right)^2}$

$\Rightarrow {\left( {10} \right)^2}\; = {\text{ }}{\left( {AB} \right)^2}\; + {\text{ }}{\left( 8 \right)^2}$

$\Rightarrow {\left( {AB} \right)^2}\; = {\text{ }}100{\text{ }}-{\text{ }}64{\text{ }} = {\text{ }}36{\text{ }} = {\text{ }}{\left( 6 \right)^2}$

$\therefore AB{\text{ }} = {\text{ }}6{\text{ m}}$ 

Thus, the ladder top reaches 6 m above the ground.

158. In the given figure, state the three pairs of equal parts in $\triangle \mathrm{ABC}$ and $\Delta \mathbf{E O D}$.

Is $\triangle \mathrm{ABC}=\Delta \mathrm{EOD}$ ? Why?

Ans: In $\triangle \mathrm{ABC}$ and $\Delta \mathrm{EOD}$,

$\mathrm{AB}=\mathrm{EO}$ (given)

$\angle \mathrm{ABC}=\angle \mathrm{EOD}=90^{\circ}$ (given)

$\mathrm{AC}=\mathrm{ED}$ (given hypotenuse)

So, $\triangle \mathrm{ABC} \cong \triangle \mathrm{EOD}$ (By RHS criterion)

Concepts Covered in Chapter 6

• Medians of a Triangle

• Altitudes of a Triangle

• Exterior Angle of a Triangle and Its Property

• Angle Sum Property of a Triangle

• Two Special Triangles: Equilateral and Isosceles

• Sum of the Lengths of Two Sides of A Triangle

• Right-Angled Triangles and Pythagoras Property