To Find the Speed of Sound in Air at Room Temperature Using a Resonance Tube

Resonance is a special case of the forced vibration. For resonance to occur, the frequency of externally applied periodic force on the system should be equal to its natural frequency. Resonance increases the amplitude of a vibrating object. Resonance is also useful for tuning a radio receiver to the desired frequency, increasing the intensity of sound in musical instruments and analysing musical notes. We can find the speed of sound using the resonance phenomenon with the help of a resonance tube experiment.

Table of Contents:

• Aim

• Apparatus Required

• Theory

• Procedure

• Observations

• Result

• Precautions

• Lab Manual Questions

• Viva Questions

• Practical Based Questions

Aim

To find the speed of sound in air at room temperature using a resonance tube by two resonance positions

Apparatus Required

• Rubber pad

• Water in a beaker

• Resonance tube

• Set squares

• Thermometer

• Two tuning forks of known frequency

• Plumb line

Theory

We know that when a vibrating tuning fork of known frequency $\nu $ is held over the top of an air column in a glass tube, we can get a standing wave pattern in the glass tube.

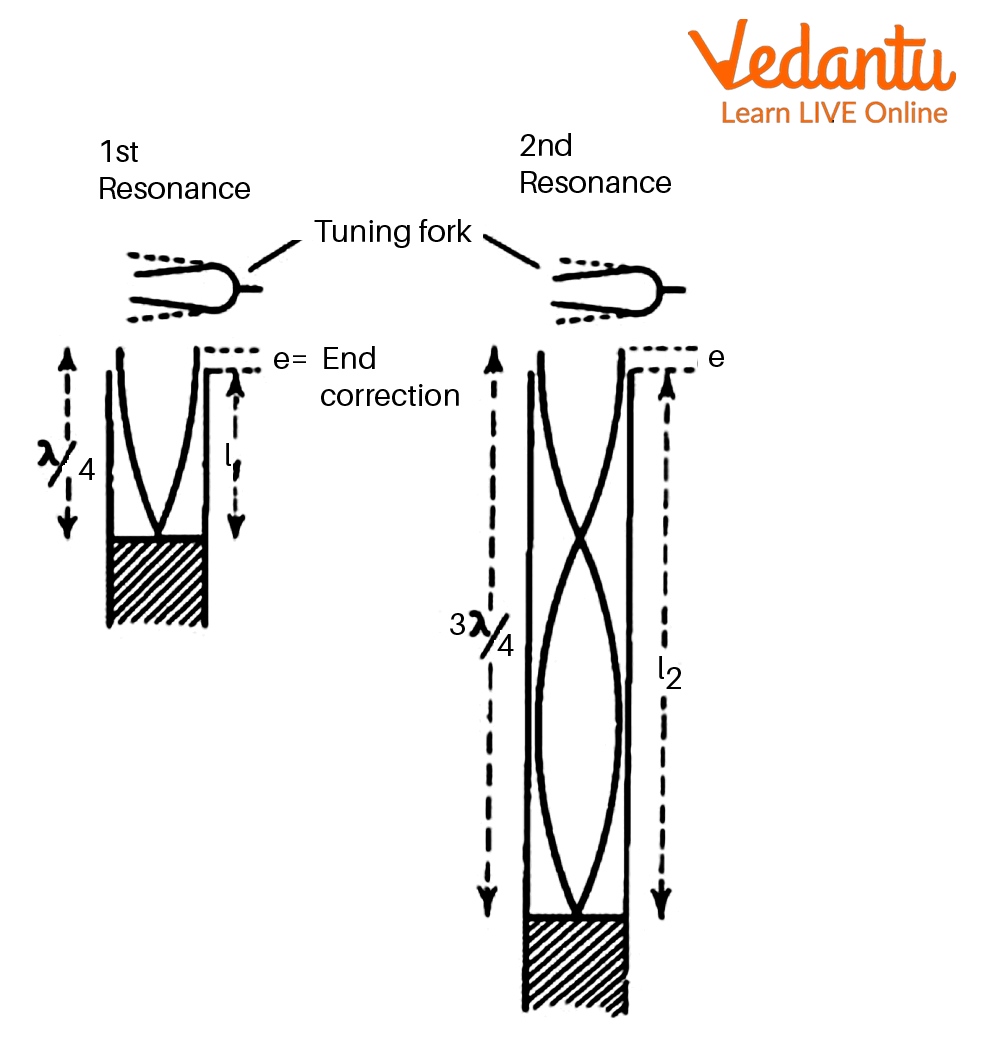
Formation of Standing Wave in Glass Tube

In a closed organ pipe like a resonance tube, there should be a zero amplitude point at the closed end. For resonance, an antinode must be formed at the open end, and a node must be formed at the closed end. Suppose the first loud sound is heard at length ${l_1}$ of the air column. When the natural frequency of the air column of length ${l_1}$ becomes equal to the natural frequency of the tuning fork, it can vibrate with the maximum amplitude. As we can see from the above figure, the length of the air column vibrating is slightly longer than the air column in the resonance tube.

For the first resonance,

$\dfrac{\lambda }{4} = {l_1} + e$

Where, $e$ is the end correction for the resonance tube, and it should be equal to $0.6r$, where $r$ = radius of the glass tube

$\lambda $ is the wavelength of the sound which is produced with the help of the tuning fork.

Now on further lowering the closed end of the tube, let the second resonance position be heard at length ${l_2}$ of the air column in the tube. This ${l_2}$ would equal approximately three-quarters of the wavelength shown in the above figure.

So, for the second resonance,

$\dfrac{{3\lambda }}{4} = {l_2} + e$

Subtract equation (ii) from equation (i),

${l_2} - {l_1} = \dfrac{\lambda }{2}$

Therefore, $\lambda  = 2\left( {{l_2} - {l_1}} \right)$

We know that velocity of sound $v = \nu \lambda $

Substituting the value of $\lambda $ in the above equation, we will get,

$v = \nu [2\left( {{l_2} - {l_1}} \right)]$

So, velocity is $v = 2\nu \left( {{l_2} - {l_1}} \right)$

Procedure

• First of all, set the resonance tube vertical by making the base horizontal, with the help of levelling screws and spirit level and note the room temperature with the help of a thermometer.

Experimental Setup

• Now, note the frequency of the given tuning fork and then fix the reservoir in the uppermost position of the vertical rod with the help of a clamp.

• Now, fill the reservoir with water with a beaker so that the tube's water level reaches its open end. Now, tighten the pinch cock and lower the position of the reservoir.

• After doing this, take a tuning fork, gently strike it on a rubber pad, and put it nearly 1 cm above the open end of the tube. 

• Now, keep both the prongs parallel to the ground so that the prongs can vibrate in the vertical plane and try to listen to the sound produced in the tube. This sound may not be audible in this position. 

• Then, slowly loosen the pinch cock so that the water level falls in the tube very slowly and keep bringing the tuning fork near the open end of the resonance tube and notice the increasing loudness of the sound.

• Repeat the above three steps till we get the exact position of the water level in the tube for which the intensity of sound becomes maximum (which is being produced in the tube). 

• If the air column length is minimum, this corresponds to the first resonance position or fundamental node. Now, we need to close the pinch cock at this position and note this position of water level or length ${l_1}$ of the air column in the tube. In this way, we can determine the first resonance position while the water level is falling in the tube.

• Repeat the above steps to confirm the first resonance position. 

• Then, find out the first resonance position by gradually raising the level of water in the tube and holding the vibrating tuning fork continuously on the top of its open end and fix the tube at the position where the sound of maximum intensity is heard.

• Now, to determine the second resonance position, lower the position of the water level further in the resonance tube by sliding down the position of the reservoir on the vertical stand and opening the pinch cock till the length of the air column in the tube increases about three times of the length ${l_1}$

• Now, find out the second resonance position and determine the length of air column ${l_2}$ in the resonance tube with the same tuning fork having frequency ${\nu _1}$ and confirm the length ${l_2}$ by taking four readings, two when the level of water is falling and the other two when the level of water is rising in the resonance tube. 

• Repeat the above steps with a second tuning fork having frequency ${\nu _2}$ and determine the first and second resonance positions, and we should calculate the sound velocity in each case. 

Observations

• Temperature of the room $\theta $ = _____ $^\circ C$

• Frequency of first tuning fork ${\nu _1}$ = _____ $Hz$

• Frequency of second tuning fork ${\nu _2}$ = _____ $Hz$

• Frequency of first tuning fork is ${\nu _1}$ = _____ $Hz$ 

• Velocity of sound in air can be calculated as ${v_1} = 2{\nu _1}\left( {{l_2} - {l_1}} \right)$ = _____ $m{s^{ - 1}}$ 

• Frequency for second tuning fork is ${\nu _2}$ = _____ $Hz$

• So, velocity of sound in air can be calculated as, ${v_2} = 2{\nu _2}\left( {{l_2} - {l_1}} \right)$ = _____ $m{s^{ - 1}}$ 

So, the mean velocity of sound $v$ in air at room temperature can be calculated by, 

$v = \dfrac{{{v_1} + {v_2}}}{2}$ $m{s^{ - 1}}$ 

Result

The velocity of sound in air (at room temperature) is $v = \dfrac{{{v_1} + {v_2}}}{2}$ = _____ $m{s^{ - 1}}$ 

Precautions

• We should keep the resonance tube vertical using the levelling screws.

• To identify the resonance positions properly, we should perform this experiment in a quiet atmosphere.

• Resonance tube which we are using to perform this experiment must be of a uniform area of cross-section. 

Lab Manual Questions 

1. What have forced vibrations?

Ans: When an object is made to vibrate with an external periodic force different from the object's natural frequency, then that object's vibrations are called forced vibrations.

2. Write one possible error that can affect the result of this experiment.

Ans: The humidity above the enclosed water column can increase sound velocity. This is the possible error that can affect the final result of this experiment. 

3. What is a tuning fork? 

Ans: A tuning fork is the simplest source of the sound. It consists of a U-shaped bar of metal with arms of exactly equal length and mass and with a stem provided in the middle. It freely vibrates on its resonance frequency.

4. What is the resonance tube's operating principle?

Ans: The resonance of an air column with a tuning fork is the basis for the resonance tube. In the air column, stationary transverse waves form. The wave's node is at the water's surface, and its antinode is at the open end of the tube.

Viva Questions

1. On what principle does the resonance tube work?

Ans: The resonance tube works on the principle of the air column with a tuning fork.

2. Is there a node or antinode at the open end of the water level in this experiment?

Ans: It is an antinode at the open end of the water level in this experiment.

3. Do we find the velocity of sound in the air column or the water column?

Ans: We find the sound velocity in the air column above the water column.

4. On what principle does the guitar work?

Ans: Guitar works on the principle of resonance of sound.

5. What type of waves can we produce in the air column?

Ans: We can produce longitudinal stationary waves in the air column. 

6. Will we get different results if we take liquids other than water?

Ans: We will get the same result if we take liquids other than water.

7. What is the meaning of the frequency of the tuning fork?

Ans: The number of vibrations completed by a prong of the tuning fork per second is called the frequency of the tuning fork.

8. Is there a node or antinode at the close end of the water level in this experiment? 

Ans: It is a node at the open end of the water level in this experiment.

Practical Based Questions

1. What happens to the resonance position if we use kerosene oil in place of water in this experiment?

1. Increases

2. Decreases

3. Remains unchanged

4. Becomes almost zero

Ans: Option C - Remains unchanged 

2. The velocity of sound in air (at room temperature) is directly proportional to the _____

1. Wavelength of light

2. Square root of temperature (in Kelvin)

3. Intensity of magnetic field

4. Frequency of light

Ans: Option B - Square root of temperature (in Kelvin)

3. We can produce sound with the help of _____ object.

1. Still

2. Stationary

3. Moving

4. Vibrating

Ans: Option D - Vibrating

4. In which of the following medium speed of sound would be maximum?

1. Oil

2. Wind

3. Steel

4. None of the above

Ans: Option C - Steel

5. Sound travels slowest in _____

1. Liquids

2. Solids 

3. Gases

4. None of the above

Ans: Option C - Gases

6. The speed of sound in distilled water is _____ the speed of sound in oxygen.

1. Greater than

2. Same as

3. Less than

4. None of the above

Ans: Option A - Greater than

7. Sound waves can not pass through _____

1. Water

2. Air

3. Vacuum

4. Solid

Ans: Option C - Vacuum

8. We can measure speed of sound in _____

1. Metre/second

2. Ohm

3. Tesla

4. Newton

Ans: Option A - Metre/second

9. Sound waves are _____

1. Non-mechanical waves

2. Transverse waves

3. Longitudinal mechanical waves

4. Both A and B

Ans: Option C - Longitudinal mechanical waves

10. SI unit of frequency is

1. Kelvin

2. Newton

3. Tesla

4. Hertz

Ans: Option D - Hertz

Conclusion

This experiment was developed to investigate the standing waves in a closed pipe and to determine the speed of sound in air at room temperature. We can conclude from this experiment that

• The difference between the theoretical and experimental value of the speed of sound in air at room temperature is very small. 

• End correction does not affect the final result of this experiment.