Physics Experiment- To Prove Triangle Law of Vector Addition - Introduction
Any quantity with both magnitude and direction is referred to as a vector. Examples of vector quantities are displacement, acceleration, force, momentum, pressure etc.
The process of adding two or more vectors is known as vector addition. From the geometrical method of addition of vectors, vector laws of addition can be divided into two categories: The triangle law of vector addition and the parallelogram law of vector addition.
To understand the combined effect of different vector quantities, the law of vector addition is very much useful and applied in a combined work force, like pulling/pushing the heavier objects, operation of ships during the heavy wind, etc.
Table of Content
Aim
Theory
Apparatus Required
Procedure
Observations
Result
Precautions
Aim
To prove the Triangle law of vector addition.
Theory
Based on the arrangement of vectors (say P and Q), heads and tails, the laws of vector addition are determined.
The triangle law of vector addition is applied when two vectors are positioned head to tail.
The parallelogram law of vector addition is applied whenever two vectors are arranged head to head or tail to tail.
Statement of Triangular Law of Vector Addition
"When two sides of a triangle represent two vectors, and those sides are taken in the same order in terms of magnitude and direction, the third side of that triangle represents the vector’s resultant in terms of magnitude and direction (see figure below)."
Let's assume two vectors, vector P and vector Q, as defined in figure (a) below. Now, connect the head of vector P to the tail of vector Q. In this case, the vectors' directions are unchanged, as shown in figure (b) below. Draw a straight line at an angle with respect to the vector P connecting the head of vector P to the tail of vector Q [as shown in figure (c) below]. Now, the resulting vector, vector R, is the resultant vector after the addition of the vectors P and Q.
\[\mathop P\limits^ \to + \mathop Q\limits^ \to = \mathop R\limits^ \to \]
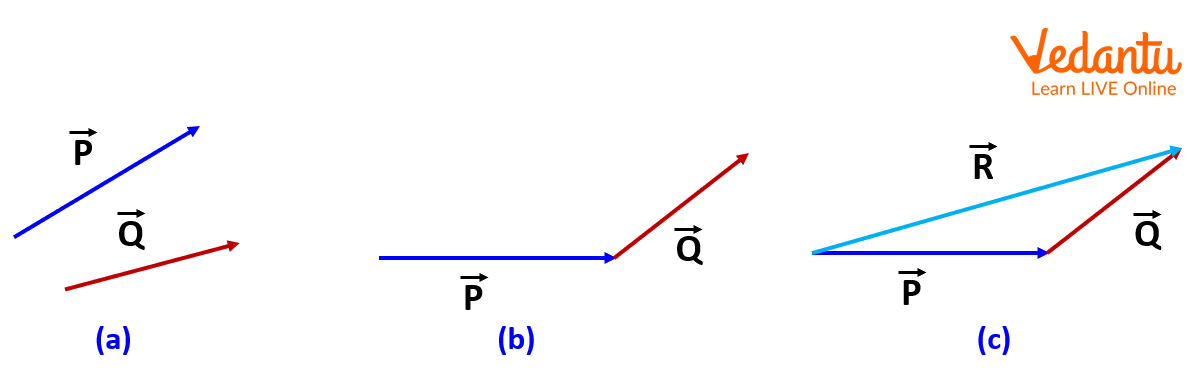
Description of the Triangle Law of Vector Addition
Apparatus Required
Three hangers
A known object whose mass needs to be calculated
Thin rope
White sheets of paper
A strip of mirrors
Protector
Thumb pins
Scale of one-half meter
A spring balances
Procedure
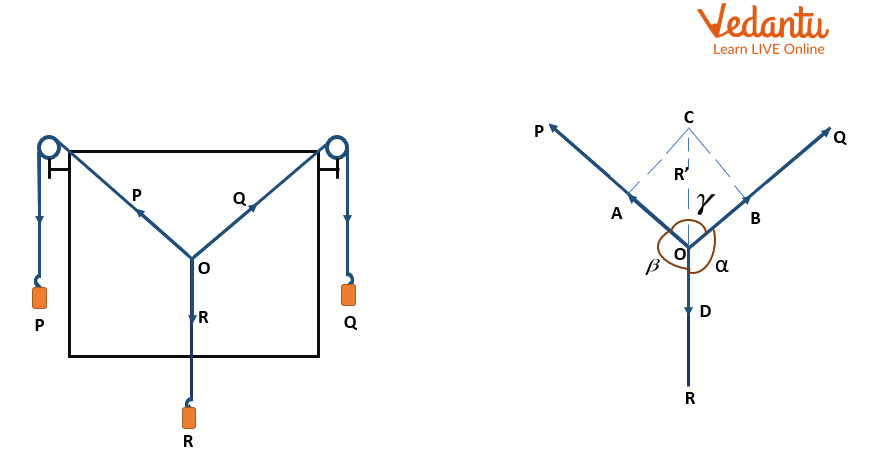
Experimental Arrangement of Triangular Law of Vector Addition
A drawing board is kept vertically on a wall using two small, smooth pulleys fixed to each of the upper corners, as shown in above figure.
There should be no resistance when the pulleys move. Both pulleys are made to pass under a thin thread.
The two free ends of the string are connected to two slotted weights P and Q, each of which weighs 50 g.
At O, a second short thread is knotted to the first string's centre. On the free end of the short string is a third slotted weight R. The system is set to rest by adjusting the weights P, Q, and R.
Under the influence of the three forces P, Q, and R operating along the strings, the point O is in equilibrium.
A white piece of paper is now held just behind the thread, keeping it away from them.
The three forces P, Q, and R are represented in magnitude by the common knot O and the directions OA, OB, and OD on any practical scale (such as 50 g = 1 cm).
Observations
The resultant of forces P (OA = BC) and Q (OB = AC) is represented in magnitude and direction by OC, which is taken in the opposite direction, according to the triangle law of forces.
In order to verify the triangle law of vector addition the ratios \[\dfrac{P}{{OA}}\], \[\dfrac{Q}{{OB}}\] and \[\dfrac{R}{{OC}}\] are computed and tabulated (see below Table).
The triangle law of forces will be demonstrated by the fact that all of the three ratios defined above are equal.
Observation Table
Result
Ratios \[\dfrac{P}{{OA}}\], \[\dfrac{Q}{{OB}}\] and \[\dfrac{R}{{OC}}\] are equal or not. Write your observations.
Precautions
There should be no resistance when the pulley is being pulled.
The drawing board should be kept vertically.
Please keep all the strings strained.
Test the spring balances prior to their functioning.
Lab Manual Questions
1. State triangular law of vector addition.
Ans: When the two sides of a triangle represent the two vectors in terms of magnitude and direction, the third side of that triangle represents the vectors' resultant in magnitude and direction.
2. From the experiment performed above, why is vector addition essential to physics?
Ans: There are several vector quantities in physics. Vector addition is used to determine their combined effect on the item when they are acting simultaneously on a body.
3. When the three forces act on an object to bring equilibrium, what is the product of the first two forces?
Ans: The first two forces must be equal and opposing to the third force.
4. Is there any force on the pulleys when the knot is at equilibrium?
Ans: The net force acting on the knot must be zero to be in equilibrium. As a result, both the horizontal and vertical components must be zero (within the margin of experimental error).
Viva Questions
1. When should we apply the triangular law of vector addition?
Ans: When two vectors are oriented head to tail, the triangle law of vector addition is used to add the two vectors. The resultant vector is calculated using the triangle law of vector addition.
2. What are the two laws for vector additions?
Ans: two types of vector additions are as follows:
Triangular law of vector addition
Parallelogram law of vector addition
3. When should we apply the parallelogram law of vector addition?
Ans: When either the head or the tail of two vectors are connected to a common point, the parallelogram law of vector addition is employed to add the two vectors. The resultant vector is computed using the parallelogram law of vector addition.
4. What does the resultant vector in the parallelogram law of vector addition represent?
Ans: The resultant vector is represented by the diagonal in the parallelogram law of vector addition.
5. Calculate the magnitude of the given vector.
\[\mathop a\limits^ \to = 3\hat i - 6\hat j + 5\hat k\]
Ans: Given, \[\mathop a\limits^ \to = 3\hat i - 6\hat j + 5\hat k\]
x=3, y=-6 and z=5
For Vector A,
\[\begin{array}{l}\left| A \right| = \sqrt {{x^2} + {y^2} + {z^2}} \\\left| A \right| = \sqrt {{3^2} + {{( - 6)}^2} + {5^2}} \\\left| A \right| = \sqrt {70} \\\left| A \right| = 8.36\end{array}\]
Therefore, the magnitude of vector A is 8.36
6. Determine the magnitude of the vector: \[2\hat i - 3\hat j + 4\hat k\]
Ans: Let the vector magnitude be A
So \[A = 2\hat i - 3\hat j + 4\hat k\]
Here, x= 2, y= -3 and z=4
Therefore,
\[\begin{array}{l}\left| A \right| = \sqrt {{x^2} + {y^2} + {z^2}} \\\left| A \right| = \sqrt {{2^2} + {{( - 3)}^2} + {4^2}} \\\left| A \right| = \sqrt {29} \\\end{array}\]
The magnitude of vector A = \[\sqrt {29} \]
7. Calculate the magnitude of a vector \[Q = \hat i - 3\hat j - 4\hat k\]
Ans: Here, x=1, y=-3 and z=-4
\[\begin{array}{l}\left| A \right| = \sqrt {{x^2} + {y^2} + {z^2}} \\\left| A \right| = \sqrt {{1^2} + {{( - 3)}^2} + {{( - 4)}^2}} \\\left| A \right| = \sqrt {26} \\\end{array}\]
The magnitude of the vector Q=\[\sqrt {26} \]
8. What will be the unknown vector, if the resultant vector is \[25\hat i - 10\hat j\] and the vector added to the other vector is \[10\hat i - 5\hat j\]?
Ans: let the resultant vector be R and the other two vectors be P and Q
So, \[R = 25\hat i - 10\hat j\] and taken P as the known vector, \[P = 10\hat i - 5\hat j\]
So The unknown vector Q be
\[\begin{array}{l}Q = R - P\\Q = 25\hat i - 10\hat j - (10\hat i - 5\hat j)\\Q = 15\hat i - 5\hat j\end{array}\]
So the unknown vector is \[Q = 15\hat i - 5\hat j\]
9. What will be the unknown vector, if the resultant vector is \[3\hat i - 7\hat j\] and the vector added to the other vector is \[10\hat i - 5\hat j\]?
Ans: Let the resultant vector be R and the other two vectors be P and Q
So\[R = 3\hat i - 7\hat j\] and taken P as the known vector, \[P = 10\hat i - 5\hat j\]
So, the unknown vector Q be
\[\begin{array}{l}Q = R - P\\Q = 3\hat i - 7\hat j - (10\hat i - 5\hat j)\\Q = - 7\hat i - 2\hat j\end{array}\]
So, the unknown vector is \[Q = - 7\hat i - 2\hat j\]
10. Adding \[A = 36\hat i - 47\hat j\] and \[B = 16\hat i - 12\hat j\] gives?
Ans: \[\begin{array}{l}A + B = 36\hat i - 47\hat j + (16\hat i - 12\hat j)\\A + B = 52\hat i - 35\hat j\end{array}\]
Ans: ${A + B = 36\hat i - 47\hat j + (16\hat i - 12\hat j)}$
${A + B = 52\hat i - 35\hat j}$
Practical-Based Questions
1. Two magnets P and Q are attracted by the same metal ball. The force by which the ball gets attracted by the magnet is taken as \[\mathop p\limits^ \to \] and\[\mathop q\limits^ \to \]. Which option describes the exact meaning of the statement?
\[\mathop p\limits^ \to \ne \mathop q\limits^ \to \]
Both the magnets don’t pull the ball with the same strength and in the same direction
Both the magnets pull the ball with the same strength but in different direction
Either the magnets don’t pull with the same strength or they don’t pull in the same direction
None of the above
Ans: C) either the magnets don’t pull either the same strength or they don’t pull in the same direction
2. Which vector formula is being used to determine relative velocity?
Vector subtraction
Vector multiplication
Vector addition
Vector division
Ans: A) Vector subtraction
3. Which option from the following is incorrect?
Cross product is distributive over addition
Dot product is commutative
Cross product is commutative
None of the above
Ans: C) Cross product is commutative
4. What will be the magnitude of the resultant vector if the two vectors are moving in the same direction
Product of the vector’s magnitude
Difference between the magnitude of vectors
Sum of the roots of the vectors
Sum of the magnitude of the vectors
Ans: C) Sum of the magnitude of the vectors
5. What do we get when we add up two vectors?
An operation
A vector
A number
A scalar quantity
Ans: B) A vector
6. What do you mean by a scalar quantity?
A quantity with both direction and magnitude
A quantity having direction only
A quantity having magnitude only
None of the above
Ans: C) A quantity having magnitude only
7. What is the term given to the vector which is being obtained by the addition of two vectors?
Sum vector
New vector
Derived vector
Resultant vector
Ans: D) Resultant vector
8. The operation that does not result in a vector from the input of two vectors is
Vector addition,
Vector subtraction,
Dot product,
Cross product
Ans: A) Vector Addition
9. Can a scalar quantity be added to a vector quantity?
Yes
No
Maybe
Ans: No) A vector quantity can be added to a vector, and a scalar quantity can be only added to a scalar.
10. Which option from the following is incorrect
Vector can be multiplied by scalar
Vector quantity which is being added to a scalar quantity
Vector quantity which is being subtracted from a scalar quantity
None of the above
Ans: A) Vector can be multiplied by scalar
Conclusion
From this article we can understand that to calculate the sum of two vectors, one can apply the triangular law of vector addition. From this experiment, the students can obtain the resultant vector from the experiment using a graph and then calculate it theoretically and then compare both results. Hence, by reading this article, students can understand the triangular law of vector addition theoretically as well as experimentally.
FAQs on CBSE Physics Experiment To Prove Triangle Law of Vector Addition
1. Calculate the angle between the two vectors from the given equations.
\[\begin{array}{l}2\hat i - \hat j + 3\hat k\\3\hat i - \hat j + \hat k\end{array}\]
Let,
\[\begin{array}{l}\vec a = 2\hat i - \hat j + 3\hat k\\\vec b = 3\hat i - \hat j + \hat k\end{array}\]
And we know that,\[\vec a.\vec b = \left| a \right|.\left| b \right|.\cos \theta \]
So,
\[\begin{array}{l}\vec a.\vec b = (2\hat i - \hat j + 3\hat k).(3\hat i - \hat j + \hat k)\\\vec a.\vec b = (2).(3) + ( - 1).( - 1) + (3).(1)\\\vec a.\vec b = 6 + 1 + 3\\\vec a.\vec b = 10\end{array}\]
Magnitude of A will be,
\[\begin{array}{l}\left| a \right| = \sqrt {{2^2} + {{( - 1)}^2} + {3^2}} \\\left| a \right| = \sqrt {4 + 1 + 9} \\\left| a \right| = \sqrt {14} \end{array}\]
Magnitude of B will be,
\[\begin{array}{l}\left| b \right| = \sqrt {{3^2} + {{( - 1)}^2} + {1^2}} \\\left| b \right| = \sqrt {9 + 1 + 1} \\\left| b \right| = \sqrt {11} \end{array}\]
From, \[\vec a.\vec b = \left| a \right|.\left| b \right|.\cos \theta \], we get,
\[\begin{array}{l}\vec a.\vec b = \left| a \right|.\left| b \right|.\cos \theta \\10 = \sqrt {14} \times \sqrt {11} \times \cos \theta \\10 = \sqrt {154} \cos \theta \\\cos \theta = \dfrac{{10}}{{\sqrt {154} }}\\\theta = {\cos ^{ - 1}}\dfrac{{10}}{{\sqrt {154} }}\end{array}\]
2. Calculate the angle between the two vectors from the given equation.
\[\begin{array}{l}\vec a = \hat i - \hat j + 3\hat k\\\vec b = 4\hat i - \hat j + \hat k\end{array}\]
Given,
\[\begin{array}{l}\vec a = \hat i - \hat j + 3\hat k\\\vec b = 4\hat i - \hat j + \hat k\end{array}\]
And we know that \[\vec a.\vec b = \left| a \right|.\left| b \right|.\cos \theta \]
And,
\[\begin{array}{l}\vec a.\vec b = (\hat i - \hat j + 3\hat k).(4\hat i - \hat j + \hat k)\\\vec a.\vec b = (1).(4) + ( - 1).( - 1) + (3).(1)\\\vec a.\vec b = 4 + 1 + 3\\\vec a.\vec b = 8\end{array}\]
Magnitude of A and B are:
\[\begin{array}{l}\left| a \right| = \sqrt {{1^2} + {{( - 1)}^2} + {3^2}} \\\left| a \right| = \sqrt {1 + 1 + 9} \\\left| a \right| = \sqrt {11} \end{array}\]
\[\begin{array}{l}\left| b \right| = \sqrt {{4^2} + {{( - 1)}^2} + {1^2}} \\\left| b \right| = \sqrt {16 + 1 + 1} \\\left| b \right| = \sqrt {18} \end{array}\]
Now from \[\vec a.\vec b = \left| a \right|.\left| b \right|.\cos \theta \]we get,
\[\begin{array}{l}\vec a.\vec b = \left| a \right|.\left| b \right|.\cos \theta \\8 = \sqrt {11} \times \sqrt {18} \times \cos \theta \\8 = \sqrt {198} \cos \theta \\\cos \theta = \dfrac{{18}}{{\sqrt {198} }}\\\theta = {\cos ^{ - 1}}\dfrac{8}{{\sqrt {198} }}\end{array}\]
3. Find the unit vector in the direction of the vector from the given equation.
\[\vec a = 2\hat i + 3\hat j + 3\hat k\]
Given vector,\[\vec a = 2\hat i + 3\hat j + 3\hat k\],
To find the magnitude of vector:
\[\begin{array}{l}\left| a \right| = \sqrt {{2^2} + {3^2} + {3^2}} \\\left| a \right| = \sqrt {4 + 9 + 9} \\\left| a \right| = \sqrt {22} \end{array}\]
Substituting the values, we get
\[\begin{array}{l}\hat a = \dfrac{1}{{\sqrt {22} }}(2\hat i + 3\hat j + 3\hat k)\\\hat a = \dfrac{{2\hat i}}{{\sqrt {22} }} + \dfrac{{3\hat j}}{{\sqrt {22} }} + \dfrac{{3\hat k}}{{\sqrt {22} }}\end{array}\]
4. What purpose do vectors serve in Physics?
Physics heavily relies on vectors. Vectors can depict a body's forces, acceleration, and velocity. Many additional physical values can be regarded as vectors. The direction of an arrow and length can still be used to denote their directions and magnitude, even when most do not indicate distance. The coordinate system used to describe physical vectors affects how they are mathematically described.
