Question

A block of mass 5 kg is on a rough horizontal surface and is at rest. Now a force of 24 N is imparted to it with negligible impulse. If the coefficient of kinetic friction is 0.4 and \[g{\text{ }} = {\text{ }}9.8\;m/{s^2}\], then the acceleration of the block is

Answer 1

Hint:
The coefficient of kinetic friction is a measure of how much resistance there is to sliding motion between two surfaces. The coefficient of kinetic friction is always less than or equal to the coefficient of static friction. Make a free body diagram of the body. Frictional force is given by $f = \mu N$ where N is the normal force and $\mu $coefficient of kinetic friction.




Complete step by step solution:

First see a picture of the scenario. Let's draw a free body diagram.

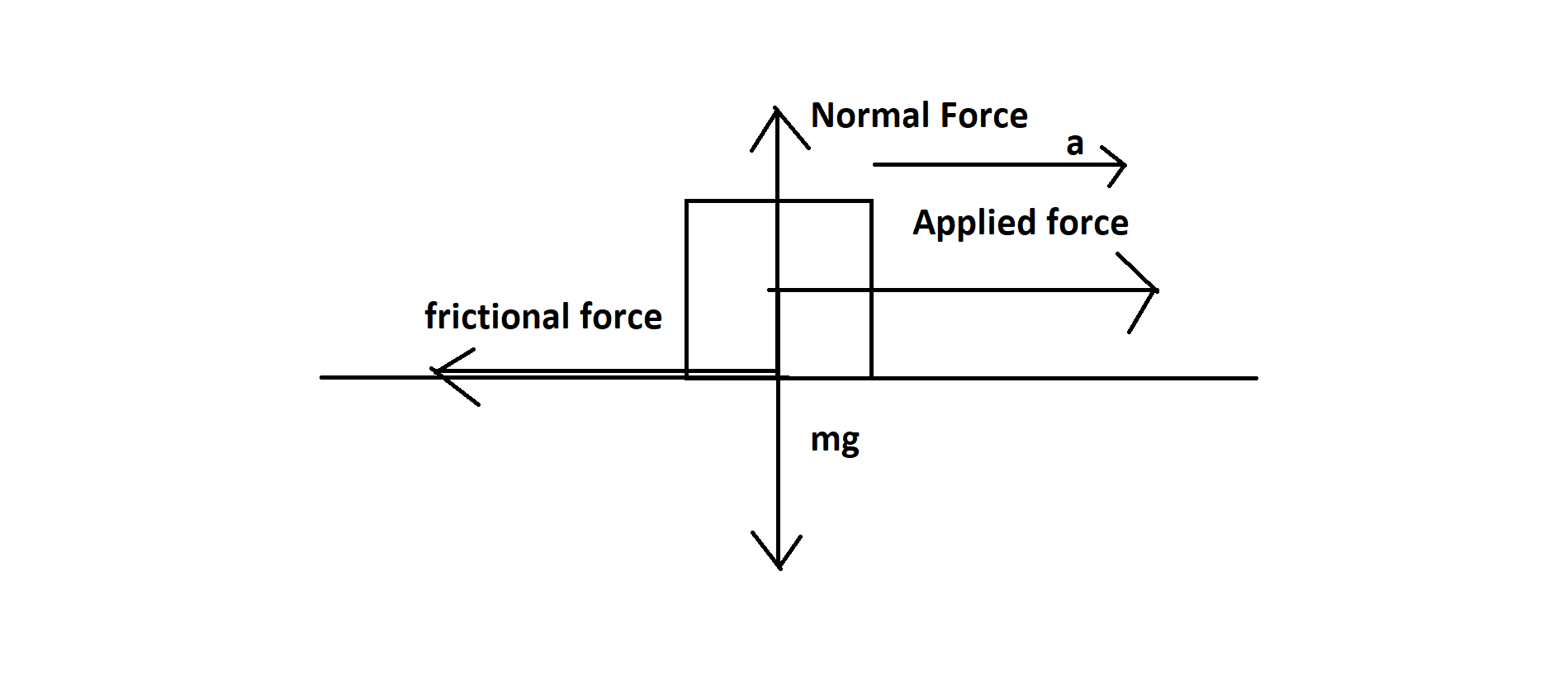
Here we are considering a body of mass m moving with an acceleration and frictional force opposing its motion. friction is a force that resists the sliding of two surfaces against each other. The frictional force is proportional to the normal force, which is the force that is perpendicular to the surfaces. The coefficient of friction, $\mu $, determines how much friction there is between the two surfaces. We can define friction as $f = \mu N$ where N is the normal. Normal force is the force exerted by a surface on an object in contact with it. This force is perpendicular to the surface and is responsible for keeping objects in contact with each other. Here we see that normal force is balanced by the weight of the body. That means $N = mg$ . so, we can also write $f = \mu mg$ . Now we can write the equation as $F - \mu mg = ma$ Here F is applied force. Now let’s put the values on the equation.
$F - \mu mg = ma$
$\begin{gathered}
  {\text{or, }}24 - 0.4 \times 5 \times 9.8 = 5a \\
  or,4.4 \div 5 = a \\
\end{gathered} $
$or,a = 0.88m{s^{ - 2}}$
Acceleration of the body is $0.88m{s^{ - 2}}$.



Note:
A force called friction prevents two surfaces from sliding against one another. The normal force, or the force that is perpendicular to the surfaces, is directly proportional to the frictional force and mathematically given by $f = \mu N$.