




Step-by-Step Solution: How to Find Nth Roots of Unity
De Moivre’s Theorem and the concept of nth roots of unity form the backbone of several analytical results in complex numbers and trigonometry. Mastery of these topics is essential for excelling in advanced mathematics, including applications in number theory and engineering. Both topics are also crucial for understanding various problems in the JEE Main examination.
Complex Numbers in Polar Form
A complex number $z = x + iy$ can be represented in polar form as $z = r(\cos \theta + i\sin \theta)$, where $r = |z| = \sqrt{x^2 + y^2}$ and $\theta = \arg(z)$ is the argument, or angle, formed with the positive real axis.
This representation is fundamental for subsequent analysis, since De Moivre’s Theorem relates directly to powers and roots of complex numbers in polar form. For further review, refer to Complex Numbers Overview.
De Moivre’s Theorem: Statement and Proof
De Moivre’s Theorem establishes a direct method to raise complex numbers in polar form to integer powers. The theorem states that for any real $\theta$ and integer $n$,
$\bigl( \cos \theta + i\sin \theta \bigr)^n = \cos(n\theta) + i\sin(n\theta)$
This concise result provides a bridge between powers of complex numbers and trigonometric multiple-angle identities.
To prove De Moivre’s Theorem for positive integers, expand $(\cos \theta + i\sin \theta)^n$ using the binomial theorem, expressing all terms in powers of $i$. By collecting real and imaginary parts and employing the Euler formula $e^{i\theta} = \cos \theta + i\sin \theta$, the right side is obtained. For negative $n$, the result follows by using the reciprocal and the identities $\cos(-\theta) = \cos \theta$, $\sin(-\theta) = -\sin \theta$.
Applications of De Moivre’s Theorem
De Moivre's Theorem streamlines the computation of powers of complex numbers. It is also commonly applied to derive trigonometric identities for $\cos n\theta$ and $\sin n\theta$ in terms of $\cos \theta$ and $\sin \theta$.
By expanding both sides and equating real and imaginary parts, one obtains readily usable expressions for multiple-angle formulas. These results are instrumental in several branches of mathematics and in solving problems with roots of unity.
Definition of nth Roots of Unity
An nth root of unity is a complex number $z$ satisfying the equation $z^n = 1$, where $n$ is a positive integer. These solutions are precisely the values which, when raised to the $n$th power, yield unity.
Expressing unity in polar form as $1 = \cos 0 + i\sin 0 = e^{i \cdot 0}$, the general solution to $z^n=1$ can be written using De Moivre’s Theorem:
$z_k = \cos\left( \dfrac{2\pi k}{n} \right) + i \sin\left( \dfrac{2\pi k}{n} \right) = e^{\frac{2\pi i k}{n}}$, where $k = 0, 1, 2, \dots, n-1$.
Pictorial Representation and Geometric Structure
The set of all nth roots of unity forms a regular $n$-gon on the complex plane, inscribed in the unit circle, centered at the origin. Each root corresponds to an angle increment of $\frac{2\pi}{n}$ radians from $1$ along the circle.
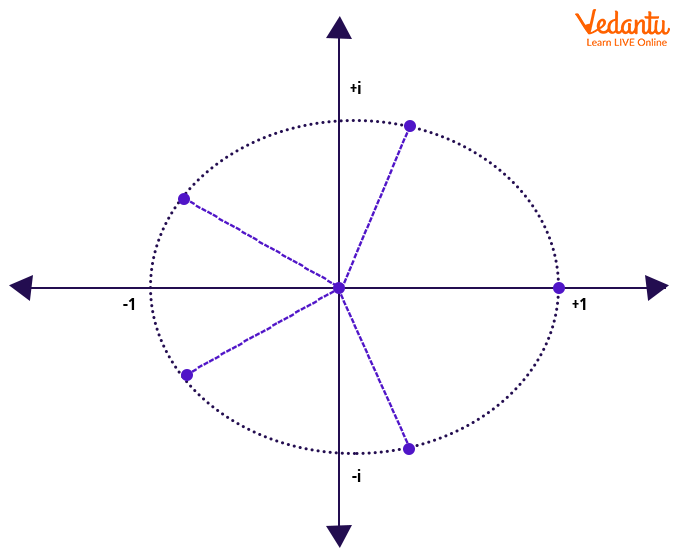
These points are equally spaced, and their symmetric arrangement underlies many important algebraic properties, such as summation and products of roots.
Explicit Formula for nth Roots of Unity
By equating $z^n=1$, and using polar representation, the general form is established as:
$z_k = e^{\frac{2\pi i k}{n}}$ for $k = 0, 1, \ldots, n-1$
Alternatively, $z_k = \cos\left( \frac{2\pi k}{n} \right) + i \sin\left( \frac{2\pi k}{n} \right)$. Each distinct $k$ produces a distinct solution on the unit circle.
Solved Examples: nth Roots of Unity
To illustrate, consider the calculation of the fifth roots of unity. Solve $z^5 = 1$ by expressing roots as $z_k = e^{\frac{2\pi i k}{5}}$ for $k = 0$ to $4$.
The roots are:
- $z_0 = 1$
- $z_1 = e^{\frac{2\pi i}{5}} = \cos \frac{2\pi}{5} + i \sin \frac{2\pi}{5}$
- $z_2 = e^{\frac{4\pi i}{5}} = \cos \frac{4\pi}{5} + i \sin \frac{4\pi}{5}$
- $z_3 = e^{\frac{6\pi i}{5}} = \cos \frac{6\pi}{5} + i \sin \frac{6\pi}{5}$
- $z_4 = e^{\frac{8\pi i}{5}} = \cos \frac{8\pi}{5} + i \sin \frac{8\pi}{5}$
Similarly, for $n=4$, the fourth roots of unity are $1$, $i$, $-1$, and $-i$. Each case can be worked out directly from the formula.
Primitive nth Roots of Unity
A primitive nth root of unity is a root $\omega = e^{\frac{2\pi i}{n}}$ such that its powers $\omega, \omega^2, \ldots, \omega^{n-1}$ exhaust all $n$ roots before cycling back to $1$. Formally, $\omega$ is primitive if no lower positive power equals $1$ except the $n$th.
For any $n$, the set $\{1, \omega, \omega^2, \ldots, \omega^{n-1}\}$ captures all roots of unity, where $\omega$ is any primitive root.
Algebraic Properties: Sum and Product of Roots
The sum of all nth roots of unity is zero, a consequence of their symmetric distribution. Let $\omega = e^{\frac{2\pi i}{n}}$, then
$1 + \omega + \omega^2 + \cdots + \omega^{n-1} = \dfrac{\omega^n - 1}{\omega - 1} = \dfrac{1-1}{\omega-1} = 0$
The product of all nth roots of unity is $(-1)^{n-1}$. This can be established using properties of symmetric polynomials or by noting the constant term in the factorization $x^n - 1 = 0$.
General nth Roots of Complex Numbers Using De Moivre’s Theorem
The process of extracting nth roots from an arbitrary complex number $z = r e^{i\theta}$ follows De Moivre’s Theorem. The $n$ distinct roots of $z$ are:
$w_k = r^{1/n} \left[ \cos\left( \dfrac{\theta + 2\pi k}{n} \right) + i\,\sin\left( \dfrac{\theta + 2\pi k}{n} \right) \right],$ for $k = 0, 1, ..., n-1$.
When $z = 1$, the above produces precisely the $n$th roots of unity as previously described.
Special Cases and Further Applications
For $n = 2$ (square roots), the roots are $1$ and $-1$. For $n = 3$ (cube roots), the solutions are $1$, $-\dfrac{1}{2} + i\dfrac{\sqrt{3}}{2}$, and $-\dfrac{1}{2} - i\dfrac{\sqrt{3}}{2}$.
Roots of unity feature prominently in polynomial equations, cyclic sums, and the discrete Fourier transform. Their properties greatly simplify many algebraic calculations and trigonometric summations.
Further utility is seen in Mock Test Series for mathematical practice involving complex numbers.
Key Summary of De Moivre’s Theorem and nth Roots of Unity
- De Moivre’s Theorem connects powers and roots of complex numbers to trigonometric identities
- nth roots of unity are $n$ points equally spaced on the unit circle in the complex plane
- The sum of all nth roots of unity is always zero
- The product of all nth roots of unity is $(-1)^{n-1}$
- Primitive roots are those whose smallest positive power returning unity is $n$ itself
This foundational understanding supports complex problem-solving in JEE Main mathematics topics, and finds direct relevance in many other branches of mathematics.
FAQs on Understanding De Moivre's Theorem and Nth Roots of Unity
1. What is De Moivre's Theorem in trigonometry?
De Moivre's Theorem provides a formula to raise complex numbers in polar form to any integer power quickly.
Key points include:
- It states: (cos θ + i sin θ)ⁿ = cos nθ + i sin nθ, where n is an integer.
- Used to simplify calculations with complex numbers and trigonometric expressions.
- Helpful for finding nth roots of unity and expanding expressions involving powers of cosines and sines.
2. What are the nth roots of unity?
Nth roots of unity are complex numbers that give 1 when raised to the power of n.
Key facts:
- For any positive integer n, the nth roots are: 1, ω, ω², ..., ωⁿ⁻¹ where ω = cos(2π/n) + i sin(2π/n).
- They are equally spaced points on the unit circle in the complex plane.
- They satisfy the equation xⁿ = 1.
- Nth roots of unity form significant examples in algebra and are frequently asked in exams.
3. How do you use De Moivre's Theorem to find the nth roots of a complex number?
De Moivre's Theorem helps find nth roots by expressing the number in polar form and dividing the angle by n.
Follow these steps:
- Write the number as r (cos θ + i sin θ).
- The nth roots are r1/n[cos((θ + 2πk)/n) + i sin((θ + 2πk)/n)], for k = 0, 1,..., n-1.
- This formula gives all distinct nth roots on the complex plane.
4. State De Moivre's Theorem with proof.
De Moivre's Theorem states that (cos θ + i sin θ)ⁿ = cos nθ + i sin nθ for any integer n.
Proof outline:
- Base case (n=1): Directly true.
- Assume for n, then for n+1: (cos θ + i sin θ)ⁿ⁺¹ = [cos nθ + i sin nθ][cos θ + i sin θ]
- After expansion using trigonometric identities, the result holds for n+1 too (by mathematical induction).
5. What are the applications of De Moivre's Theorem?
De Moivre's Theorem is widely used in solving and simplifying problems involving complex numbers.
Main uses:
- Raising complex numbers to integer powers.
- Calculating nth roots of unity.
- Deriving trigonometric identities and expansions.
- Simplifying expressions involving sines and cosines to higher powers.
6. Explain the geometric representation of nth roots of unity.
Nth roots of unity are represented as points equally spaced on the unit circle in the complex plane.
Key features:
- All roots are at a distance of 1 from the origin.
- They form the vertices of a regular n-sided polygon inscribed in the circle.
- The angle between adjacent roots is 2π/n radians.
7. What are the important properties of nth roots of unity?
Nth roots of unity have several key properties important for competitive and board examinations.
Main properties:
- Sum of all nth roots of unity equals zero.
- Product of all nth roots of unity is +1 for odd n, −1 for even n.
- All roots except 1 are complex numbers.
- They are solutions to the equation xⁿ = 1.
8. How do you expand (cos θ + i sin θ)^n using De Moivre's Theorem?
De Moivre's Theorem allows direct expansion of (cos θ + i sin θ)^n.
Expansion steps:
- Express as cos nθ + i sin nθ.
- When required, use the binomial theorem for more detailed form.
- This expansion is the basis for reducing higher power trigonometric expressions.
9. Can De Moivre's Theorem be used for non-integer powers?
While De Moivre's Theorem is primarily for integer powers, it can be adapted for rational exponents while considering multi-valued complex functions.
Details:
- For fractional powers (1/n), use the nth root formula for complex numbers.
- It produces multiple values as complex roots exist for all branches.
- This extension is relevant for advanced problem-solving in competitive maths.
10. Find all cube roots of unity using De Moivre's Theorem.
The three cube roots of unity can be found by solving x³ = 1 using De Moivre's Theorem.
They are:
- 1 (real root),
- ω = cos(2π/3) + i sin(2π/3) = −1/2 + i√3/2,
- ω² = cos(4π/3) + i sin(4π/3) = −1/2 − i√3/2.
























