NCERT Solutions for Class 11 Maths Chapter 12 - In Hindi

प्रश्नावली 12.1

1. एक बिन्दु \[x\,\,\, - \,\]अक्ष पर स्थित है। इस के \[y\,\,\, - \,\] निर्देशांक तथा \[z\,\,\, - \,\] निर्देशांक क्या है ?

उत्तर: \[x\,\,\, - \,\] अक्ष पर किसी बिन्दु के निर्देशांक $\left({\,\,x\,\,,\,\,0\,\,,\,\,0\,\,} \right)$ होते हैं जिसमें $y\,\, = \,\,0\,\,,\,\,z\,\, = \,\,0\,\,.$

2. एक बिन्दु $x$ तल में है। इसके $y\,\, - $ निर्देशांक के बारे में आप क्या कह सकते हैं?

उत्तर: $x\,\,z$ तल $y\,\, - $ निर्देशांक $0$ होता है। इस तल का बिन्दु $\left( {\,x\,\,,\,\,0\,\,,\,\,z\,} \right)$ के रूप में होता है।

3. अष्टाशों के नाम बताइए, जिनमें निम्नलिखित बिन्दु स्थित हैं:

$\mathbf{(\,\,1\,\,,\,\,2\,\,,\,\,3\,\,)\,\,,\,\,(\,\,4\,\,,\,\, - \,\,2\,\,,\,\,3\,\,)\,\,,\,\,(\,\,4\,\,,\,\, - \,\,2\,\,,\,\, - \,\,5\,\,)\,\,,\,\,(\,\,4\,\,,\,\,2\,\,,\,\, - \,\,5\,\,)\,\,,\,\,(\, - \,\,4\,\,,\,\,2\,\,,\,\, - \,\,5\,\,)\,\,,\,\,(\,\, - \,\,4\,\,,\,\,2\,\,,\,\,5\,\,)\,\,,\,\,}$

$\,athbf{(\,\, - \,\,3\,\,,\,\, - \,\,1\,\,,\,\,6\,\,)\,\,,\,\,(\,\,2\,\,,\,\, - \,\,4\,\,,\,\, - \,\,7\,\,)}$

उत्तर: दिए गए बिंदुओं के अंश है :

\[(i)\,\,\,\,(1,2,3)\,\, - \,\,XOYZ\,\, - \]  पहला 

\[(ii)\,\,\,\,(4, - 2,3)\,\, - \,\,{\text{XOYZ}}\,\, - \]  चौथा 

\[(iii)\,\,\,\,(4,2, - 5)\,\, - \,XOY'Z'\,\, - \]  आठवाँ 

\[(iv)\,\,\,\,(4,2, - 5)\,\, - \,\,XOYZ'\,\, - \]   पाचवाँ 

\[(v)\,\,\,\,\,( - 4,2, - 5)\,\, - \,\,XOYZ'\,\, - \]   छठा 

\[(vi)\,\,\,\,( - 4,2,5)\,\, - \,\,(XOYZ)\,\, - \]   दूसरा 

\[(vii)\,\,\,\,( - 3, - 1,6)\,\, - \,\,(XOY'Z)\,\, - \]  तीसरा 

\[(viii)\,\,\,(2, - 4. - 7)\,\, - \,\,(XOY'Z')\,\, - \]  आठवाँ 

4. रिक्त स्थानों की पूर्ति कीजिए:

(i)$x\,\, - $ अक्ष और $y\,\, - \,$ अक्ष दोनों एक साथ मिल कर एक तल बनाते हैं, उस तल को......कहते हैं।

उत्तर :  $X\,\,Y\,\, - $ तल  |

(ii). $X\,\,Y\,\, - $तल में एक बिन्दु के निर्देशांक........ रूप के होते हैं।

उत्तर :  $x\,\,,\,\,y\,\,,\,\,o$

(iii). निर्देशांक तल अंतरिक्ष को......... अष्टांश में विभाजित करते हैं।

उत्तर :  $8$

प्रश्नावली 12.2

1. निम्लिखित बिंदु -युग्मों के बीच की दूरी ज्ञात कीजिए:

(i). $\mathbf{\left( {\,\,2\,\,,\,\,3\,\,,\,\,5\,\,} \right)}$  और $\mathbf{\left( {\,4\,,\,\,3\,\,,\,\,1\,} \right)}$

उत्तर: $\left( {\,\,2\,\,,\,\,3\,\,,\,\,5\,\,} \right)$  और $\left( {\,4\,,\,\,3\,\,,\,\,1\,} \right)$

दो बिन्दु $\left( {\,{x_1},{y_1},{z_1}\,} \right)$ और  $\left( {\,{x_2},{y_2},{z_2}\,} \right)$ के बीच की दूरी 

$\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2} + {{\left( {{z_2} - {z_1}} \right)}^2}} $

बिन्दु $\left( {\,\,2\,\,,\,\,3\,\,,\,\,5\,\,} \right)$ और  $\left( {\,4\,,\,\,3\,\,,\,\,1\,} \right)$ के बीच की दूरी

$= \sqrt {{{(4 - 2)}^2} + {{(3 - 3)}^2} + {{(1 - 5)}^2}}$

$= \sqrt {{2^2} + {0^2} + {4^2}}$

$= \sqrt {4 + 16}$

$= \sqrt {20}$

$= 2\sqrt 5$ 

(ii). $\mathbf{\left( {\,\, - \,\,3\,\,,\,\,7\,\,,\,\,2\,\,} \right)}$ और $\mathbf{\left( {\,\,2\,\,,\,\,4\,\,,\,\, - \,\,1\,} \right)}$

उत्तर:   $\left( {\,\, - \,\,3\,\,,\,\,7\,\,,\,\,2\,\,} \right)$ और $\left( {\,\,2\,\,,\,\,4\,\,,\,\, - \,\,1\,} \right)$

दो बिन्दु $\left( {\,{x_1},{y_1},{z_1}\,} \right)$ और  $\left( {\,{x_2},{y_2},{z_2}\,} \right)$ के बीच की दूरी 

$\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2} + {{\left( {{z_2} - {z_1}} \right)}^2}} $

बिन्दु $\left( {\,\, - \,\,3\,\,,\,\,7\,\,,\,\,2\,\,} \right)$ और $\left( {\,\,2\,\,,\,\,4\,\,,\,\, - \,\,1\,} \right)$ के बीच की दूरी

$= \sqrt {{{(2 + 3)}^2} + {{(4 - 7)}^2} + {{(-1 - 2)}^2}}$

$= \sqrt {25 + 9 + 9}$

$= \sqrt {43}$ 

(iii). $\mathbf{\left( {\,\, - \,\,1\,\,,\,\,3\,\,,\,\, - \,4\,\,} \right)$ और $\left( {\,\,1\,\,,\,\, - \,3\,\,,\,\,4\,} \right)}$

उत्तर:  $\left( {\,\, - \,\,1\,\,,\,\,3\,\,,\,\, - \,4\,\,} \right)$ और  $\left( {\,\,1\,\,,\,\, - \,3\,\,,\,\,4\,} \right)$

दो बिन्दु $\left( {\,{x_1},{y_1},{z_1}\,} \right)$ और  $\left( {\,{x_2},{y_2},{z_2}\,} \right)$ के बीच की दूरी 

$\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2} + {{\left( {{z_2} - {z_1}} \right)}^2}} $

बिन्दु $\left( {\,\, - \,\,1\,\,,\,\,3\,\,,\,\, - \,4\,\,} \right)$ और $\left( {\,\,1\,\,,\,\, - \,3\,\,,\,\,4\,} \right)$ के बीच की दूरी

$= \,\,\sqrt {\,\,{{(\,\,1\,\, + \,\,1\,\,\,)}^2}\,\, + \,\,\,{{(\,\, - \,\,3\,\, - \,\,3\,\,)}^2}\,\, + \,\,{{(\,4\, + \,4\,)}^2}}$

$= \,\,\sqrt {\,4\,\, + \,\,36\,\, + \,\,64}$

$= \,\,\sqrt {\,\,104}$

$= \,\,2\,\,\sqrt {\,\,26}$ 

(iv). $\mathbf{\left( {\,\,2\,\,,\,\, - \,\,1\,\,,\,\,3\,\,} \right)}$ और $\mathbf{\left( {\,\, - \,\,2\,\,,\,\,1\,\,,\,3\,\,} \right)}$

उत्तर: $\left( {\,\,2\,\,,\,\, - \,\,1\,\,,\,\,3\,\,} \right)$ और $\left( {\,\, - \,\,2\,\,,\,\,1\,\,,\,3\,\,} \right)$

दो बिन्दु $\left( {\,{x_1},{y_1},{z_1}\,} \right)$ और  $\left( {\,{x_2},{y_2},{z_2}\,} \right)$ के बीच की दूरी 

$\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2} + {{\left( {{z_2} - {z_1}} \right)}^2}} $

बिन्दु $\left( {\,\,2\,\,,\,\, - \,\,1\,\,,\,\,3\,\,} \right)$ और $\left( {\,\, - \,\,2\,\,,\,\,1\,\,,\,3\,\,} \right)$ के बीच की दूरी

$= \,\,\,\sqrt {\,{{(\, - 2 - 2\,)}^2}\,\, + \,\,{{(\,1 + 1\,)}^2}\,\, + \,\,{{(\,3 - 3\,)}^2}}$

$= \,\,\,\sqrt {\,16\,\, + \,\,4\,\, + \,\,0}$

$= \,\,\,\sqrt {\,20}$

$= \,\,\,2\,\sqrt {\,5}$ 

2. दर्शाइए कि \[\mathbf{{\text{(}}\,\,{\text{ - }}\,\,{\text{2}}\,\,{\text{,}}\,\,{\text{3}}\,\,{\text{,}}\,\,{\text{5}}\,\,{\text{)}}\,\,{\text{,}}\,\,{\text{(}}\,\,{\text{1}}\,\,{\text{,}}\,\,{\text{2}}\,\,{\text{,}}\,\,{\text{3}}\,\,{\text{)}}}\] बिंदु और \[{\text{(}}\,\,{\text{7}}\,\,{\text{,}}\,\,{\text{0}}\,\,{\text{,}}\,\,{\text{ - }}\,\,{\text{1}}\,\,{\text{)}}\] संरेख हैं। 

उत्तर: मान लीजिए बिन्दु  \[{\text{A}}\,\,{\text{ = }}\,\,{\text{(}}\,\,{\text{ - }}\,\,{\text{2}}\,\,{\text{,}}\,\,{\text{3}}\,\,{\text{,}}\,\,{\text{5}}\,\,{\text{)}}\,\] और  \[B\,\, = \,\,\,{\text{(}}\,\,{\text{1}}\,\,{\text{,}}\,\,{\text{2}}\,\,{\text{,}}\,\,{\text{3}}\,\,{\text{)}}\] के बीच की दूरी 

$A\,\,B\,\, = \,\,\sqrt {\,\,{{(\,\,1\,\, + \,\,2\,\,)}^2}\,\, + \,\,{{(\,\,2\,\, - \,\,3\,\,)}^2}\,\, + \,\,{{(\,\,3\,\, - \,\,5\,\,)}^2}}$

$= \,\,\sqrt {\,\,9\,\, + \,\,1\,\, + \,\,4}$

$= \,\,\sqrt {\,\,14}$ 

बिन्दु   \[B\,\, = \,\,\,{\text{(}}\,\,{\text{1}}\,\,{\text{,}}\,\,{\text{2}}\,\,{\text{,}}\,\,{\text{3}}\,\,{\text{)}}\] और  \[{\text{C}}\,\,{\text{ = }}\,\,{\text{(}}\,\,{\text{7}}\,\,{\text{,}}\,\,{\text{0}}\,\,{\text{,}}\,\,{\text{ - }}\,\,{\text{1}}\,\,{\text{)}}\]  के बीच की दूरी

$B\,\,C\,\, = \,\,\sqrt {\,\,{{(\,\,1\,\, + \,\,2\,\,)}^2}\,\, + \,\,{{(\,\,2\,\, - \,\,3\,\,)}^2}\,\, + \,\,{{(\,\,3\,\, - \,\,5\,\,)}^2}}$

$= \,\,\sqrt {\,36\,\, + \,\,4\,\, + \,\,16}$

$= \,\,\sqrt {\,56}$

$= \,\,2\,\,\sqrt {\,14}$ 

बिन्दु   \[{\text{A}}\,\,{\text{ = }}\,\,{\text{(}}\,\,{\text{ - }}\,\,{\text{2}}\,\,{\text{,}}\,\,{\text{3}}\,\,{\text{,}}\,\,{\text{5}}\,\,{\text{)}}\,\] और  \[{\text{C}}\,\,{\text{ = }}\,\,{\text{(}}\,\,{\text{7}}\,\,{\text{,}}\,\,{\text{0}}\,\,{\text{,}}\,\,{\text{ - }}\,\,{\text{1}}\,\,{\text{)}}\]  के बीच की दूरी

$A\,\,C\,\, = \,\,\sqrt {\,\,{{(\,7 + 2\,)}^2}\,\, + \,\,{{(\,0 - 3\,)}^2}\,\, + \,\,{{(\, - 1 - 5\,)}^2}} $

$ = \,\,\sqrt {\,\,81\,\, + \,\,9\,\, + \,\,36} $

$ = \,\,\sqrt {\,\,126} $

$ = \,\,3\,\,\sqrt {\,\,14} $

अब $A\,B\,\, + \,\,B\,C$ को जोड़ने के बाद 

$A\,B\,\, + \,\,B\,C\,\, = \,\,\sqrt {\,\,14} \,\, + \,\,2\,\,\sqrt {\,\,14}$

 $= \,\,3\,\,\sqrt {\,\,14}$ 

जैसा हमें पता है कि ${\text{A}}\,\,{\text{C}}\,\,{\text{ = }}\,\,{\text{3}}\,\,\sqrt {\,\,14} $

यहाँ $A\,B\,\, + \,\,B\,C\,\, = \,\,A\,\,C$

अत: बिन्दु ${\text{A}}\,\,{\text{.}}\,\,{\text{B}}\,\,{\text{.}}\,\,{\text{C}}$संरेख हैं |

3. निम्लिखित को सत्यपति कीजिए:

(i). \[\mathbf{{\text{(}}\,\,{\text{0}}\,\,{\text{,}}\,\,{\text{7}}\,\,{\text{,}}\,\,{\text{ - }}\,\,{\text{10}}\,\,{\text{)}}\,\,{\text{,}}\,\,{\text{(}}\,\,{\text{1}}\,\,{\text{,}}\,\,{\text{6}}\,\,{\text{,}}\,\,{\text{ - }}\,\,{\text{6}}\,\,{\text{)}}\,\]और \[\,{\text{(}}\,\,{\text{4}}\,\,{\text{,}}\,\,{\text{9}}\,\,{\text{,}}\,\,{\text{ - }}\,\,{\text{6}}\,\,{\text{)}}}\] एक समद्विबाहु त्रिभुज के शीर्ष हैं।

उत्तर: माना त्रिभुज $A\,\,B\,\,C$ के शीर्ष \[{\text{(}}\,\,{\text{0}}\,\,{\text{,}}\,\,{\text{7}}\,\,{\text{,}}\,\,{\text{ - }}\,\,{\text{10}}\,\,{\text{)}}\,\,{\text{,}}\,\,{\text{(}}\,\,{\text{1}}\,\,{\text{,}}\,\,{\text{6}}\,\,{\text{,}}\,\,{\text{ - }}\,\,{\text{6}}\,\,{\text{)}}\,\]और\[\,{\text{(}}\,\,{\text{4}}\,\,{\text{,}}\,\,{\text{9}}\,\,{\text{,}}\,\,{\text{ - }}\,\,{\text{6}}\,\,{\text{)}}\] हैं |

अब , 

$A\,\,B\,\, = \,\,\sqrt {\,\,{{(\,1\,\, - \,\,0\,)}^{2\,}}\,\, + \,\,{{(\,6\,\, - \,\,7\,)}^2}\, + \,\,{{(\, - \,\,6\,\, + \,\,10\,)}^2}}$

$= \sqrt {\,\,1\,\, + \,\,1\,\, + \,\,16}$

$= \,\,\sqrt {\,\,18}$

$= \,\,3\,\,\sqrt {\,2} \,$ 

अब ,

$B\,\,C\,\, = \sqrt {\,{{(\,4\,\, - \,\,1\,)}^2}\,\, + \,\,{{(\,9\,\, - \,\,6\,)}^2}\,\, + \,\,{{(\, - \,\,6\,\, + \,\,6\,\,)}^2}}$

$= \,\,\sqrt {\,\,9\,\, + \,\,9}$

$= \,\,\sqrt {\,\,18}$

$= \,\,3\,\,\sqrt {\,2}$ 

हमें पता चला कि यहाँ ${\text{A}}\,\,{\text{B}}\,\,{\text{ = }}\,\,{\text{B}}\,\,{\text{C}}$ हैं |

अत: दिए गए शीर्ष समद्विबाहु त्रिभुज के हैं |

(ii). \[\mathbf{{\text{ (}}\,\,{\text{0}}\,\,{\text{,}}\,\,{\text{7}}\,\,{\text{,}}\,\,{\text{10}}\,\,{\text{)}}\,\,{\text{,}}\,\,{\text{(}}\,\,{\text{ - }}\,\,{\text{1}}\,\,{\text{,}}\,\,{\text{6}}\,\,{\text{,}}\,\,{\text{6}}\,\,{\text{)}}\,\]और \[\,{\text{(}}\,\,{\text{ - }}\,\,{\text{4}}\,\,{\text{,}}\,\,{\text{9}}\,\,{\text{,}}\,\,{\text{6}}\,\,{\text{)}}}\] एक समकोण त्रिभुज के शीर्ष हैं।

उत्तर : माना त्रिभुज $P\,\,Q\,\,R$ के शीर्ष \[{\text{ (}}\,\,{\text{0}}\,\,{\text{,}}\,\,{\text{7}}\,\,{\text{,}}\,\,{\text{10}}\,\,{\text{)}}\,\,{\text{,}}\,\,{\text{(}}\,\,{\text{ - }}\,\,{\text{1}}\,\,{\text{,}}\,\,{\text{6}}\,\,{\text{,}}\,\,{\text{6}}\,\,{\text{)}}\,\]और\[\,{\text{(}}\,\,{\text{ - }}\,\,{\text{4}}\,\,{\text{,}}\,\,{\text{9}}\,\,{\text{,}}\,\,{\text{6}}\,\,{\text{)}}\] हैं|

अब , 

$P\,\,{Q^2}\,\, = \,\,{(\, - 1\, - 1\,)^2}\,\, + \,\,{(\,6\, - \,7\,)^2}\,\, + \,\,{(\,6 - 10\,)^2} $

$= \,\,1\,\, + \,\,1\,\, + \,\,16 $

$= 1\,\,8 $ 

अब ,

$Q\,\,{R^2}\,\, = \,\,{(\, - 4\,\, + \,\,1\,)^2}\,\, + \,\,{(\,9\,\, - \,\,6\,)^2}\,\, + \,\,{(\,6\,\, - \,\,6\,)^2}$

$= \,\,9\,\, + \,\,9\,\, + \,\,0\,\, = \,\,18$ 

यहाँ , 

$P\,\,{R^2}\,\, + \,\,Q\,\,{R^2}\,\, = \,\,18\,\, + \,\,18\,\,\, = \,\,36 $

$\therefore \,\,P\,\,R\,{\,^{2\,}}\,\, = \,\,36 $

 $P\,\,{Q^2}\,\, + \,\,Q\,\,{R^2}\,\, = \,\,P{R^2} $ 

अत: दिए गए शीर्ष समकोण त्रिभुज के हैं।

(iii).\[\mathbf{{\text{(}}\,\,{\text{-}}\,\,{\text{1}}\,\,{\text{,}}\,\,{\text{2}}\,\,{\text{,}}\,\,{\text{1}}\,\,{\text{)}}\,\,{\text{,}}\,\,{\text{(}}\,\,{\text{1}}\,\,{\text{,}}\,\,{\text{ - }}\,\,{\text{2}}\,\,{\text{,}}\,\,{\text{5}}\,\,{\text{)}}\,\,{\text{,}}\,\,{\text{(}}\,\,{\text{4}}\,\,{\text{,}}\,\,{\text{ - }}\,\,{\text{7}}\,\,{\text{,}}\,\,{\text{8}}\,\,{\text{)}}\,}\]और \[\mathbf{\,{\text{(}}\,\,{\text{2}}\,\,{\text{,}}\,\,{\text{ - }}\,\,{\text{3}}\,\,{\text{,}}\,\,{\text{4}}\,\,{\text{)}}}\] एक समांतर चतुर्भुज के शीर्ष हैं।

उत्तर :  माना त्रिभुज $A\,\,B\,\,C\,\,D$ के शीर्ष \[{\text{A}}\,\,{\text{(}}\,\,{\text{ - }}\,\,{\text{1}}\,\,{\text{,}}\,\,{\text{2}}\,\,{\text{,}}\,\,{\text{1}}\,\,{\text{)}}\,\,{\text{,}}\,B\,\,{\text{(}}\,\,{\text{1}}\,\,{\text{,}}\,\,{\text{ - }}\,\,{\text{2}}\,\,{\text{,}}\,\,{\text{5}}\,\,{\text{)}}\,\,{\text{,}}\,C\,\,{\text{(}}\,\,{\text{4}}\,\,{\text{,}}\,\,{\text{ - }}\,\,{\text{7}}\,\,{\text{,}}\,\,{\text{8}}\,\,{\text{)}}\,\]और \[D\,\,\,{\text{(}}\,\,{\text{2}}\,\,{\text{,}}\,\,{\text{ - }}\,\,{\text{3}}\,\,{\text{,}}\,\,{\text{4}}\,\,{\text{)}}\] हैं | अब ,

$A\,\,B{\,^2}\,\, = \,\,{(\,\,1\,\, + \,\,1\,\,)^2}\,\, + \,\,{(\,\, - \,\,2\,\, - \,\,2\,\,)^2}\,\, + \,\,{(\,\,5\,\, - \,\,1\,\,)^2} $

$= \,\,4\,\, + \,\,16\,\, + \,\,16\,\, $

$= \,\,36 $ 

अब ,

$B\,\,{C^2}\,\, = \,\,{(\,\,4\,\, - \,\,1\,\,)^2}\,\, + \,\,{(\,\, - \,\,2\,\, + \,\,2\,\,)^2}\,\, + \,\,{(\,\,8\,\, - \,\,5\,\,)^2} $

$= \,\,9\,\, + \,\,25\,\, + \,\,9 $

$= \,\,43 $ 

अब ,

$C\,\,{D^2}\,\, = \,\,{(\,\,2\,\, - \,\,4\,\,)^2}\,\, + \,\,{(\,\, - \,\,3\,\, + \,\,7\,\,)^2}\,\, + \,\,{(\,\,4\,\, - \,\,8\,\,)^2} $

$= \,\,4\,\, + \,\,16\,\, + \,\,16 $

$= \,\,36 $ 

अब ,

$A\,\,{D^2}\,\, = \,\,{(\,\,2\,\, + \,\,1\,\,)^2}\,\, + \,\,{(\,\, - \,\,3\,\, - \,\,2\,\,)^2}\,\, + \,\,{(\,\,4\,\, - \,\,1\,\,)^2} $

$= \,\,9\,\, + \,\,25\,\, + \,\,9 $

$= \,\,43 $ 

जैसा हमें पता चला कि 

$A\,\,{B^2} = \,\,C\,\,{D^2}$ और     $B\,\,{C^2}\,\, = \,\,A{D^2}$

$A\,\,B\,\, = \,\,C\,\,D$  और  $B\,\,C\,\, = \,\,AD$

अत: दिए गए बिन्दु एक समांतर चतुर्भुज के हैं |

4. ऐसे बिंदुओं के समुच्चय का समीकरण ज्ञात कीजिए जो \[\mathbf{{\text{(}}\,\,{\text{1}}\,\,{\text{,}}\,\,{\text{2}}\,\,{\text{,}}\,\,{\text{3}}\,\,{\text{)}}\,\,}\] और \[\mathbf{{\text{(}}\,\,{\text{3}}\,\,{\text{,}}\,\,{\text{2}}\,\,{\text{,}}\,\,{\text{ - }}\,\,{\text{1}}\,\,{\text{)}}}\] बिंदु से समदूरस्थ हैं।

उत्तर : माना बिन्दु बिन्दु और बिन्दु से समान दूरी पर है |

अत: \[P\,\,A\,\, = \,\,P\,\,B\]

अब , \[P\,\,{A^2}\,\, = \,\,P\,\,{B^2}\]

${(\,x - 1\,)^2} + {(\,y - 2\,)^2} + {(\,z - 3\,)^2}\,\, = \,\,{(\,x - 3\,)^2} + {(\,y - 2\,)^2} + {(\,z + 1\,)^2} $

$\Rightarrow \,\,\,\left( {\,{x^2} - 2x + 1\,} \right) + \left( {\,{z^2} - 6z + 9\,} \right)\,\, = \,\,\left( {\,{x^2} - 6x + 9\,} \right) + \left( {\,{z^2} + } \right.2z + 1\,) $

$\Rightarrow \,\,\, - 2x + 6x - 6z - 2z + 10 - 10\,\, = \,\,0 $

$\Rightarrow \,\,\,4x - 8z\,\, = \,\,0 $ 

अत: अभीष्ट समीकरण \[x\,\, - \,\,2\,\,z\,\, = \,\,0\]

5. बिंदुओं च् से बने समुच्चय का समीकरण ज्ञात कीजिए जिनकी बिंदुओं से \[\mathbf{{\text{A}}\,\,{\text{(}}\,\,{\text{4}}\,\,{\text{,}}\,\,{\text{0}}\,\,{\text{,}}\,\,{\text{0}}\,\,{\text{)}}\] और  \[{\text{B}}\,\,{\text{(}}\,\,{\text{ - }}\,\,{\text{4}}\,\,{\text{,}}\,\,{\text{0}}\,\,{\text{,}}\,\,{\text{0}}\,\,{\text{)}}\]दूरियों का योगफल \[{\text{10}}}\] है।

उत्तर: दिए गए बिन्दु \[{\text{A}}\,\,{\text{(}}\,\,{\text{4}}\,\,{\text{,}}\,\,{\text{0}}\,\,{\text{,}}\,\,{\text{0}}\,\,{\text{)}}\] और \[{\text{B}}\,\,{\text{(}}\,\,{\text{ - }}\,\,{\text{4}}\,\,{\text{,}}\,\,{\text{0}}\,\,{\text{,}}\,\,{\text{0}}\,\,{\text{)}}\] इस प्रकार है कि 

$P\,\,A\,\, + \,\,P\,\,B\,\, = \,\,10$

$\sqrt {{{(x - 4)}^2} + {{(y - 0)}^2} + {{(z - 0)}^2}} \,\,\, + \,\,\sqrt {{{(x + 4)}^2} + {{(y - 0)}^2} + {{(z - 0)}^2}} \,\,\,\, = \,\,\,\,\,10 $

 $\Rightarrow \,\,\sqrt {{x^2} + {y^2} + {y^2} - 8x + 16} \,\,\,\,\,\,\,\,\,\, = \,\,\,10 - \sqrt {{x^2} + {y^2} + {y^2} + 8x + 16}$ 

दोनों पक्षों का वर्ग करने पर ,

$\Rightarrow \,\,\,{x^2} + {y^2} + {y^2} - 8x + 16\,\,\, = \,\,\,100 + \left( {{x^2} + {y^2} + {y^2} - 8x + } \right.{\text{16) }} - 20\sqrt {{x^2} + {y^2} + {y^2} - 8x + 16}$

 $\Rightarrow \,\,\, - 16x - 100\,\,\, = \,\,\, - 20\sqrt {{x^2} + {y^2} + {y^2} + 8x + 16}$

 $\Rightarrow \,\,\,4x + 25\,\,\, = \,\,\,5\sqrt {{x^2} + {y^2} + {y^2} + 8x + 16}$ 

अत:  फिर से दोनों पक्षों का वर्ग करने पर ,

${(4x + 25)^2}\,\,\, = \,\,\,25\left( {{x^2} + {y^2} + {y^2} + 8x + 16} \right) $

 $\Rightarrow \,\,\,16{x^2} + 200x + 625\,\,\, = \,\,\,25{x^2} + 25{y^2} + 25{y^2} + 200x + 400 $

 $\Rightarrow \,\,\,9{x^2} + 25{y^2} + 25{z^2}\,\,\, = \,\,\,625 - 400 = 225 $ 

अत:  अभीष्ट समीकरण $9\,\,{x^2}\,\, + \,\,25\,\,{y^2}\,\, + \,\,25\,\,{z^2}\,\,\, = \,\,\,225$

प्रश्नावली 12.3

1. बिंदुओं $\mathbf{\left( {\,\, - \,\,2\,\,,\,\,3\,\,,\,\,5\,\,} \right)}$ और $\mathbf{\left( {\,\,1\,\,,\,\, - \,\,4\,\,,\,\,6\,\,} \right)}$ को मिलाने से बने रेखा खंड को अनुपात (i)  $\mathbf{2\,\,:\,\,3}$ में अंत: (ii) $\mathbf{2\,\,:\,\,3}$ में बाह्यतः विभाजित करने वाले बिंदु के निर्देशांक ज्ञात कीजिए।

उत्तर : (i) माना बिन्दुओं $A\,\,\left( {\,\, - \,\,2\,\,,\,\,3\,\,,\,\,5\,\,} \right)$ और $B\,\,\left( {\,\,1\,\,,\,\, - \,\,4\,\,,\,\,6\,\,} \right)$ को मिलाने से बने रेखाखण्ड $A\,\,B$ को $P\,\,\left( {\,\,X\,\,,\,\,Y\,\,,\,\,Z\,\,} \right)$ अनुपात $2\,\,:\,\,3$$$ में अंत विभाजित करता हो, तब बिन्दु  के निर्देशांक इस प्रकार-

$X = \,\,\,\dfrac{{(\,2 \times 1 + 3x\,\,(\, - 2\,)\,)}}{{2 + 3}}\,\,\,\,\, = \,\,\,\,\,\dfrac{{(\,2 - 6\,)}}{5}\,\,\,\,\, = \,\,\,\,\,\dfrac{{ - 4}}{5} $

$Y\,\,\, = \,\,\,\dfrac{{(\,2x\,\,(\, - 4\,\,) + 3 \times 3\,)}}{{2 + 3}}\,\,\,\,\, = \,\,\,\,\,\dfrac{{(\, - 8 + 9\,)}}{5}\,\,\,\,\,\, = \,\,\,\,\,\,\dfrac{1}{5} $

 $Z\,\,\, = \,\,\,\dfrac{{(\,2 \times 6 + 3 \times 5\,)}}{{2 + 3\,}}\,\,\,\,\, = \,\,\,\,\,\,\dfrac{{(\,12 + 15\,)}}{5}\,\,\,\,\, = \,\,\,\,\,\,\dfrac{{27}}{5} $ 

अत: बिन्दु ${\text{P}}$ के निर्देशांक $\left( {\,\,\dfrac{{ - 4}}{5}\,\,,\,\,\dfrac{1}{5}\,\,,\,\,\dfrac{{27}}{5}\,\,} \right)$ हैं |

(ii)  जब बिन्दु $P\,\,\left( {\,\,X\,\,,\,\,Y\,\,,\,\,Z\,\,} \right)$ रेखाखण्ड $A\,\,B$ के बाह्यतः ; विभाजित करता हो , तो निर्देशांक इस प्रकार होगे

$X\,\,\, = \,\,\,\dfrac{{(\,2 \times 1 - 3x\,(\, - 2\,)\,)}}{{2 - 3}}\,\,\,\,\, = \,\,\,\,\dfrac{{(\,2 + 6\,)}}{{ - 1}}\,\,\,\,\,\,\,\,\,\,\, =  - 8 $

  $Y\,\,\, = \,\,\,\dfrac{{(\,2x\,(\, - 4\,) - 3 \times 3\,)}}{{2 - 3}}\,\,\,\,\, = \,\,\,\,\dfrac{{(\, - 8 - 9\,)}}{{ - 1}}\,\,\,\,\,\,\,\, = 17 $

  $Z\,\,\, = \,\,\,\dfrac{{(\,2 \times 6 - 3 \times 5\,)}}{{2 - 3}}\,\,\,\,\,\,\,\,\,\,\,\,\, = \,\,\,\,\dfrac{{(\,12 - 15\,)}}{{ - 1}}\,\,\,\,\,\,\,\, = 3 $ 

अत: बिन्दु ${\text{P}}$ के निर्देशांक $\left( {\,\, - 8\,\,,\,\,17\,\,,\,\,3\,\,} \right)$ हैं |

2. दिया गया है कि बिंदु $\mathbf{P\,\,\left( {\,\,3\,\,,\,\,2\,\,,\,\, - \,\,4\,\,} \right)\,\,,\,\,Q\,\,\left( {\,\,5\,\,,\,\,4\,\,,\,\, - \,\,6\,\,} \right)}$और $\mathbf{R\,\,\left( {\,\,9\,\,,\,\,8\,\,,\,\, - \,\,10\,\,} \right)\,}$ संरेख है। वह अनुपात ज्ञात कीजिए जिसमें को विभाजित करता है।

उत्तर : $x$ निर्देशांक , 

${\text{5}}\,\,\,{\text{ = }}\,\,\,\dfrac{{\left( {\,\,k\,\,*\,\,9\,\, + \,\,1\,\,*\,\,3\,\,} \right)}}{{k\,\, + \,\,1}}$

$\Rightarrow \,\,\,5\,\,(\,k + 1\,)\,\, = \,\,9\,k + 3 $

$\Rightarrow \,\,\,4\,k\,\, = \,\,5 - 3\,\,\,\,\,\,\,\,\,\,\, \Rightarrow \,\,\,\,\,\,k\,\, = \,\,\dfrac{2}{4}\, $

 $\Rightarrow \,\,\,k\,\, = \,\,\dfrac{1}{2} $ 

इसी प्रकार $y\,\, - $ निर्देशांक 

\[4\,\,\, = \,\,\dfrac{{(\,8\,k\, + \,2\,)}}{{k + \,1}}\]

$\Rightarrow \,\,\,\,4\,\,k\,\, + \,\,4\,\,\, = \,\,\,8\,\,k\,\, + \,\,2 $

$\Rightarrow \,\,\,\,8\,\,k\,\, - \,\,4\,\,k\,\,\, = \,\,\,4\,\,\, - \,\,2 $

$\Rightarrow \,\,\,\,4\,\,{\text{k}}\,\, = \,\,2 $

$\Rightarrow \,\,\,\,{\text{k}}\,\, = \,\,\dfrac{1}{2} $ 

अब इसी प्रकार $z\,\, - $ निर्देशांक

$- \,6\,\,\, = \,\,\,\dfrac{{(\, - 10\,\,k - 4\,)}}{{k + \,\,1}} $

$\Rightarrow \,\,\,6\,\,k\,\, + \,\,6\,\,\, = \,\,10\,\,k\,\, + \,\,4 $

$\Rightarrow \,\,\,10\,\,k\,\, - \,\,6\,\,k\,\,  = \,\,6\,\,\,- \,\,4 $

$\Rightarrow \,\,\,4\,\,k\,\, = \,\, \,\,2\,\,\,\,\,\,\,\,\,$ 

$\Rightarrow \,\,\,k\,\, = \,\,\dfrac{1}{2} $ 

अत: बिन्दु $P\,\,,\,\,Q\,\,,\,\,R$ संरेख हैं और $Q\,\,,\,\,P\,\,,\,\,R$  को  $1\,\,:\,\,2$ के अनुपात में विभाजित करता है |

3. बिंदुओं $\mathbf{\left( {\,\, - \,\,2\,\,,\,\,4\,\,,\,\,7\,\,} \right)}$और $\mathbf{\left( {\,\,3\,\,,\,\, - \,\,5\,\,,\,\,8\,\,} \right)}$ को मिलाने वाली रेखा खंड, $\mathbf{Y\,\,2\,\, -} $ तल द्वारा किस अनुपात में विभक्त होता है, उसे ज्ञात कीजिए।

उत्तर: मान लीजिए बिन्दु $P$  पर तल $Y\,\,Z$ रेखाखण्ड $A\,\,B$ को $k\,\,:\,\,1$ के अनुपात में प्रतिच्छेद करता है, तब $Y\,\,Z\,\, - $ तल पर प्रत्येक बिन्दु $\left( {\,\,o\,,\,\,y\,,\,\,z\,\,} \right)$के रूप में होगा।

$A\,,\,B$ के निर्देशांक क्रमश:  $\left( {\,\, - \,\,2\,\,,\,\,4\,\,,\,\,7\,\,} \right)$ और  $\left( {\,\,3\,\,,\,\, - \,\,5\,\,,\,\,8\,\,} \right)$है |

$0\,\,\, = \,\,\,\dfrac{{\left[ {\,k\,{\,^ \star }\,\,3\,\, + \,\,1\,{\,^{*\,\,}}(\,\, - \,\,2\,\,)\,} \right]\,}}{{k + 1}}\,\,\, = \,\,\,\dfrac{{(\,\,3\,\,k\,\, - \,\,2\,\,)}}{{k + 1}} $

$\Rightarrow \,\,\,\,3\,\,k\,\, - \,\,2\,\, = \,\,0{\text{ }}\,\,\,\,\,\,\,\,\,\,\, \Rightarrow \,\,k\,\, = \dfrac{2}{3} $ 

अत: $A\,\,B$ को $Y\,\,Z\,\, - $ तल $2\,\,:\,\,0$ के अनुपात में विभक्त करता है |

4. विभाजन सूत्र का प्रयोग करके दिखाइए कि बिंदु $\mathbf{{\text{A}}\,\,(\,\,2\,,\, - 3\,,\,\,4\,\,)\,\,,\,\,{\text{B}}\,\,(\, - 1\,,\,\,2\,\,,\,\,1\,\,)\,}$ तथा $\mathbf{C\,\,(\,\,\,0\,,\,\,1/3\,\,,\,\,2\,\,\,)}$ संरेख है।

उत्तर : माना  $A\,\,,\,\,B\,\,,\,\,C\,\,,$  सरेख हैं $B$, रेखाखण्ड $A\,\,C$को $k\,\,:\,\,1$ में विभाजित करता है। 

$- 1\,\, = \,\,\,\dfrac{{\left( {\,{k^ \star }0 + {1^*}2\,} \right)}}{{k + 1}} $

$\Rightarrow \,\,\,\, - k - 1\,\, = \,\,2 $

$ \Rightarrow \,\,\,\,k\,\, = \,\, - 3 $

$\bullet \,\,\,2 = \dfrac{{\left[ {{k^*}1/3 + {1^*}( - 3)} \right]}}{{k + 1}} $

$\Rightarrow \,\,\,\,2k + 2 = \dfrac{k}{{3 - 3}} $

$\Rightarrow \,\,\,\dfrac{{\,2k - k}}{3} =  - 3 - 2 $

$\Rightarrow \,\,\,\,\dfrac{5}{{3k}} =  - 5 $

$\Rightarrow \,\,\,\,k\,\, = \,\, - 3 $ 

और 

अत: $A\,\,,\,\,B\,\,,\,\,C\,\,,$ बिन्दु संरेख हैं |

5. \[\mathbf{{\text{P}}\,\,{\text{( 4 , 2 ,  -  6 )}}}\] और \[\mathbf{{\text{Q  (  10 ,  -  16 , 6 )}}}\]  के मिलाने वाली रेखा खंड \[\mathbf{{\text{P Q}}}\] को सम त्रि-माजित करने वाले बिंदुओं के निर्देशांक ज्ञात कीजिए |

उत्तर :

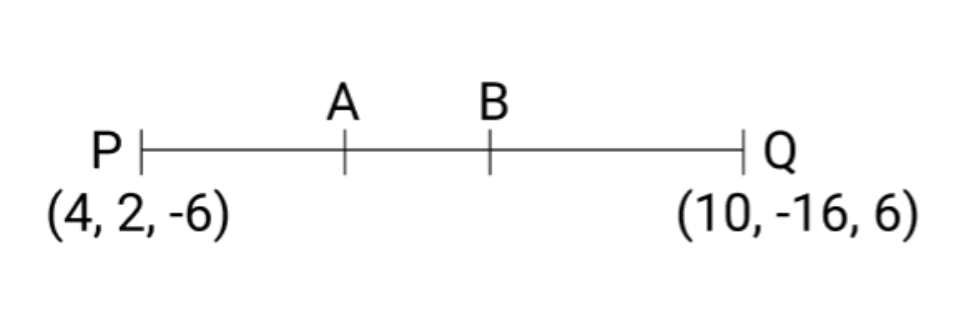
माना बिन्दु \[A\,\,,\,\,B\] रेखाखण्ड $P\,\,Q$ को $3$ समान भागों में विभाजित करती है।

बिन्दु $A$ , रेखाखण्ड $P\,\,Q$ को $1\,\,:\,\,2$ के अनुपात में विभाजित करता है। 

${\text{A}}\,\, = \,\,\left[ {\,\dfrac{{(\,1 \times 10 + 2 \times 4\,)}}{{1 + 2}}\,\,,\,\,\dfrac{{(\,1 \times (\, - 16\,) + 2 \times 2\,)}}{{1 + 2}}\,\,,\,\,\dfrac{{(\,1 \times 6 + 2{\text{x}}(\, - 6\,)\,)}}{{1 + 2}}\,} \right]\,\,\,$

$ \Rightarrow {\text{A}}\,\,\, = \,\,\left( {\,\dfrac{{18}}{3}\,,\, - \dfrac{{12}}{3}\,,\, - \dfrac{6}{3}\,} \right)$        या        $ \Rightarrow {\text{A}}\,(6, - 4, - 2)$

बिन्दु $B$ , रेखाखण्ड $P\,\,Q$ को $2\,\,:\,\,1$ के अनुपात में विभाजित करता है। 

$B$ के निर्देशांक

$B\,\,\left[ {\,\dfrac{{(\,2 \times 10 + 1 \times 4\,)}}{{2 + 1}},\dfrac{{(\,2x\,(\, - 16\,) + 1 \times 2\,)}}{{2 + 1}},\dfrac{{(\,2 \times 6 + 1x\,(\, - 6\,)\,)}}{{2 + 1}}\,} \right] $

$ = B\,\,(\,\,8\,, - 10\,,2\,\,) $ 

अत: $4$ तथा $B$ के निर्देशांक क्रमश: $\left( {\,6\,\,,\,\, - 4\,\,,\,\, - 2\,} \right)$ और  $\left( {\,\,8\,\,,\,\, - \,\,10\,\,,\,\,2\,\,} \right)$ हैं |

प्रश्नावली A1.2

1. समांतर चतुर्भुज के तीन शीर्ष \[\mathbf{A\,\,\left( {\,\,3\,\,,\,\, - 1\,\,,\,\,2\,\,} \right)\,\,,{\text{ }}B\,\,\left( {\,\,1\,\,,\,\,2\,\,,\,\, - 4\,} \right)\] व  \[C{\text{ }}\left( {\, - \,1\,\,,\,\,1\,\,,\,\,2\,\,} \right)}\] है। चौथे शीर्ष के निर्देशांक ज्ञात कीजिए ।

उत्तर: शीर्ष ${\text{A}}$ और $C$ क्रमश: \[\left( {\,\,3\,\,,\,\, - 1\,\,,\,\,2\,\,} \right)\,\,,\] \[\left( {\, - \,1\,\,,\,\,1\,\,,\,\,2\,\,} \right)\]  है |

${\text{A}}$ और $C$ मध्य बिन्दु के निर्देशांक $ = \,\,\,\left( {\,\dfrac{{3 - 1}}{2}\,\,,\,\,\dfrac{{ - 1 + 1}}{2}\,\,,\,\,\dfrac{{2 + 2}}{2}\,\,} \right)$

$ = \,\,\left( {\,\,1\,\,,\,\,0\,\,,\,\,2\,\,} \right)$

माना बिन्दु $D$ के निर्देशांक $\left( {\,\,x\,\,,\,\,y\,\,,\,\,z\,\,} \right)$ और बिन्दु $B$ के निर्देशांक $\left( {\,\,1\,\,,\,\,2\,\,,\,\, - \,\,4\,\,} \right)$ है |

$\therefore \,\,D\,B$ का मध्य बिन्दु $\left( {\,\,\dfrac{{x + 1}}{2}\,\,,\,\,\dfrac{{y + 2}}{2}\,\,,\,\,\dfrac{{z - 4}}{2}\,\,} \right)$

समांतर चतुर्भुज के विकरण एक दूसरे के $2$ समान भागों में बांटते है 

इसलिए 

$\left( {\,\,\dfrac{{x + 1}}{2} = 1\,\,,\,\,\dfrac{{y + 2}}{2} = 0\,\,,\,\,\dfrac{{z - 4}}{2} = 2\,} \right) $

$x\,\, = \,\,1\,\,,\,\,y\,\, = \,\, - 2\,\,,\,\,z\,\, = \,\,8 $ 

अत: बिन्दु के निर्देशांक $\left( {\,\,1\,\,,\,\, - 2\,\,,\,\,8\,\,} \right)$ है |

2. एक त्रिभुज के शीर्षों के निर्देशां क्रमशः \[\mathbf{A\,\,\left( {\,\,0,0,6\,\,} \right),B\,\,\left( {\,\,0,4,0\,\,} \right)}\] तथा \[\mathbf{C\,\,\left( {\,\,6,0,0\,\,} \right)}\]हैं। त्रिभुज की माध्यिकाओं की लंबाई ज्ञात कीजिए ।

उत्तर :

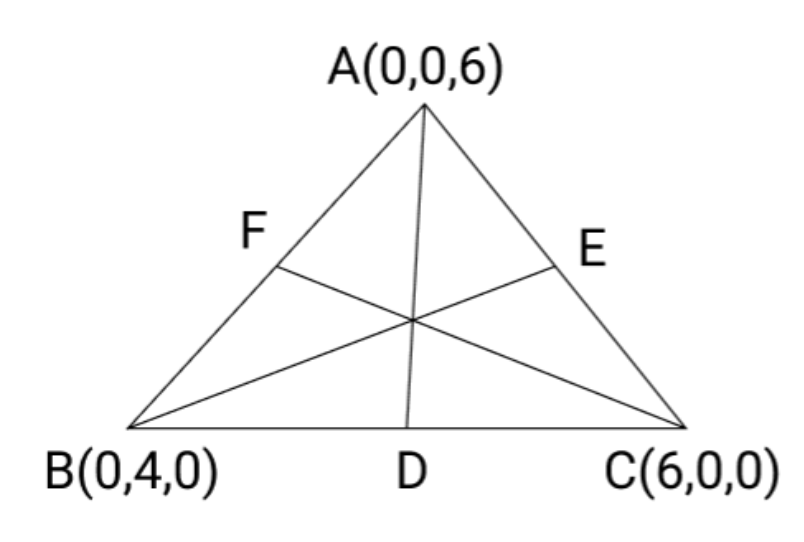
बिन्दु $B\,\,\left( {\,\,0\,\,,\,\,4\,\,,\,\,0\,} \right)$ और $C\,\,\,\left( {\,\,6\,\,,\,\,0\,\,,\,\,0\,\,} \right)$ को मिलाने वाला रेखाखण्ड का मध्य बिन्दु $D\,\,\left( {\,\,\dfrac{{0 + 6}}{2}\,\,,\,\,\dfrac{{4 + 0}}{2}\,\,,\,\,\dfrac{{0 + 0}}{2}\,\,} \right)$ है 

बिन्दु के $A$ निर्देशांक $\left( {\,\,0\,\,,\,\,0\,\,,\,\,6\,\,} \right)$ है 

त्रिभुज $A\,\,B\,\,$ के माध्यिका $A\,\,D$ की लम्बाई 

$ = \,\,\sqrt {\,\,{{(\,\,3 - 0\,\,)}^2}\,\, + \,\,\,{{(\,\,2 - 0\,\,)}^2}\,\, + \,\,{{(\,\,0 - 6\,\,)}^2}} $

$= \,\,\sqrt {\,\,9\,\, + \,\,4\,\, + \,\,36}$

$= \,\,\,\sqrt {\,\,49}$

$= \,\,7 $ 

$C$  और  $A$ के निर्देशांक $\left( {\,\,6\,\,,\,\,0\,\,,\,\,0\,} \right)$ और  \[\left( {\,\,0,0,6\,\,} \right)\] हैं |

$A\,\,C$ का मध्य बिन्दु $E$ \[\,\left( {\,\,\dfrac{{0 + 6}}{2}\,\,,\,\,\dfrac{{0 + 0}}{2}\,\,,\,\,\dfrac{{0 + 6}}{2}\,\,} \right)\]

$E\,\,\,\, = \,\,\,\,(\,\,3\,\,,\,\,0\,\,,\,\,3\,\,) $

$B\,\,\,\, = \,\,\,\,(\,\,0\,\,,\,\,4\,\,,\,\,0\,\,) $ 

त्रिभुज $A\,\,B\,\,C$ के माध्यिका $B\,\,E$ की लंबाई 

$= \,\,\,\sqrt {\,\,{{(\,\,3\,\, - \,\,0\,\,)}^2}\,\, + \,\,{{(\,\,0\,\, - \,\,4\,\,)}^2}\,\, + \,\,{{(\,\,3\,\, - \,\,0\,\,)}^2}}$

$= \,\,\,\sqrt {\,\,9\,\, + \,\,16\,\, + \,\,9}$

$= \,\,\,\sqrt {\,\,34}$ 

$A$  और  $B$ के निर्देशांक $\left( {\,\,0\,\,,\,\,0\,\,,\,\,6\,} \right)$ और  \[\left( {\,\,0,4,0\,\,} \right)\] है |

${\text{A}}\,\,{\text{B}}$ का मध्य बिन्दु $\left( {\,\,\dfrac{{0 + 0}}{2}\,\,,\,\,\dfrac{{0 + 4}}{2}\,\,,\,\,\dfrac{{6 + 0}}{2}\,\,} \right)$ है 

त्रिभुज $A\,\,B\,\,C$ के माध्यिका $C\,\,F$ की लंबाई 

$= \,\,\,\sqrt {\,\,{{(\,\,6\,\, - \,\,0\,\,)}^2}\,\, + \,\,{{(\,\,0\,\, - \,\,2\,\,)}^2}\,\, + \,\,{{(\,\,0\,\, - \,3\,\,)}^2}}$

$= \,\,\,\sqrt {\,\,36\,\, + \,\,4\,\, + \,\,9}$

$= \,\,\,\sqrt {\,\,49}$

$= \,\,\,7 $ 

3. यदि त्रिभुज का केंद्रक मूल बिंदु है और शीर्ष \[\mathbf{P\,\,\left( {2{\text{ }}a,{\text{ }}2,6} \right)}\] \[\mathbf{,\,Q\left( { - 4,3{\text{ }}B - 10} \right)}\] और \[\mathbf{R\left( {8,14,2{\text{ }}c} \right)\]हैं \[a,{\text{ }}b}\] तो और $c$ का मान ज्ञात कीजिए।

उत्तर:  त्रिभुज $P\,Q\,R$ के शीर्षों \[P\,\,(\,\,2{\text{ }}a\,\,,{\text{ }}2\,\,,\,\,6\,\,)\,\,,{\text{ }}Q\,\,(\,\, - \,\,4\,\,,\,\,3{\text{ }}b,\,\, - 10\,\,)\,\,,{\text{ }}R\,\,(\,\,8\,\,,\,\,14\,\,,\,\,2{\text{ }}c\,\,)\] 

$\Delta \,\,P\,\,Q\,\,R$ का केन्द्रक  $\left( {\,\,\dfrac{{{x_1}\,\, + \,\,{x_2}\,\, + \,\,{x_3}}}{3}\,\,,\,\,\dfrac{{{y_1}\,\, + \,\,{y_2}\,\, + \,\,{y_3}}}{3}\,\,,\,\,\dfrac{{{z_1}\,\, + \,\,{z_2}\,\, + \,\,{z_3}}}{3}\,\,} \right)$

4. $y$ अक्ष पर उस बिंदु के निर्देशांक ज्ञात कीजिए जिसकी बिंदु \[\mathbf{P\,\,\left( {\,3\,, - 2\,,\,5\,} \right)}\]से दूर $\mathbf{5\,\sqrt {\,2} }$ है।

उत्तर:  $y\,\, - $अक्ष पर किसी बिंदु के निर्देशांक $A\,\,\left( {\,\,0\,\,,\,\,{y_1}\,\,,\,\,0\,\,} \right)$  है। $A$ से \[P\,\,\left( {\,\,3\,\,,\,\, - 2\,\,,\,\,5\,\,} \right)\]के बीच की दूरी $ = \,\,\,5\,\,\sqrt {\,\,2} $

$A{P^2}\,\, = \,\,{(\,\,3 - 0\,\,)^2}\,\, + \,\,{\left( {\,\, - 2 - {y_1}\,} \right)^2} + \,\,\,{(\,\,5 - 0\,\,)^2} $

$= \,\,9 + {\left( {\,\, - 2 - {y_1}\,\,} \right)^2} + \,\,25 $

$= \,\,{\left( {\,\,{y_1}\,\, + \,\,2\,\,} \right)^2}\,\, + \,\,34 $ 

$AP\,\, = \,\,\sqrt {\,{{\left( {\,\,{y_1} + 2\,\,} \right)}^2}\,\, + \,\,34}  = 5\,\,\sqrt {\,\,2}$

$\therefore \,\,\,\,{\left( {\,{y_1} + 2\,} \right)^2} + 34\,\, = \,\,50 $

${\left( {\,\,{y_1} + 2\,\,} \right)^2}\,\, = \,\,50 - 34\,\, = \,\,16 $

${y_1} + 2\,\,\, = \,\,\, \pm 4 $ 

$ + \,\,v\,\,e$  चिन्ह लेने पर  ${y_1}\,\,\, = \,\,4\,\, - \,\,2\,\,\,\,\,\, = \,\,2$

$ - \,\,v\,\,e$  चिन्ह लेने पर  ${y_1}\,\,\, = \,\, - \,\,4\,\, - \,\,2\,\,\,\,\,\, = \,\, - \,\,6$

$y$ अक्ष पर अभीष्ट बिन्दु $\left( {\,\,0\,\,,\,\,2\,\,,\,\,0\,\,} \right)$ और $\left( {\,\,0\,\,,\,\, - \,\,6\,\,,\,\,0\,\,} \right)$ है |

5. \[P\left( {2, - 3,4} \right)\] और \[Q\,\,\left( {\,8,0,10\,} \right)\]को मिलाने वाली रेखा खंड पर स्थित एक बिंदु $R$ को $x$ निर्देशांक $4$  है। बिंदु $R$ के निर्देशांक ज्ञात काजिए | (संकेत मान लीजिए को \[k:{\text{ }}1\] में विभाजित करता है। बिंदु $R$ के निर्देशांक $\left( {\,\dfrac{{8k + 1}}{{k + 1}}\,\,,\,\,\dfrac{{ - 3}}{{k + 1}}\,\,,\,\,\dfrac{{10k + 4}}{{k + 1}}\,} \right)$ है ।)

उत्तर: माना $R\,\,,\,\,P\,\,,\,\,Q$ बिन्दु को $k\,\,:\,\,1$ में विभाजित करता है जबकि $P$ और $Q$ के निर्देशांक $P\,\,(\,\,2\,\,, - 3\,\,,\,\,4\,\,)$ और $Q\,\,(\,\,8\,\,,\,\,0\,\,,\,\,10\,\,)$ है |

बिन्दु $R$ के बिन्दु के निर्देशांक $\left( {\,\,\dfrac{{8\,\,k + 2}}{{k + 1}}\,\,\,,\,\,\,\dfrac{{ - 3}}{{\,\,k + 1}}\,\,\,,\,\,\dfrac{{10\,\,k + 4}}{{k + 1}}\,\,} \right)$

परंतु $x$ बिन्दु के निर्देशांक $4$ के समान है |

$\dfrac{{8k + 2}}{{k + 1}}\,\,\,\, = \,\,4\,\,\,\,\,\,\, \Rightarrow \,\,\,8\,\,k\,\, + \,\,2\,\,\,\,\, = \,\,4\,\,k\,\, + \,\,4 $

$4\,\,k\,\, = \,\,2\,\,\,\,\,\,\,\,\,\, \Rightarrow \,\,k\,\, = \,\,\dfrac{2}{4}\,\,\,\,\,\, \Rightarrow \,\,\,\,k = \dfrac{1}{2}\,\,\,\,\,\,\, = \,\,1\,\,:\,\,2 $ 

$y\,\, - $ निर्देशांक $\dfrac{{ - 3}}{{k + 1}}\,\,\,\,\, = \,\,\dfrac{{ - 3}}{{\dfrac{1}{2} + 1}}\,\,\,\,\, = \,\,\,\dfrac{{ - 3 \times 2}}{3}\,\,\,\,\,\, = \,\,\dfrac{{ - 6}}{3}\,\,\,\,\,\,\, = \,\, - 2$

$z\,\, - $ निर्देशांक  $ = \,\,\dfrac{{10k + 4}}{{k + 1}}\,\,\,\,\,\,\, = \,\,\,\dfrac{{10 \times \dfrac{1}{2} + 4}}{{\dfrac{1}{2} + 1}}\,\,\,\,\,\,\,\, = \,\,\,\dfrac{{5 + 4}}{{\dfrac{3}{3}}}\,\,\,\,\,\,\, = \,\,\dfrac{{9 \times 2}}{3}\,\,\,\,\,\, = \,\,\,\dfrac{{18}}{3}\,\,\,\,\,\,\,\,\, = \,\,\,6$

अत:  $R$ के निर्देशांक  $\left( {\,\,4\,\,,\,\, - 2\,\,,\,\,6\,\,} \right)$ है |

6. यदि बिंदु $A$और $B$ क्रमश: \[\mathbf{\left( {3,4,5} \right)}\] तथा \[\mathbf{\left( { - 1,3, - 7} \right)}\]  हैं। चर बिंदु $P$  द्वारा निर्मित समुच्चय से संबिधत समीकरण ज्ञात कीजिए, जहाँ $\mathbf{P{A^2}\,\, + \,\,P{B^2}\,\, = \,\,{k^2}}$ अचर है।

उत्तर:  माना बिन्दु ${\text{P}}$ के निर्देशांक $\left( {\,\,x\,\,,\,\,y\,\,,\,\,z\,\,} \right)$

बिन्दु $A\,\,\left( {\,\,3\,\,,\,\,4\,\,,\,\,5\,\,} \right)$ 

$P{A^2}\,\, = \,\,{(x - 3)^2} + {(y - 4)^2} + {(z - 5)^2}$

बिन्दु $B\,\,\left( {\,\, - \,\,1\,\,,\,\,3\,\,,\,\,7\,\,} \right)$

$P{B^2}\,\, = \,\,{(x + 1)^2} + {(y - 3)^2} + {(z + 7)^2}$

दिया है 

$P{A^2} + P{B^2} = {k^2} $

$\left[ {\,\,{{(x - 3)}^2} + {{(y - 4)}^2} + {{(z - 5)}^2}\,\,} \right]\,\,\, + \,\,\,\left[ {\,\,{{(x + 1)}^2} + {{(y - 3)}^2} + } \right.\left. {{{(z + 7)}^2}\,\,} \right]\,\, = \,\,{k^2} $

$\Rightarrow \,\,\,\,\left( {\,\,{x^2} + {y^2} + {z^2} - 6x - \,8y - 10z + 9 + 16 + 25\,\,} \right)\,\, + \,\,\left( {\,\,{x^2} + {y^2} + {z^2} + 2x - 6y + 14z + 1 + 9 + 49\,\,} \right)\,\, = \,\,{k^2} $

$\Rightarrow \,\,\,\,\,2\,\,\left( {\,\,{x^2} + {y^2} + {z^2}\,\,} \right)\,\, - \,\,4x - 14y + 4z + 50 + 59 - {k^2}\,\, = \,\,0 $

$\Rightarrow \,\,\,\,2\,\,\left( {\,\,{x^2} + {y^2} + {z^2}\,\,} \right)\,\, - \,\,4x - 14y + 4z + 109 - {k^2}\,\, = \,\,0 $

$\Rightarrow \,\,\,\,\,\,2\,\,\left( {\,\,{x^2} + {y^2} + {z^2}\,\,} \right)\,\, - \,\,4x - 14y + 4z = {k^2} - 109 $

$\Rightarrow \,\,\,\,{x^2} + {y^2} + {z^2} - 2x - 7y + 2z\,\,\,\, = \,\,\,\,\dfrac{{{k^2} - 109}}{2} $ 

NCERT Solutions for Class 11 Maths Chapter 12 Introduction to Three Dimensional Geometry in Hindi

Chapter-wise NCERT Solutions are provided everywhere on the internet with an aim to help the students to gain a comprehensive understanding. Class 11 Maths chapter 12 solution Hindi mediums are created by our in-house experts keeping the understanding ability of all types of candidates in mind. NCERT textbooks and solutions are built to give a strong foundation to every concept. These NCERT Solutions for Class 11 Maths chapter 12 in Hindi ensure a smooth understanding of all the concepts including the advanced concepts covered in the textbook.

NCERT Solutions for Class 11 Maths chapter 12 in Hindi medium PDF download are easily available on our official website (vedantu.com). Upon visiting the website, you have to register on the website with your phone number and email address. Then you will be able to download all the study materials of your preference in a click. You can also download the Class 11 Maths Introduction to Three Dimensional Geometry solution Hindi medium from Vedantu app as well by following the similar procedures, but you have to download the app from Google play store before doing that.

NCERT Solutions in Hindi medium have been created keeping those students in mind who are studying in a Hindi medium school. These NCERT Solutions for Class 11 Maths Introduction to Three Dimensional Geometry in Hindi medium pdf download have innumerable benefits as these are created in simple and easy-to-understand language. The best feature of these solutions is a free download option. Students of Class 11 can download these solutions at any time as per their convenience for self-study purpose.

These solutions are nothing but a compilation of all the answers to the questions of the textbook exercises. The answers/ solutions are given in a stepwise format and very well researched by the subject matter experts who have relevant experience in this field. Relevant diagrams, graphs, illustrations are provided along with the answers wherever required. In nutshell, NCERT Solutions for Class 11 Maths in Hindi come really handy in exam preparation and quick revision as well prior to the final examinations.