Question

Apple falling from a tree, car moving on a straight road, coins moving over a carrom board, giant wheel. Find the odd one out: A. giant wheel B. apple falling from tree C. car moving on a straight road D. coins moving over a carrom board

Answer 1

Hint:To solve this problem, we have to understand the concept of dot product and apply it to the work done in these individual cases to understand if the work is done in these cases or not. In this way, we can find out in which cases, work is actually done and in which cases, work is not done.

Complete step-by-step answer:
Let us understand the definition of the work.
Work is defined as the product of force and displacement.
$W = F \times s$
where F is the force and S is the displacement.
This is the most fundamental definition but, however, the product of force and displacement cannot be done directly, since they are vector quantities and they cannot be operated like how we operate scalar quantities.
The work is thus, a vector product of force and displacement.
There are two kinds of vector products, namely – 1. Dot Product 2. Cross Product
The dot product of two vectors is defined as the product of magnitudes of the vectors and the cosine of the angle between the direction of these vectors. The product is scalar in nature.
If $\overrightarrow a $ and $\overrightarrow b $ are two vectors, their dot product is equal to :
$\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|\left| {\overrightarrow b } \right|\cos \theta $
where $\theta $ is the angle of inclination between the two vectors.
The maximum value of the work is when $\cos \theta = 1 \Rightarrow \theta = {0^ \circ }$ Also, the work done is zero when $\cos \theta = 0 \Rightarrow \theta = {90^ \circ }$
Let us determine the work done in the following cases:
Case 1: Giant wheel
Here, the force acting on any particle of the giant wheel is the centripetal force. This centripetal force is perpendicular to the direction of the displacement vector, which acts tangential to every part of the circle.

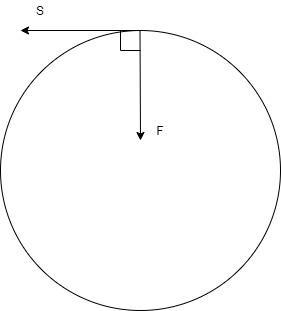
Hence, the inclination between the vectors, $\theta = {90^ \circ }$
Thus, work done is zero since $\cos \theta = \cos {90^ \circ } = 0$
Case 2: Apple falling from a tree
Here, there is gravitational force acting on the apple and the apple falls in the linear straight path which is the same as that of the gravitational force.
Hence, the inclination between the vectors, $\theta = {0^ \circ }$
Thus, work done is maximum since $\cos \theta = \cos {0^ \circ } = 1$
Case 3: Car moving on a straight road
In this case, the movement of the car is along the same direction as that of the acceleration, which in turn is the same direction that the force is applied to the car to move.
Hence, the inclination between the vectors, $\theta = {0^ \circ }$
Thus, work done is maximum since $\cos \theta = \cos {0^ \circ } = 1$
Case 4: Coins moving over a carrom board
When the coins are moved by the striker of the carrom, the coins move in the same line that the striker hits, thus, imparting its force along the same direction as that of the motion.
Hence, the inclination between the vectors, $\theta = {0^ \circ }$
Thus, work done is maximum since $\cos \theta = \cos {0^ \circ } = 1$

So, we can see that only in Case 1, there is zero work done and in the rest of the cases, the work done is maximum.

Hence, the correct option is Option A.

Note:The other vector product, mentioned here, the cross product is defined as follows:
The cross product of two vectors is defined as the product of magnitudes of the vectors and the sine of the angle between the direction of these vectors. The product is a vector whose direction is perpendicular to the plane containing the two vectors.
If $\overrightarrow a $ and $\overrightarrow b $ are two vectors, their cross product is equal to :
$\overrightarrow a \times \overrightarrow b = \left| {\overrightarrow a } \right|\left| {\overrightarrow b } \right|\sin \theta \widehat n$