Question

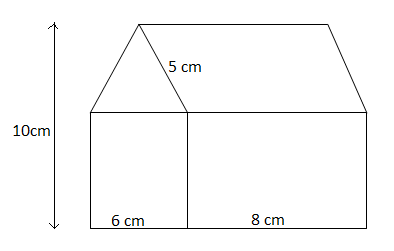
Find the area of the house drawing given in the figure.

Answer 1

Hint:
Here, we have to use the basic formulas of area to find out the total area of the given house. So firstly we have to find out the area of the triangle and then the area of the square below it and then the area of the rectangle and then area of the parallelogram. Summation of all the areas will give the total area of the given house.

Complete step by step solution:
Firstly we will calculate the area of the triangle.
It is given that two sides of the triangle are of length 5cm and the third side is of length 6cm.
Area of triangle \[ = \dfrac{1}{2} \times {\rm{Base}} \times {\rm{Height}}\] where, base is equal to 6cm and height we have to calculate.
So when we draw a perpendicular on the base it will divide it into two parts each of 3cm length. So by applying Pythagoras theorem we will get the height of the triangle. Therefore,
Height of the triangle\[{\rm{ = }}\sqrt {{5^2} - {3^2}} = \sqrt {25 - 9} = \sqrt {16} = 4{\rm{cm}}\]
Therefore, area of triangle \[{\rm{ = }}\dfrac{1}{2} \times 6 \times {\rm{4 = 12 c}}{{\rm{m}}^2}\]
It is given that the total height of the house is 10cm and we found that the height of the triangle is 4cm. So by subtracting the height of the triangle from the total height of the house, we will get the remaining height of the lower portion of the house.
Height of the lower portion of the house \[{\rm{ = 10}} - 4 = 6{\rm{ cm}}\]
Now we will find the area of the square below the triangle.
Area of the square \[{\rm{ = sid}}{{\rm{e}}^2}\] where, side is equal to 6 cm
Therefore, area of the square \[ = 6 \times 6{\rm{ = 36 c}}{{\rm{m}}^2}\]
Now we will calculate the area of the rectangle which is to the right of the square.
Area of the rectangle \[ = {\rm{Base}} \times {\rm{Height}}\] where, base is equal to 8cm and height is equal to 6cm as height of the rectangle is equal to the remaining height of the house.
Therefore, area of the rectangle \[ = 8 \times 6{\rm{ = 48 c}}{{\rm{m}}^2}\]
Now we will calculate the area of the parallelogram.
Area of the parallelogram \[ = {\rm{Base}} \times {\rm{Height}}\] where, base is equal to 8cm and height is equal to 4cm as height of the triangle is equal to the perpendicular height of the parallelogram.
Therefore, area of the parallelogram \[ = 8 \times 4{\rm{ = 32 c}}{{\rm{m}}^2}\]
Now by adding all the areas we will get the value of the total area of the house given in the figure.
Therefore, total area of the house \[{\rm{ = 12 + 36 + 48 + 32 = 128 c}}{{\rm{m}}^2}\]

Hence, \[{\rm{128 c}}{{\rm{m}}^2}\] is the total area of the house.

Note:
Pythagoras theorem stated that in a right angled triangle the square of the long side is equal to the sum of the squares of the other two sides.
Square is a shape which has all its four sides equal in length and has right angles. Rectangle is a shape which has opposite sides equal to each other and has right angles. Parallelogram is similar to the rectangle but it does not have right angles.
Perimeter is the total length of the outer boundary of a shape in two dimensional. Perimeter is measured in meters. Area is the amount of surface covered by a shape in two dimensional. Surface area is the sum of all the areas of the faces of an object or shape. Area and surface area is measured in square meters. Volume is the amount of space occupied by an object in three-dimensional space. Volume is measured in cubic meters.