Question

Find the side and perimeter of a square whose diagonal is 10 cm.

Answer 1

Hint- Use the Pythagoras Theorem in any of the triangles formed from the diagonal of the square, since all sides are equal we will have only one variable, find that and that will be our side. Now calculate the perimeter.

Complete step-by-step answer:

We will use the following figure to solve the problem.

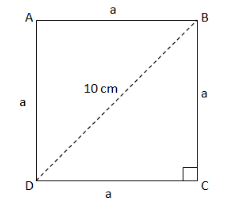
Given that diagonal of square = 10 cm.
In the figure BD = 10 cm.
Let the sides of the square be “a” cm as mentioned in the figure.
We know that each side of the square is equal and each angle is right angled.
Let us take a triangle from the figure in order to find the side.
In right angled $\Delta BCD$
$BC = \left( a \right)cm,CD = \left( a \right)cm\& BD = 10cm$
Let us use Pythagoras theorem for right angled triangle BCD.
According to Pythagoras theorem, for right angled triangle:
${\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{Sid}}{{\text{e}}_1}} \right)^2} + {\left( {{\text{Sid}}{{\text{e}}_2}} \right)^2}$
Using the same for the given triangle BCD we get:
$ \Rightarrow {\left( {BD} \right)^2} = {\left( {BC} \right)^2} + {\left( {CD} \right)^2}$
Substituting the value in the equation we get:
$
   \Rightarrow {\left( {10} \right)^2} = {\left( a \right)^2} + {\left( a \right)^2} \\
   \Rightarrow 100 = 2{\left( a \right)^2} \\
   \Rightarrow {\left( a \right)^2} = \dfrac{{100}}{2} = 50 \\
   \Rightarrow a = \sqrt {50} \\
   \Rightarrow a = 5\sqrt 2 cm \\
 $
Now as we have the side of the square, we can easily find the perimeter.
Perimeter of the square is equal to $4 \times \left( {{\text{side}}} \right)$
So, Perimeter:
$
   = 4 \times \left( {5\sqrt 2 cm} \right) \\
   = 20\sqrt 2 cm \\
 $
Hence, the side of the square is $5\sqrt 2 cm$ and the perimeter of the square is $20\sqrt 2 cm$ .

Note- A diagonal is a line segment joining two vertices of a polygon or polyhedron, when those vertices are not on the same edge. Pythagoras theorem gives the relation between the sides of a right angled triangle. Perimeter of the square can also be found directly from the diagonal by the use of formula: $P = 2\sqrt 2 d$ . But the method used here is the basic one.