Vedantu's Class 10 Conic Sections Exercise 10.2 Solutions
NCERT Solutions for Class 10 Maths Chapter 10 Conic Sections Exercise 10.2
FAQs on NCERT Solutions for Class 10 Maths Chapter 10 Conic Sections Exercise 10.2
1. Where can I download the stepwise NCERT Solutions for Class 11 Maths Chapter 10 Conic Sections in PDF format?
You can download the stepwise NCERT Solutions for Class 11 Maths Chapter 10 Conic Sections in PDF format from Vedantu's NCERT Solutions section. All solutions are arranged exercise-wise and strictly follow the CBSE 2025–26 NCERT textbook pattern, ensuring every answer matches the official answer format asked in exams.
2. Are the NCERT Solutions for Class 11 Maths Chapter 10 available for both English and Hindi medium students?
Yes, NCERT Solutions for Class 11 Maths Chapter 10 are available in both English and Hindi medium. These solutions align with the latest CBSE guidelines and use NCERT-approved terminology for both language mediums, providing correct explanations for all exercises and intext questions.
3. How can I access correct and complete answers to the Miscellaneous Exercise of Chapter 10 for Class 11 Maths?
You can access the correct and complete answers to the Miscellaneous Exercise of Chapter 10 for Class 11 Maths on Vedantu in the NCERT Solutions section. Every question includes a stepwise explanation that follows the NCERT pattern, helping you understand the reasoning behind each solution, just as required by CBSE 2025–26.
4. Do the NCERT solutions for Class 11 Maths Chapter 10 cover all exercises like 10.1, 10.2, and 10.3?
Yes, the NCERT Solutions for Class 11 Maths Chapter 10 cover every exercise, including Ex 10.1, Ex 10.2, Ex 10.3, and the Miscellaneous Exercise. Each solution is prepared according to the NCERT answer key and provides detailed, stepwise methods as per CBSE-approved guidelines.
5. What is the official CBSE answer format for solving straight lines questions in Class 11 Chapter 10?
The official CBSE answer format for straight lines questions in Class 11 Chapter 10 requires using proper formulas as per NCERT guidelines, writing each calculation step clearly, and providing explanations for slope, intercepts, and points when required. All Vedantu NCERT Solutions present answers in this CBSE-prescribed format for maximum marks.
6. Can I find NCERT Solutions for both Conic Sections and Straight Lines in Chapter 10 of Class 11 Maths?
Yes, Class 11 Maths Chapter 10 in NCERT covers both Conic Sections and Straight Lines. All solutions, including stepwise working for each topic, are included in Vedantu's NCERT Solutions, fully updated as per the CBSE 2025–26 syllabus.
7. How do the stepwise NCERT Solutions help me prepare for the CBSE board exam?
The stepwise NCERT Solutions explain every answer clearly, mirroring the marking scheme of CBSE board exams. Each step is justified according to the NCERT answer key, allowing you to learn proper presentation and ensuring you don’t miss marks for skipped calculations or reasoning.
8. Are these NCERT Solutions for Class 11 Maths Chapter 10 regularly updated to match the latest CBSE syllabus?
Yes, all NCERT Solutions for Class 11 Maths Chapter 10 on Vedantu are updated every academic year to reflect changes in the CBSE syllabus and NCERT textbook. This ensures you always have access to the correct and current answers for your board preparation.
9. Is Class 11 Maths Chapter 10 considered one of the most difficult chapters?
Class 11 Maths Chapter 10 (Conic Sections and Straight Lines) is often considered challenging due to its advanced coordinate geometry concepts. Practicing with detailed NCERT Solutions can simplify the understanding and help you solve CBSE questions accurately as per the textbook method.
10. How should I approach solving questions involving straight lines in Exercise 10.2 and 10.3?
When solving straight lines questions in Exercise 10.2 and 10.3, begin by identifying the known values (slope, intercepts, points), use the correct formula (e.g., y = mx + c, or x/a + y/b = 1), and show each calculation step as per the NCERT answer format. The Vedantu solutions give a stepwise breakdown for all such questions in line with CBSE requirements.
11. Can I use these NCERT Solutions for quick revision before my final exam?
Yes, these NCERT Solutions are ideal for quick revision before your final exam, as they provide concise, stepwise answers reflecting the exact NCERT answer key and help you review all key types of questions expected in the CBSE board exam.
12. What is a common mistake students make while solving Conic Sections questions using NCERT Solutions?
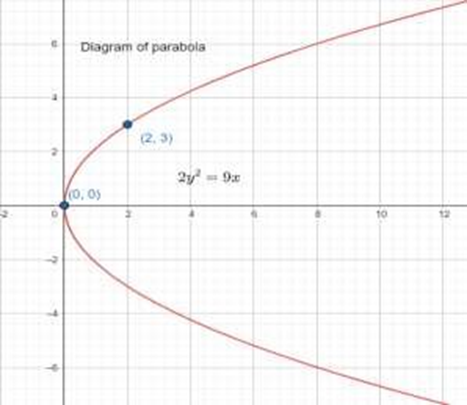
A common mistake is skipping intermediate steps or not mentioning the standard form of equations for a parabola, ellipse, or hyperbola. Always follow the NCERT answer format by starting with standard equations, substituting values precisely, and simplifying each step to get full marks as per CBSE guidelines.




















 Watch Video
Watch Video