Watch Video
NCERT Solutions for Class 10 Maths Chapter 10 Circles in Hindi PDF Download
Well offered by the leading e-learning platform Vedantu. If you are a student of Class 10, you have reached the right platform. The NCERT Solutions for Class 10 Maths in Hindi provided by us are designed in a simple, straightforward language, which are easy to memorise.
- 2.1प्रश्नावली 10.1
- 2.2प्रश्नावली 10.2
You will also be able to download the PDF file for NCERT Solutions for Class 10 Maths in English and Hindi from our website at absolutely free of cost. Download NCERT Solutions for Class 10 Maths from Vedantu, which are curated by master teachers.
NCERT, which stands for The National Council of Educational Research and Training, is responsible for designing and publishing textbooks for all the classes and subjects. NCERT textbooks covered all the topics and are applicable to the Central Board of Secondary Education (CBSE) and various state boards.
We, at Vedantu, offer free NCERT Solutions in English medium and Hindi medium for all the classes as well. Created by subject matter experts, these NCERT Solutions in Hindi are very helpful to the students of all classes.
NCERT Solutions for Class 10 Maths Chapter 10 - In Hindi
ShareShareप्रश्नावली 10.1
1. एक वृत्त की कितनी स्पर्श रेखाएँ हो सकती हें?
उत्तर: एक वृत्त में अनंत संख्या में स्पर्श रेखाएं हो सकती हैं।
2. रिक्त स्थानों पूर्ति कीजिए:
(i) किसी वृत्त की स्पर्श रेखा उसे___________ बिंदुओ पर प्रतिच्छेदकरती हे।
(ii) वृत्त को दो बिंदुओ पर प्रतिच्छेद करने वाली रेखा को___________कहतेहैं।
(iii) एक वृत्त की ___________ समांतर स्पर्श रेखाएँ हो सकती हें।
(iv) वृत्त तथा उसकी स्पर्श रेखा के उभयनिष्ठ बिंदु को _____________ कहते हैं।
उत्तर: (i) किसी वृत्त की स्पर्श रेखा उसे एक बिंदुओ पर प्रतिच्छेद करतीहे।
(ii) वृत्त को दो बिंदुओ पर प्रतिच्छेद करने वाली रेखा को छेदक रेखा कहते हैं।
(iii) एक वृत्त की दो समान्तर स्पर्श रेखाएँ हो सकती हें।
(iv) वृत्त तथा उसकी स्पर्श रेखा के उभयनिष्ठ बिंदु को स्पर्श बिंदु कहतेहैं।
3. \[\mathbf{5}\] सेमी त्रिज्या वाले एक वृत्त के बिंदु P पर स्पर्श रेखा PQ केंद्रO से जाने वाली एक रेखा से बिंदु Q पर इस प्रकार मिलती है कि \[\mathbf{OQ} = \mathbf{12}\] सेमी। PQ की लम्बाई है:
(A) \[\mathbf{2}\] सेमी
(B) \[\mathbf{13}\] सेमी
(C) \[\mathbf{8}.\mathbf{5}\] सेमी
(D) \[\surd \mathbf{119}\] सेमी
उत्तर: (D) \[\surd \text{119}\] सेमी
4. एक वृत्त खींचिए और दो एक दी गई रेखा के समांतर दो ऐसी रेखाएँ खींचिए कि उनमें से एक स्पर्श रेखा हो तथा दूसरी छेदक रेखा हो।
उत्तर:
प्रश्नावली 10.2
संख्या 1,2,3, में सही विकल्प चुनिए एवं उचित कारण दीजिए
1. एक बिंदु Q से एक वृत पर स्पर्श रेखा की लम्बाई \[\mathbf{24}\text{ }\mathbf{cm}\] तथा Q की केंद्र से दूरी 25 cm है I वृत की त्रिज्या है :
(A) \[\mathbf{7}\text{ }\mathbf{cm}\]
(B) \[\mathbf{12}\text{ }\mathbf{cm}\]
(C) \[\mathbf{15}\text{ }\mathbf{cm}\]
(D) \[\mathbf{24}.\mathbf{5}\text{ }\mathbf{cm}\]
उत्तर:
\[\text{OP } = ?\]
\[\text{OQ } = \text{ 24 cm}, \text{ PQ }= \text{ 25 cm}\]
चूँकि \[\text{OP}\bot \text{PQ}\] है, पैथागोरस प्रमेय से -
\[\text{P}{{\text{Q}}^{\text{2}}}=\text{O}{{\text{P}}^{\text{2}}}+\text{O}{{\text{Q}}^{\text{2}}}\].
\[\text{2}{{\text{5}}^{\text{2}}}=\text{O}{{\text{P}}^{\text{2}}}+\text{2}{{\text{4}}^{\text{2}}}\]
\[\text{O}{{\text{P}}^{\text{2}}} = \text{ 625 }\text{ 576}\]
\[\text{O}{{\text{P}}^{\text{2}}} = \text{ 49}\]
\[\text{OP } = \surd \text{49}\]
\[\text{OP} = \text{ 7 cm}\]
(A) \[\text{7 cm}\]
2 .आकृति 10.11 में, यदि TP केंद्रO वाले किसी वृत्त पर दो स्पर्श रेखाएँ इस प्रकार है की \[\angle \mathbf{POQ}\text{ } = \text{ }\mathbf{11}{{\mathbf{0}}^{\mathbf{o}}}\], तो \[\angle \mathbf{PTQ}\] बराबर है :
(A)\[\mathbf{6}{{\mathbf{0}}^{\mathbf{o}}}\]
(B) \[\mathbf{7}{{\mathbf{0}}^{\mathbf{o}}}\]
(C) \[\mathbf{8}{{\mathbf{0}}^{\mathbf{o}}}\]
(D) \[\mathbf{9}{{\mathbf{0}}^{\mathbf{o}}}\]
उत्तर: \[\angle \text{POQ } + \angle \text{PTQ } = \text{18}{{0}^{o}}\]
\[\text{11}{{0}^{o}}\text{ } + \angle \text{PTQ } = \text{18}{{0}^{o}}\]
\[\angle \text{PTQ } = \text{18}{{0}^{o}}-\text{11}{{0}^{o}}\]
\[\angle \text{PTQ } = {{70}^{o}}\]
\[\left( \text{B} \right)\text{ 7}0{}^\circ \]
3.यदि एक बिंदु P से O केंद्र वाले किसी वृत्त पर PA, PB स्पर्श रेखाएँ \[\mathbf{8}{{\mathbf{0}}^{\mathbf{o}}}\] के कोण पर झुकी हों, तो \[\angle \mathbf{POA}\] बराबर है:
(A) \[\mathbf{5}{{\mathbf{0}}^{\mathbf{o}}}\]
(B) \[\mathbf{6}{{\mathbf{0}}^{\mathbf{o}}}\]
(C) \[\mathbf{7}{{\mathbf{0}}^{\mathbf{o}}}\]
(D) \[\mathbf{8}{{\mathbf{0}}^{\mathbf{o}}}\]
उत्तर:
\[\angle APB\text{ } = {{80}^{o}}\]
\[\angle APB\text{ } = {{80}^{o}}\dfrac 2 = {{40}^{o}}\]
स्पर्श बिंदु पर \[\angle A = {{90}^{o}}\]
त्रिभुज AOP में,
\[\angle \text{A } + \text{ }\angle \text{APO } + \text{ }\angle \text{POA } = {{180}^{o}}\]
\[{{90}^{o}}\text{ } + \text{ 4}{{0}^{o}}\text{ } + \text{ }\angle \text{POA } = {{180}^{o}}\]
\[\angle \text{POA } = {{180}^{o}}-{{130}^{o}}\]
\[\angle \text{POA } = {{50}^{o}}\]
(A) \[{{50}^{o}}\]
4 .सिद्ध कीजिए वृत किसी वृत्त के किसी व्यास के सिरों पर खींची गई स्पर्श रेखाएँ समांतर होती हैI
उत्तर:
O केंद्र वाले वृत्त की दो स्पर्श रेखाएँ AB तथा CD हैं जो वृत्त को X तथा Y पर क्रमशः स्पर्श करती है I [दिया गया है]
सिद्ध करना है : \[\text{AB }||\text{ CD}\]
\[\text{OX}\bot \text{AB}\]
अत: \[\angle BXO\text{ } = {{90}^{o}}\]…….. (i)
इसी प्रकार, \[\text{OY}\bot \text{CD}\]
अत: \[\angle DYO\text{ } = {{90}^{o}}\]…….. (i)
समीकरण(i) तथा(ii) जोड़ने पर
\[\angle \text{BXO } + \angle \text{DYO } = {{90}^{o}} + {{90}^{o}}\]
\[ = >\angle \text{BXO } + \angle \text{DYO } = {{180}^{o}}\]
चूँकि एक ही ओर से अंत:आसन्न कोण संपूरक हैं, इसलिए
∴\[\text{AB }||\text{ CD}\]
5 .सिद्ध कीजिए की स्पर्श बिंदु से स्पर्श रेखा पर खींचा गया लंब वृत्त के केंद्र से होकर जाता है I
उत्तर:
मना O केंद्र वाले वृत्त पर AB एक स्पर्श रेखा है जो वृत्त को P पर स्पर्श करती है I
मान लीजिये की बिंदु P से स्पर्श रेखा है जो वृत्त के केंद्र से होकर जाता है I यह एक और बिंदु O’ से होकर जाता है I हम इसे विरोधाभास विधि से सिद्ध करेंगे I
\[\angle \text{O}\prime \text{PB} = \text{9}0{}^\circ \]………. (1)
हम जानते है वृत त्रिज्या, स्पर्श रेखा पर लम्बा होती है I
∴ \[\angle \text{OPB} = \text{9}0{}^\circ \]………. (2)
समीकरण(1)और(2) के तुलना करने पर,
\[\angle \text{O}\prime \text{PB } = \angle \text{OPB}\]...........(3)
आकृति में यह सपष्ट होता है की,
\[\angle \text{O}\prime \text{PB }<\angle \text{OPB}\]...........(4)
इसलिए, \[\angle \text{O}\prime \text{PB } = \angle \text{OPB}\] असंभव है I
6.एक बिंदु A से, जो एक वृत्त के केंद्र से \[\mathbf{5cm}\] दूरी पर है, वृत्त पर स्पर्श रेखा की लम्बाई \[\mathbf{4cm}\] हैI वृत्त की त्रिज्या ज्ञात कीजिए I
उत्तर:
समकोण त्रिभुज AOB में, पैथागोरस प्रमेय से
\[\text{O}{{\text{A}}^{\text{2}}} = \text{ O}{{\text{B}}^{\text{2}}} + \text{ A}{{\text{B}}^{\text{2}}}\]
\[{{\text{5}}^{\text{2}}} = \text{ O}{{\text{B}}^{\text{2}}} + \text{ }{{\text{4}}^{\text{2}}}\]
\[\text{O}{{\text{B}}^{\text{2}}} = \text{ }{{\text{5}}^{\text{2}}}\text{ }{{\text{4}}^{\text{2}}}\]
\[\text{O}{{\text{B}}^{\text{2}}} = \text{ 25 }\text{ 16}\]
\[\text{O}{{\text{B}}^{\text{2}}} = \text{ 9}\]
\[\text{OB} = \text{3 cm}\]
7.दो सकेंद्रीय वृत्तों की त्रिज्याएँ \[\mathbf{5cm}\] तथा \[\mathbf{3}\text{ }\mathbf{cm}\] हैI बड़े वृत्त की उस जीवा की लम्बाई ज्ञात कीजिए जो छोटे वृत्त को स्पर्श करती होI
उत्तर:
दो संकेंद्री वृत्त जिसका केंद्र O है और बड़े वृत्त की जीवा AB है जो छोटे वृत्त को बिंदु M पर प्रतिच्छेद करती है I
त्रिज्याएँ क्रमशः \[\text{AO } = \text{ 5 cm}\] और \[\text{OM } = \text{ 3 cm}\] है I \[\text{OM}\bot \text{AB}\] है I
अत: समकोण त्रिभुज AOM में, पाइथागोरस प्रमेय से,
\[\text{O}{{\text{A}}^{\text{2}}} = \text{ O}{{\text{M}}^{\text{2}}} + \text{ A}{{\text{M}}^{\text{2}}}\]
\[{{\text{5}}^{\text{2}}} = \text{ }{{\text{3}}^{\text{2}}} + \text{ A}{{\text{M}}^{\text{2}}}\]
\[{{\text{5}}^{\text{2}}}\text{ }{{\text{3}}^{\text{2}}} = \text{ A}{{\text{M}}^{\text{2}}}\]
\[\text{25 }\text{ 9 } = \text{ A}{{\text{M}}^{\text{2}}}\]
\[\text{A}{{\text{M}}^{\text{2}}} = \text{ 16}\]
\[\text{AM } = \text{ 4 cm}\]
\[\text{AB } = \text{ 2 }\times \text{ AM}\]
\[ = \text{ 2 }\times \text{ 4 } = \text{ 8 cm}\]
8.एक वृत्त के परिगत एक चतुर्भुजABCD खींचा गया है (देखिए आकृति 10.12)| सिद्ध कीजिए : \[\mathbf{AB}\text{ } + \text{ }\mathbf{CD}\text{ } = \text{ }\mathbf{AD}\text{ } + \text{ }\mathbf{BC}\].
आकृति 10.12
उत्तर:
ABCD एक O केंद्र वाले वृत्त के परिगत बना चतुर्भुज है I रेखाएँ AB, BC, CD और AD क्रमशः बिंदु P, Q, R और S पर स्पर्श करती हैं I [दिया गया है ]
सिद्ध करना है वृत, \[\text{AB } + \text{ CD } = \text{ AD } + \text{ BC}\]
P और S स्पर्श बिंदु हैं I
अत: \[\text{AP } = \text{ AS}\] …………… (i) प्रमेय 10.2 से
इसी प्रकार,
\[\text{BP } = \text{ BQ}\] …………… (ii)
\[\text{CR } = \text{ CQ}\] …………… (iii)
और \[\text{DR } = \text{ DS}\] …………… (iv)
समी.(i), (ii), (iii) और (iv) जोड़ने पर
\[\text{AP } + \text{ BP } + \text{ CR } + \text{ DR } = \text{ AS } + \text{ DS } + \text{ BQ } + \text{ CQ}\]
∴\[\text{AB } + \text{ CD } = \text{ AD } + \text{ BC}\]
9.आकृति 10.13 में XY तथा X’Y’, O केंद्र वाले किसी वृत्त पर दो समांतर स्पर्श रेखाएँ हैं और स्पर्श बिंदु C पर स्पर्श रेखा AB, XY को A तथा X’Y’ को B पर प्रतिच्छेद करती है I सिद्ध कीजिए की \[\angle \mathbf{AOB}\text{ } = \text{ }\mathbf{9}{{\mathbf{0}}^{\mathbf{o}}}\] है I
आकृति 10.13
उत्तर:
XY तथा X’Y’, O केंद्र वाले किसी वृत्त पर दो समांतर स्पर्श रेखाएँ हैं और स्पर्श बिंदु C पर स्पर्श रेखा AB, XY को A तथा X’Y’ को B पर प्रतिच्छेद करती है I [दिया गया है ]
सिद्ध करना है वृत, \[\angle AO\text{B} = \text{9}0{}^\circ \]
प्रमाण :
\[\vartriangle AOP\] और \[\vartriangle AOC\] में
\[\text{PA } = \text{ CA}\] (प्रमेय 10.2 से)
\[\angle \text{APO } = \angle \text{ACO } = \text{9}0{}^\circ \]\[(\text{AO } = \text{ AO})\] (उभयनिष्ट कर्ण)
RHS सर्वांगसमता नियम से
\[\vartriangle AOP\cong \vartriangle AOC\]
इसलिए,
\[\angle \text{PAO } = \angle \text{CAO}\].......... (i)by (PCT)
\[\vartriangle BOQ\cong \vartriangle BOC\]
इसलिए, \[\angle \text{QBO } = \angle \text{CBO}\] …….. (ii)by (PCT)
\[\text{XY }||\text{ X}\text{Y}\] दिया है |
इसलिए, \[\angle \text{PAC } + \angle \text{QBC } = 180{}^\circ \] (तिर्यक रेखा के एक ही ओर के अंत: कोणों का योग)
या \[(\angle \text{PAO } + \angle \text{CAO})\text{ } + \text{ }(\angle \text{QBO } + \angle \text{CBO})\text{ } = 180{}^\circ \]
या \[(\angle \text{CAO } + \angle \text{CAO})\text{ } + \text{ }(\angle \text{CBO } + \angle \text{CBO}) = 180{}^\circ \]
समी. (i) तथा (ii) के प्रयोग से
या \[\text{2}\angle \text{CAO } + \text{ 2}\angle \text{CBO } = 180{}^\circ \]
या \[\text{2 }(\angle \text{CAO } + \angle \text{CBO})\text{ } = 180{}^\circ \]
या \[\angle \text{CAO } + \angle \text{CBO } = 90{}^\circ \] ………….. (iii)
त्रिभुज AOB में,
\[\angle \text{AOB } + \angle \text{CAO } + \angle \text{CBO } = 180{}^\circ \]
\[\angle \text{AOB } + 90{}^\circ \text{ } = 180{}^\circ \]
\[\angle \text{AOB } = 180{}^\circ -90{}^\circ \]
∴\[\angle \text{AOB } = 90{}^\circ \]
10.सिद्ध कीजिए वृत किसी बाह्य बिंदु से किसी वृत्त पर खींची गई स्पर्श रेखाओं के बीच का कोण स्पर्श बिंदुओं को मिलाने वाले रेखाखंड द्वारा केंद्र पर अंतरित कोण का संपूरक होता है I
उत्तर:प्रमाण :
चूँकि स्पर्श रेखा से केंद्र को मिलाने वाली रेखाखंड लंब होती है I
\[\text{OA}\bot \text{AP}\] और \[\text{OB}\bot \text{BP}\]
अत: \[\angle OAP\text{ } = 90{}^\circ \]……….. (i)
और \[\angle OBP\text{ } = 90{}^\circ \]……….. (ii)
चूँकि APBO एक चतुर्भुज है इसलिए,
\[\angle \text{OAP } + \angle \text{AOB } + \angle \text{OBP } + \angle \text{APB } = 360{}^\circ \]
\[90{}^\circ \text{ } + \angle \text{AOB } + 90{}^\circ + \angle \text{APB } = 360{}^\circ \]
\[180{}^\circ \text{ } + \angle \text{AOB } + \angle \text{APB } = 360{}^\circ \]
\[\angle \text{AOB } + \angle \text{APB } = 360{}^\circ -180{}^\circ \]
∴\[\angle \text{AOB } + \angle \text{APB } = 180{}^\circ \]
11.सिद्ध कीजिए वृत किसी वृत्त के परिगत समान्तर चतुर्भुज समचतुर्भुज होता है I
उत्तर:ABCD एक O केंद्र वाले वृत्त के पारगत बना समांतर चतुर्भुज है | रेखाएँ AB, BC, CD और AD क्रमशः बिंदु P, Q, R और S पर स्पर्श करती हैं I [दिया गया है]
सिद्ध करना है,ABCD एक समचतुर्भुज है I
प्रमाण: चूँकि ABCD एक समांतर चतुर्भुज है इसलिए
\[\text{AB } = \text{ CD}\] ………… (i) (समांतर चतुर्भुज की सम्मुख भुजा)
\[\text{BC } = \text{ AD}\] ……… (ii)
A, P और S स्पर्श बिंदु हैं I
अत: \[\text{AP } = \text{ AS}\] …………… (iii) प्रमेय 10.2 से
इसी प्रकार,
\[\text{BP } = \text{ BQ}\] …………… (iv)
\[\text{CR } = \text{ CQ}\] …………… (v)
\[\text{DR } = \text{ DS}\] …………… (vi)
समी० (iii), (iv), (v) और(vi) जोड़ने पर,
\[\text{AP } + \text{ BP } + \text{ CR } + \text{ DR } = \text{ AS } + \text{ DS } + \text{ BQ } + \text{ CQ}\]
\[\text{AB } + \text{ CD } = \text{ AD } + \text{ BC}\]
\[\text{AB } + \text{ AB } = \text{ AD } + \text{ AD}\] समी० (i) तथा (ii) से
\[\text{2 AB } = \text{ 2 AD}\]
\[\text{AB } = \text{ AD}\] ……… (vii)
समीकरण (i), (ii) और(vii) से
\[\text{AB } = \text{ BC } = \text{ CD } = \text{ AD}\]
अत: ABCD एक समचतुर्भुज है I
1.4cm त्रिज्या वाले एक वृत्त के परिगत एक त्रिभुज ABC इस प्रकार खींचा गया है की रेखाखंड BD और DC (जिनमे स्पर्श बिंदु D द्वारा BC विभाजित है) की लम्बाई क्रमशः \[\mathbf{8}\text{ }\mathbf{cm}\] और \[\mathbf{6}\text{ }\mathbf{cm}\] हैं (देखिए आकृति 10.14) I भुजाएँAB और AC ज्ञात कीजिएI
आकृति 10.14
उत्तर:माना \[\text{AF } = \text{ AE } = \text{ x cm}\] (प्रमेय 10.2 से)
इसी प्रकार \[\text{CD } = \text{ CE } = \text{ 6 cm}\] और \[\text{BD } = \text{ BF } = \text{ 8 cm}\]
अत: \[\text{AB } = \text{ 8 } + \text{ x cm},\text{ BC } = \text{ 8 } + \text{ 6 } = \text{ 14 cm}\] और \[\text{AC } = \text{ 6 } + \text{ x cm}\]
\[\text{OD } = \text{ OF } = \text{ OE } = \text{ 4 cm}\] (त्रिज्या)
अब त्रिभुज का क्षेत्रफल हेरॉन सूत्र से
\[\text{a } = \text{ 8 } + \text{ x cm},\text{ b } = \text{ 14 cm}\] और \[\text{c } = \text{ 6 } + \text{ x cm}\]
\[\text{s} = \frac{a + b + c}{2} = \frac{\text{8} + x + \text{14} + \text{6} + x}{2} = \frac{\text{28} + \text{2x}}{2} = \frac{\text{2}(\text{14} + x)}{2} = \text{ 14} + \text{x}\]
∆𝐴𝐵𝐶 का क्षेत्रफल = \[\sqrt{s(s-a)(s-b)(s-c)}\]
\[ = \sqrt{(\text{14 } + x)[\text{14 } + x-\text{ }(\text{8 } + x)][\text{14 } + x-\text{ 14}][\text{14 } + x-\text{ }(\text{6 } + x)]}\]
\[ = \sqrt{(\text{14 } + x)[\text{14 } + x-\text{ 8 }-x][x][\text{14 } + x-\text{ 6 }-x]}\]
\[ = \sqrt{(\text{14 } + x)\left[ \text{6} \right][x]\left[ \text{8} \right]}\]
\[ = \sqrt{\text{48 }\times \text{ }(\text{14 } + x)}\]𝑐𝑚2 …….. (i)
∆ABC का क्षेत्रफल \[ = \angle \text{AOB} + \angle \text{BOC} + \angle \text{AOC}\]
\[ = \frac{1}{2}(AB\times OF + BC\times OD + AC\times OE)\]
\[ = \frac{1}{2}(8 + x\times \text{ 4 } + \text{ 14 }\times \text{ 4 } + \text{ 6 } + x\times \text{ 4})\]
\[ = \frac{1}{2}\times \text{ 4}(\text{8 } + x + \text{ 14 } + \text{ 6 } + x)\]
\[ = \text{ 2}\left( \text{28} + \text{2x} \right)\]𝑐𝑚2 …….(ii)
समीकरण (i) और (ii) से चूँकि दोनों त्रिभुज ABC के क्षेत्रफल हैं I
\[\sqrt{\text{48 }\times \text{ }(\text{14 } + x)\text{ } = \text{ 2}\left( \text{28} + \text{2x} \right)}\]
\[\text{48x }\left( \text{14 } + \text{ x} \right)\text{ } = \text{ }{{\left[ \text{2}\left( \text{28 } + \text{ 2x} \right) \right]}^{\text{2}}}\]
\[\text{48x }\left( \text{14 } + \text{ x} \right)\text{ } = \text{ }{{\left[ \text{4}\left( \text{14 } + \text{ x} \right) \right]}^{\text{2}}}\]
\[\text{48x }\left( \text{14 } + \text{ x} \right)\text{ } = \text{ }\left[ \text{4 }\times \text{ 4 }\left( \text{14 } + \text{ x} \right)\text{ }\left( \text{14 } + \text{ x} \right) \right]\]
\[\text{48x } = \text{ 16 }\left( \text{14 } + \text{ x} \right)\]
\[\text{3x } = \text{ }\left( \text{14 } + \text{ x} \right)\] सरल करने पर
\[\text{2x } = \text{ 14}\]
\[\text{x } = \text{ 7}\]
अत: \[\text{AB } = \text{ 8 } + \text{ 7 } = \text{ 15 cm}\] और \[\text{AC } = \text{ 6 } + \text{ 7 } = \text{ 13 cm}\]
12.सिद्ध कीजिए की वृत्त के परिगत बनी चतुर्भुज की आमने – सामने की भुजाएँ केंद्र पर संपूरक कोण अंतरित करती हैं I
उत्तर:
ABCD, O केंद्र वाले एक वृत्त के परिगत बना चतुर्भुज है I
\[\angle AOB + \angle COD = \text{ 18}0{}^\circ \] [सिद्ध करना है]
प्रमाण : \[\vartriangle AOB\cong \vartriangle \text{AOR}\] प्रमेय 10.2 से,
\[\angle \text{1 } = \angle \text{2}\]......(i)
इसी प्रकार,
\[\angle \text{3 } = \angle \text{4}\]......(ii)
\[\angle \text{5 } = \angle \text{6}\]......(iii)
\[\angle \text{7 } = \angle \text{8}\]......(iv)
\[\angle \text{1 } + \angle \text{2 } + \angle \text{3 } + \angle \text{4 } + \angle \text{5 } + \angle \text{6 } + \angle \text{7 } + \angle \text{8 } = \text{ 36}0{}^\circ \]
\[\angle \text{2 } + \angle \text{2 } + \angle \text{3 } + \angle \text{3 } + \angle \text{6 } + \angle \text{6 } + \angle \text{7 } + \angle \text{7 } = \text{ 36}0{}^\circ \]
समीकरण (i), (ii), (iii) और (iv) के प्रयोग से,
\[\text{2}\angle \text{2 } + \text{ 2}\angle \text{3 } + \text{ 2}\angle \text{6 } + \text{ 2}\angle \text{7 } = \text{ 36}0{}^\circ \]
\[\text{2}(\angle \text{2 } + \angle \text{3 } + \angle \text{6 } + \angle \text{7})\text{ } = \text{ 36}0{}^\circ \]
\[\angle \text{2 } + \angle \text{3 } + \angle \text{6 } + \angle \text{7 } = \text{ }\frac{\text{36}0{}^\circ }{2}\]
\[\angle AOB + \angle COD = \text{ 18}0{}^\circ \]
FAQs on NCERT Solutions for Class 10 Maths Chapter 10 - In Hindi
1. Define circle and tangent to a circle in Chapter 10 of Class 10 Maths?
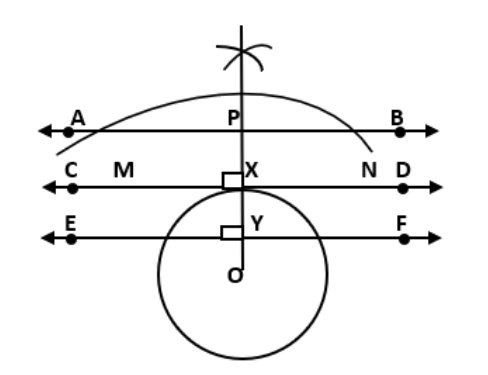
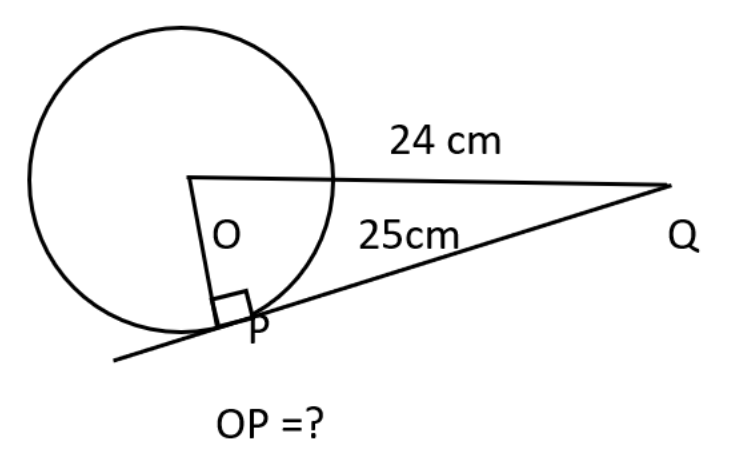
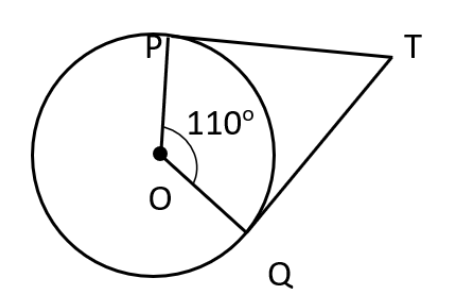
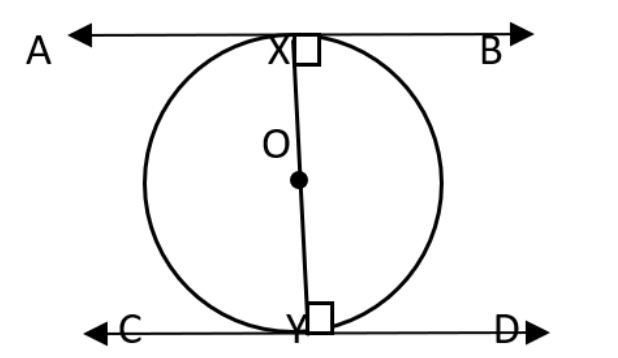
There can be three possibilities of the line with the circle; that the line will be non-intersecting, line touching the circle and the third point is that the line has two common points which means the line cuts the circle. The tangent of a circle is the line that touches the circle at a single point. It has to be noted that for every point on the circle there is a specific tangent.
2. What are points to be noted to draw a tangent of the circle?
The following points are to be noted to draw a tangent of a circle -
We cannot draw any tangent from the point lying inside the circle.
There can be only one tangent drawn from the point lying on the circle.
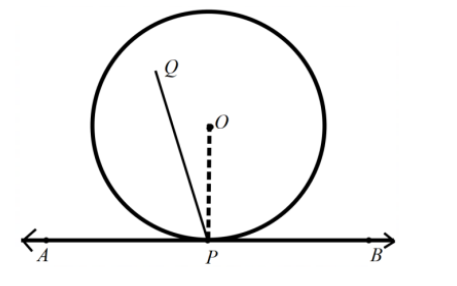
There can be two tangents drawn from the exterior point of a circle.
These definitions and rules have to be learnt properly and also practiced nicely to get the proper hold of the topic.
3. What are the topics learnt in Chapter 10 of Class 10 Maths?
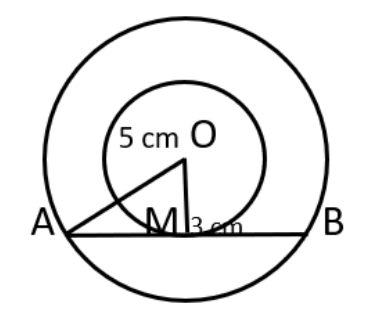
The Chapter 10 Circle of Class 10 Maths is very interesting. This chapter is an introduction chapter and the students will learn everything about circles, diameter, radius, tangents, secants, and theorems connected with these. These topics need thorough revision and students should practice till they get the concepts clear. Maths is a subject that cannot be memorized. The level of perfection can be only through practice.
4. How can the NCERT solutions of Vedantu help in the preparation of the chapter?
Since this is an introduction to the chapter, initially some students might take some time to understand the concepts and the theorems. Along with the textbook, you can refer to NCERT Solutions for Class 10 by Vedantu, which will be your best guide. You can practice various questions. This chapter has been explained very thoroughly in a simple way. The solutions are prepared by the experts so one can rely on them and start their board preparation with full confidence. The solutions can be availed for free both in Hindi and English and can be practised by visiting the w̱ebsite and Vedantu’s mobile app.
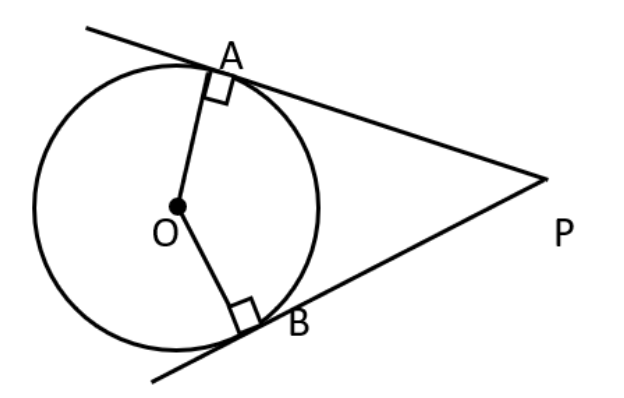
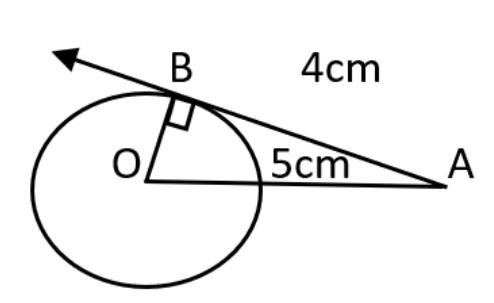
5. What are the number of tangents that can be drawn from a given external point?
From an exterior point to a given circle, two tangents can be drawn. The complete solution and explanation of the theorem is provided on Vedantu. The explanation is given in such an easy manner and crafted by experts that students will be able to grasp it easily. Right from important definitions to solutions and important questions, everything is available at Vedantu.
