Motion Questions and Answers - Free PDF Download
NCERT Solutions For Class 9 Science Chapter 7 Motion - 2025-26
FAQs on NCERT Solutions For Class 9 Science Chapter 7 Motion - 2025-26
1. Why are the NCERT Solutions for Class 9 Science Chapter 7 important for the 2025-26 exams?
The NCERT Solutions for Class 9 Science Chapter 7 are crucial as they provide the authoritative, step-by-step methodology for solving all in-text and exercise questions as per the latest CBSE 2025–26 syllabus. They help students understand the correct format for writing answers, including formulas, unit conversions, and final statements, which is essential for scoring full marks.
2. What is the best way to use the NCERT Solutions for solving problems in Chapter 7, Motion?
For effective learning, first attempt to solve the NCERT textbook problems on your own. Then, use the provided solutions to verify your answers and, more importantly, to understand the step-by-step method. Pay close attention to how concepts like acceleration, velocity, and displacement are applied, and analyse the steps where your method differed. This approach builds problem-solving skills rather than encouraging rote memorization.
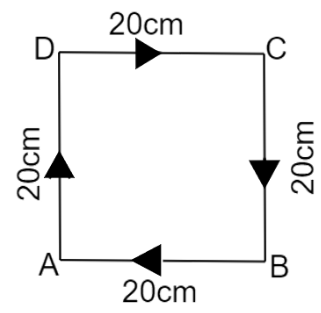
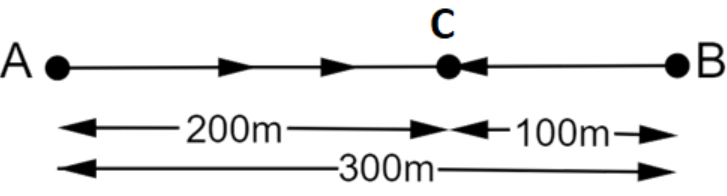
3. How do the NCERT Solutions explain the concept of zero displacement even when an object has travelled a distance?
The NCERT solutions explain this by breaking down the definitions. They clarify that distance is the total path length covered, while displacement is the shortest straight-line distance between the initial and final points. The solution for the example of an object moving in a circular path and returning to the start shows that while the distance is the circumference (2πr), the displacement is zero because the initial and final positions are the same.
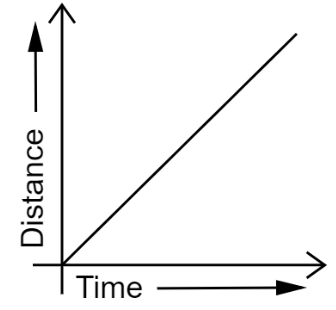
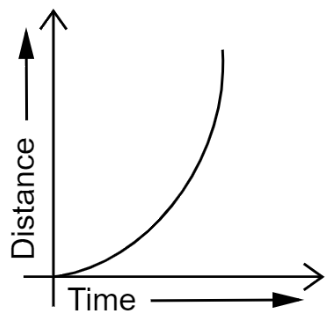
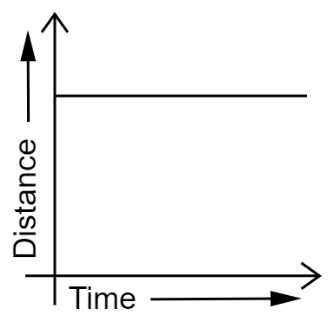
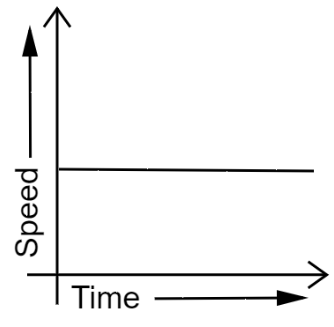
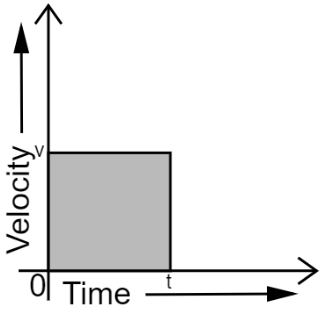
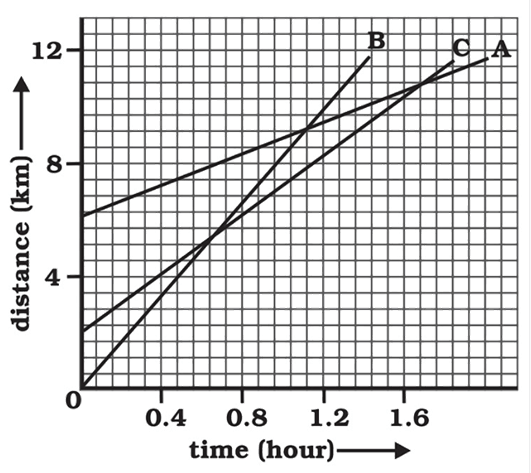
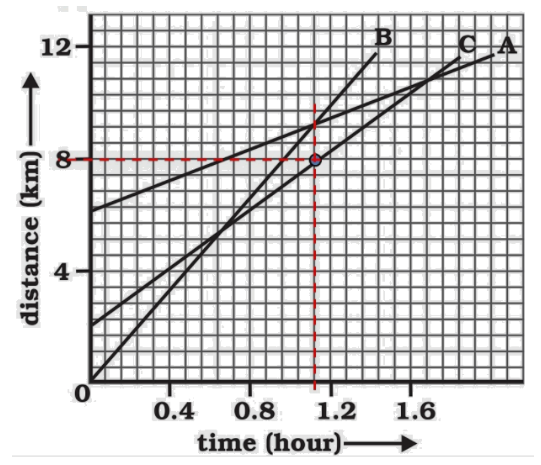
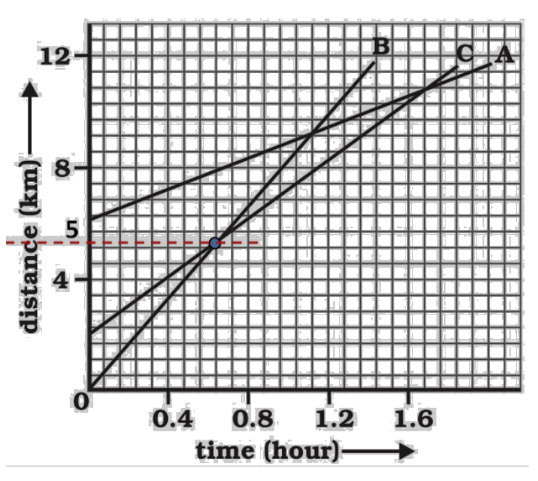
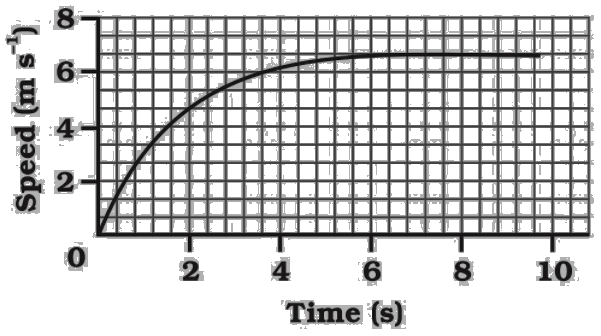
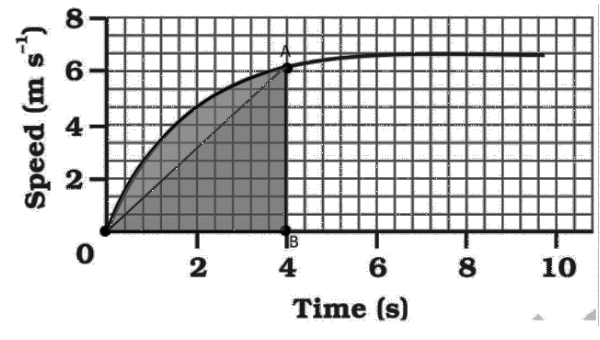
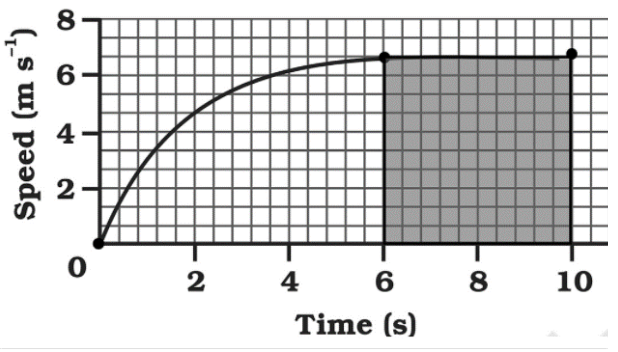
4. How are distance-time and velocity-time graphs used to solve numericals in the NCERT Class 9 Chapter 7 solutions?
The solutions demonstrate that graphs are powerful tools for solving motion problems. They show how to:
- Calculate an object's speed from the slope of a distance-time graph.
- Determine the distance travelled by calculating the area under a velocity-time graph.
- Identify the nature of motion (uniform, non-uniform, at rest) by interpreting the shape of the graph, such as a straight line or a curve.
5. How do the NCERT Solutions for Chapter 7 differentiate between speed and velocity?
The NCERT solutions clearly distinguish between speed and velocity by highlighting two key differences:
- Nature of Quantity: Speed is a scalar quantity, meaning it only has magnitude (e.g., 50 km/h). Velocity is a vector quantity, possessing both magnitude and direction (e.g., 50 km/h North).
- Calculation: Speed is calculated as total distance divided by time, whereas velocity is calculated as displacement divided by time. Because of this, velocity can be zero even when speed is not.
6. How should I correctly apply the sign conventions when solving numericals on acceleration from NCERT Chapter 7?
The NCERT solutions demonstrate a crucial rule: the sign depends on the direction of change in velocity. If an object's velocity is increasing in the direction of motion, the acceleration is positive. If the velocity is decreasing (like when brakes are applied), the acceleration is in the opposite direction and is considered negative. This negative acceleration is also known as retardation or deceleration, a key concept for solving problems accurately.
7. Many students confuse average speed and average velocity. How do the solved problems in NCERT Solutions for Chapter 7 (like the 'Abdul's trip' problem) clarify this difference?
The 'Abdul's trip' problem is a perfect illustration. The solution shows that to find average speed, you must calculate the total distance (to school and back) and divide it by the total time taken. However, to find average velocity for the entire trip, the displacement is zero (since Abdul returns to the starting point), making the average velocity zero. This example powerfully demonstrates that average speed depends on the entire path, while average velocity only depends on the start and end points.
8. The NCERT solutions for Chapter 7 include problems on uniform and non-uniform acceleration. Why is understanding the solution method for both types important?
Understanding both is vital because they describe different, realistic motion scenarios. The solutions for uniform acceleration problems use the three equations of motion (e.g., v = u + at), which apply only when acceleration is constant. In contrast, problems involving non-uniform acceleration, often represented by curved graphs, require a conceptual understanding that velocity changes by unequal amounts in equal time intervals. The solutions teach you to first identify the type of acceleration before choosing the correct formula or graphical method.
9. When solving problems involving the three equations of motion, what is a common mistake and how do the NCERT Solutions help prevent it?
A very common mistake is incorrect unit conversion. For example, students often forget to convert speed from km/h to m/s before using it in equations where time is in seconds. The NCERT solutions consistently show the conversion step (e.g., multiplying km/h by 5/18 to get m/s) right at the beginning of the solution. Following this structured approach, as shown in the solutions, helps build a habit of checking units first, preventing major errors in the final answer.
10. The NCERT solutions cover both linear and circular motion problems. What fundamental principle connects the solutions for a car moving on a straight road and an artificial satellite in orbit?
The connecting principle is the concept of velocity. For the car on a straight road, a change in velocity often means a change in speed. For the satellite in a circular orbit, the solutions highlight a more subtle point: even if the speed is constant, the direction of motion is continuously changing. This change in direction means the velocity is changing, which implies the satellite is constantly accelerating towards the centre of the orbit. The solutions thus teach that acceleration isn't just about speeding up or slowing down.




















 Watch Video
Watch Video